11. Методические рекомендации к проведению урока. Вариант 111. Методические рекомендации к проведению урока. Вариант 1

Методические рекомендации к проведению урока

Цель обучения: 6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений;

Критерии оценивания:

-понимает условие текста задачи;

-по условию задачи вводит новую переменную;

-правильно составляет уравнение;

-правильно вычисляет;

-правильно определяет решение.

Организационный момент. Актуализация знаний. Ознакомьте учащихся с целями урока и ожидаемыми результатами.  

Для актуализации знании предложите учащимся устную работу.

Каждый ряд получает карточку для устной работы Учащиеся решают линейные уравнения “по цепочке”, вписывают буквы в соответствующий столбец.

По окончании работы проверяются её результаты.

Объясните учащимся, что получившиеся слова (интеграл, логарифм, экспонента) – это математические термины, с которыми школьники познакомятся в старших классах.

Проведите формативное оценивание в виде смайликов или фишек.

1 ряд.

Найдите устно корни каждого уравнения и впишите в третий столбец соответствующие им буквы.

Таблица выбора ответов:

2 ряд.

Найдите устно корни каждого уравнения и впишите в третий столбец соответствующие им буквы.

Таблица выбора ответов:

3 ряд.

Найдите устно корни каждого уравнения и впишите в третий столбец соответствующие им буквы.

Таблица выбора ответов:

Изучение новой темы: Предложите учащимся решить текстовую задачу, предварительно составив уравнение.Из двух городов, расстояние между которыми 500 км, одновременно навстречу друг-другу выехали трактор и грузовик. Скорость грузовика в 4 раза больше скорости трактора. Они встретились через 4 часа.Какая скорость трактора?

Решение: Пусть скорость трактора х (км/час), тогда скорость грузовика будет 4х (км/час).

Тогда по условию задачи составим следующее уравнение:

  Отсюда

Значит,скорость  трактора 25 км/час.

Совместно с учащимися составьте Основные этапы решения текстовой задач :

1.неизвестную величину, значение которой мы хотим определить, обозначаем буквой, например x;
2.используя эту букву и имеющиеся в задаче данные, составляем математическую модель, где два разных выражения равны друг другу;
3.записывая эти выражения через знак равно, мы получаем уравнение, решение которого 

поможет найти ответ к задаче; 
4.если необходимо, выполняем дополнительные действия для нахождения ответа к задаче. 

Проведите гимнастику для глаз.

Объедините учащихся в группы. Используйте метод «Карусель» – работа в группах сменного состава.

Предоставьте ресурс с четырьмя задачами разной тематики, решаемых алгебраическим способом. На первом этапе работы, учащиеся разделяют задания в группе между собой. На втором этапе, формируются новые группы учащихся по выбранным заданиям. Объединившись в группы, которые решают одни и те же задания, учащиеся обсуждают, находят решения, осуществляют запись, приходят к полному пониманию решения. На третьем этапе, учащиеся возвращаются в группы исходного состава и объясняют в группе решение своей задачи.

ПРАКТИЧЕСКАЯ РАБОТА ( Метод Карусель)

Составьте уравнения по условиям данных задач:

№ 1.  Автомашина за 3,5 ч проехала на 10 км больше, чем мотоцикл за 2,5 ч. Скорость мотоцикла на 20 км/ч больше, чем скорость автомашины. Найдите скорость автомашины и скорость мотоцикла.

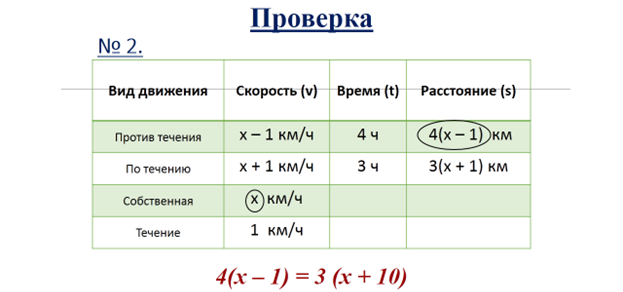
№ 2.  Лодка проплыла от одной пристани до другой против течения реки за 4 ч. Обратный путь занял у нее 3 ч. Скорость течения реки 1 км/ч. Найдите собственную скорость лодки и расстояние между пристанями.

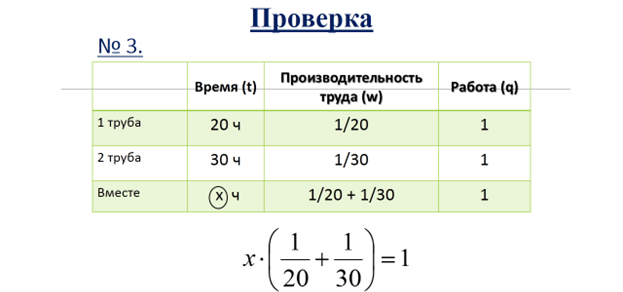
№ 3. Через первую трубу бассейн можно заполнить за 20 ч, а через вторую - за 30 ч. За сколько часов наполнится бассейн через обе эти трубы?

№ 4.  Чтобы выполнить задание в срок, токарь должен был изготавливать по 24 детали в день. Однако он ежедневно перевыполнял норму на 15 деталей сверх плана и уже за 6 дней до срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?

Учащиеся отвечают на вопросы рефлексии:

-        Что сегодня я узнал?

-        Мне было тяжело или нет?

-        Я понял материал или были затруднения?

-        Я научился чему-то новому?

-        Я смог добиться результата?

Ресурсы:

1.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.      Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

3.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

4.       Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.