16Основные правила комбинаторки. Факториал. Дидактический материал

Задания

1.Сколькими способами можно составить пару из одной гласной и одной согласной букв слова «платок»?

гласные: а, о – 2 шт.

согласные: п, л, т, к – 4 шт.

                   2 • 4 = 8

Ответ: 8 способами.

2.Сколько танцевальных пар можно составить из 8 юношей и 6 девушек?

                    6 • 8 = 48

Ответ: 48 пар.

3. В столовой есть 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать?

                             4 • 7 = 28

Ответ: 28 вариантов.

4. Сколько различных двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры могут повторяться?

Решение:    1 цифра – 3 способа

                    2 цифра – 3 способа

                    3 цифра – 3 способа

                            3 • 3 = 9

                        Ответ: 9 различных двузначных чисел.

5. Сколько различных трёхзначных чисел можно составить, используя цифры 3 и 5, если цифры могут повторяться?

Решение: 1 цифра – 2 способа

                 2 цифра – 2 способа

                 3 цифра – 2 способа

                 2 • 2 • 2 = 8

                      Ответ: 8 различных чисел.

6.  В семье – шесть человек, а за столом в кухне – шесть стульев. В семье решили  каждый вечер, ужиная, рассаживаться на эти шесть стульев по-новому. Сколько дней члены скмьи смогут это сделать без повторений?

Решение:

Для удобства будем считать , что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться поочередно.

У бабушки – 6 вариантов выбора стульев.

У дедушки – 5 вариантов выбора стульев.

У мамы – 4 варианта выбора стульев.

У папы – 3 варианта выбора стульев.

У дочери – 2 варианта выбора стульев.

У сына – 1 вариант выбора стульев.

По правилу умножения: 6×5×4×3×2×1 = 720 (дней).

7. Имеется десять различных книг, три из которых - справочники. Сколькими способами можно расставить эти книги на полке так, чтобы все справочники стояли рядом?

Решение: Так как справочники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 – 3 + 1 = 8 книг. Это можно сделать 8! способами. Для каждой из полученных комбинаций можно сделать Р3 перестановок справочников. Поэтому число способов расположения книг на полке равно произведению:  8! · 3! = 40 320 · 6 = 241 920.

8.  Вычислите:

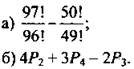
9.  Вычислите:

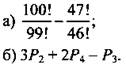
10. Упростите:      a) n! /(n+1)!;                б) n!/(n-2)!;

                                в) (n+1)!/(n-2)!;           г) n!/(n-k)! , n>k

11.  Упростите:

а) 1/(n+1)! – 1/(n+2)!;                           б) n!/(n+1)! – (n-1)!/n!

 в) (n-1)!/n!                                            г) n!/(n-3)!   

12. Упростите:

а) 1/k! – 1/(k+1)!                                   б) (n-2)!/n! – n!/(n+1)!

в) (n-2)!/(n-4)!                                       г) (n+1)!/(n-k+1)! , n>k

13. Решите уравнение:

а) (n+2)!/n! = 72                                    б) (n+1)!/(n-1)! = 30

14. Вычислите:

а) (P₅+P₄)/P₃                     б) (P₁₀ - P₉)/9P₈                              в) P_3k/P_(3k-2) 

№15. Вычислите :

а) (P₆+P₅)/P₄                     б) (P₁₂ – P₁₁)/11P₁₀                     в) P_(3k+2)/P_(3k+1)