1Бесконечно убывающая геом прогр (1)

Знакомимся с новыми знаниями

Если несколько чисел образуют геометрическую прогрессию, то среди них всегда найдётся наименьшее по модулю число; если же чисел, образующих геометрическую прогрессию, бесконечно много, то наименьшее по модулю число найдётся не всегда.
Можно доказать, что наименьшего по модулю числа нет только в так называемых бесконечно убывающих геометрических прогрессиях, к изучению которых мы и приступаем.

Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше 1: .

 

Пример 1. Геометрическая прогрессия

бесконечно убывающая, так как:

.

.

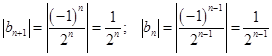Докажем теперь, что в любой бесконечно убывающей геометрической прогрессии модуль любого члена прогрессии меньше модуля последующего члена прогрессии.

Действительно, пусть прогрессия задана формулой .

Тогда

, так как .

Теперь поработаем с формулой суммы первых n членов бесконечно убывающей геометрической прогрессии. Перепишем её в виде:

 Можно доказать, что при неограниченном увеличении n выражение

не просто уменьшается по модулю, что мы уже фактически доказали выше, а стремится к нулю. Тогда левая часть равенства стремится к S, где

.

Получили следующий результат.

Сумма бесконечно убывающей геометрической прогрессии равна: .

 

Пример 2. Найдём сумму бесконечно убывающей геометрической прогрессии

.

Воспользуемся формулой:

Получим:

.

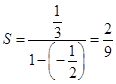Как нам известно, рациональные числа представимы в виде бесконечных периодических десятичных дробей. Перевести бесконечную периодическую десятичную дробь в обыкновенную можно, используя формулу суммы бесконечно убывающей геометрической прогрессии.

Пример 3. Запишем дробь 0,(15) в виде обыкновенной дроби.

Данную бесконечную периодическую десятичную дробь можно представить в виде суммы бесконечно убывающей геометрической прогрессии, первый член которой равен b₁ = 0,15, а знаменатель q = 0,01:

0,(15)  =  0,151515… =  0,15 + 0,0015 + 0,000015 + ... .

Воспользуемся формулой:

.

Поличим:

.

Пример 4. Запишем дробь 0,4(1) в виде обыкновенной дроби.

Представим бесконечную десятичную дробь в виде:

0,4(1) = 0,4 + 0,01 + 0,001 + ... .

Данную периодическую десятичную дробь можно представить в виде суммы числа 0,4 и бесконечно убывающей геометрической прогрессии, первый член которой равен b₁ = 0,1, а знаменатель q = 0,1.

Получим:

.

Ответ: .

 

 

 

 

 

Литература:

Федеральный государственный образовательный стандарт
Образовательная система «Школа 2100»
А.Г. Рубин, П.В. Чулков
АЛГЕБРА
9 класс

Москва
2015