1Элементы теорий вероятности_дидактический материал

1-группа.

При бросании двух монет покажите различные возможности исходов события разными способами. 

а) с помощью краткой записи: ГГ, ГЧ, ЧГ, ЧЧ.

б) двухмерного пространства:

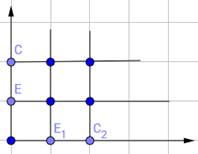
в) дерева возможностей:

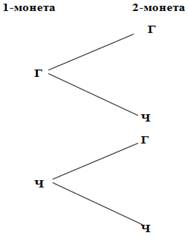
Теперь учащиеся могут находить вероятность, например: видно, что вероятность выпадения герба в обоих монетах равно или вероятность выпадения герба в одной из них равно , так как количество всех равновозможных исходов 4, а благоприятствующих 2.

2-группа.

На гранях игральной кости отмечены числа 0, 0, 1, 1, 4 и 5. Если она была подрошена два раза, то вычислите вероятность того, что

а) сумма ее сторон равна 5;

б) оба раза выпали одинаковые числа. 

Покажите что, в данном задании удобнее будет использовать двухмерное пространство:

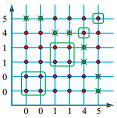
Ответ: а)  ; б) .

3-группа.

Вспомним раздел «Теория множеств», который мы прошли в 1 четверти, и попробуем с ее помощью найти вероятность случайного события. 

В классе всего 30 учащихся. 19 из них занимаются спортом, а 8 играют на пианино, 3 учащихся занимаются спортом и играют на пианино. Представьте данную информацию с помощью диаграммы Эйлера-Венна и найдите вероятность того, что наудачу выбранный ученик:

а) занимается спортом и играет на пианино;

б) занимается спортом или играет на пианино;

в) занимается спортом, но не играет на пианино;

г) либо занимается спортом, либо играет на пианино;

д) не занимается спортом и не играет на пианино;

е) играет на пианино если известно, что он занимается спортом.

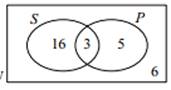
Ответ: а) ; б) ; в) ; г) ; д) ; е)  (если мы знаем, что учащийся занимается спортом, тогда рассматривается только среди этих учащихся играющие на пианино).

Примеры решений на классическую вероятность

Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?

Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. Событие А достоверное.

Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?

Решение. Вынуть два шара из десяти можно следующим числом способов: 

. 
Число случаев, когда среди этих двух шаров будут два белых, равно     . 
Искомая вероятность    
.

Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Решение. Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. Событие, заключающееся в вынимании синего шара, невозможное.

Пример. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?

Решение. Количество элементарных исходов (количество карт) n=36. Событие А = (Появление карты червовой масти). Число случаев, благоприятствующих появлению события А, m=9. Следовательно,
.

Задача 1: Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.

Решение: Вероятность набрать верную цифру из десяти равна по условию 1/10. Рассмотрим следующие случаи: 
1. первый звонок оказался верным, вероятность равна 1/10 (сразу набрана нужная цифра).
2. первый звонок оказался неверным, а второй - верным, вероятность равна 9/10*1/9=1/10 (первый раз набрана неверная цифра, а второй раз верная из оставшихся девяти цифр).
3. первый и второй звонки оказались неверными, а третий - верным, вероятность равна 9/10*8/9*1/8=1/10 (аналогично пункту 2).

Всего получаем P=1/10+1/10+1/10=3/10=0,3P=1/10+1/10+1/10=3/10=0,3 - вероятность того, что ему придется звонить не более чем в три места.

Ответ: 0,3

Задача 2: Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.

Решение: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов. 
m=1m=1, так как только одно число правильное. Подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент:

Таких чисел n=18n=18 штук. Тогда искомая вероятность P=1/18P=1/18. 

Ответ: 1/18.

Задача 3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.

Решение: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

m=6m=6, так как есть только три случая расположения 6 шаров по 3 ящикам, чтобы во всех ящиках оказалось разное число шаров: (1, 2, 3), (2, 1, 3), (3, 2, 1), (1, 3, 2), (2, 3, 1), (3, 1, 2).

Всего случаев расположения 6 шаров по 3 ящикам, чтобы ни один ящик не остался пустым равно 

Тогда искомая вероятность P=6/10=0,6.

Ответ: 0,6.

Задача 4: На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую?

Решение: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

Число всех способов расставить ладьи равно n=64⋅63=4032n=64⋅63=4032 (первую ладью ставим на любую из 64 клеток, а вторую - на любую из оставшихся 63 клеток).

Число способов расставить ладьи так, что они не будут бить одна другую равно m=64⋅(64−15)=64⋅49=3136m=64⋅(64−15)=64⋅49=3136 (первую ладью ставим на любую из 64 клеток, вычеркиваем клетки, которые находятся в том же столбце и строке, что и данная ладья, затем вторую ладью ставим на любую из оставшихся после вычеркивания 49 клеток).

Тогда искомая вероятность P=3136/4032=49/63=7/9=0,778.P=3136/4032=49/63=7/9=0,778.

Ответ: 7/9.

Задача 5. Шесть рукописей случайно раскладывают по пяти папкам. Какова вероятность того, что ровно одна папка останется пустой?

Решение: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

Подсчитаем - число различных способов разложить 6 рукописей по 5 папкам, причем в каждой папке может быть любое количество рукописей.

Теперь подсчитаем  - число способов разложить 6 рукописей по 4 папкам, причем в каждой папке должно быть не менее одной рукописи. При этом нужно полученное число сочетаний умножить на 5, так как папку, которая останется пустой, можно выбрать 5 способами.

Искомая вероятность Р=50/210=5/21.Р=50/210=5/21.

Ответ: 5/21.

Задача 7. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.

Решение: Используем классическое определение вероятности: P=m/nP=m/n, где nn - число всех равновозможных элементарных исходов, mm - число элементарных исходов, благоприятствующих осуществлению события AA = (Тома стоят в порядке возвозрастания номера слева направо, но не обязательно рядом). 

n=40⋅39⋅38=59280n=40⋅39⋅38=59280, так как первый том можно поставить на любое из 40 мест, второй - на любое из 39 мест и третий - на любое из оставшихся 38 мест. А число

Тогда искомая вероятность  

Ответ: 1/6.

Скачано с www.znanio.ru