
Формативная работа.
Уровень А
1. Сколько различных четырехзначных чисел можно составить из цифр 2, 4, 6, 7 так, чтобы все цифры участвовали в записи?
а) 4; б) 720; в) 24; г) 23.
2.Сколько различных четных четырехзначных чисел можно составить из цифр 1, 3, 5, 8 так, чтобы все цифры участвовали в записи?
а) 24; б) 18; в) 6; г) 12.
3.Сколько различных четырехцветных флагов из четырех полос можно получить, если можно использовать 5 цветов?
а) 20; б) 120; в) 60; г) 720.
4.В классе 20 учеников. Сколькими способами можно выбрать из них троих дежурных? Задачу можно решить по формуле:
а)числа перестановок из трех элементов; б)числа размещений из 20 элементов по три; в) числа перестановок из 20 элементов; г) числа сочетаний из 20 элементов по три


![]()


Формативная работа.
УровеньВ
1.Сколько различных сигналов из 9 символов можно передать так, чтобы три первых символа не менялись?
а) 27; б) 18; в) 6!; г) 9!.
2.Сколькими способами можно расставить на полке 6 книг, если среди них есть двухтомник, книги которого должны стоять рядом?
а) 720; б) 4; в) 15; г) 120.
3. В классе 25 учащихся. Сколькими способами можно выбрать из них
трех делегатов на конференцию а) ![]() ; б)
; б)![]() ; в) 75; г)
; в) 75; г) ![]() .
.
4. Сколько различных четырехцветных флагов из четырех полос можно получить, если можно использовать 5 цветов, при этом два из этих цветов (синий и красный) должны быть рядом?
а) 24; б) 72; в) 60; г) 48 .
![]()
![]()
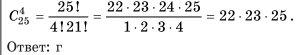

Формативная работа.
УровеньС
1. Сколько различных четырехзначных чисел можно составить из цифр 2, 8, 9, 0 так, чтобы все цифры участвовали в записи?
а) 24; б) 18; в) 4; г) 15 .
2. Сколькими способами можно составить пятизначное число из цифр 1, 2, 3, 4, 5 так, чтобы в нем на первом месте стояла цифра 4, а цифры 3 и 5 стояли рядом?
а) 24; б) 18; в) 12; г) 120.
3.В подразделении 60 солдат и 5 офицеров. Сколькими способами можно выбрать из них четырех солдат и двух офицеров для несения караула?
а) 385; б) 25 • 57 • 58 • 59 ; в) 57 • 58 • 59 ; г) 2 • 604.
4.Сколько различных четырехцветных флагов из четырех полос можно получить, если можно использовать 5 цветов, при этом два из этих цветов (синий и красный) не должны быть рядом?
а) 20; б) 72; в) 60; г) 720 .



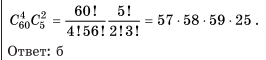
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.