21.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.5.1.7 решать текстовые задачи с помощью составления систем линейных уравнений;

Критерии оценивания:

- вводит переменные и составляет математическую модель текстовой задачи;

-решает систему уравнений;

 Организационный момент. Приветствие. Отметка отсутствующих. Проверка готовности учащихся к уроку.Совместно с учащимися определяем цели урока и ожидаемые результаты. Разбор домашнего задания. Учащиеся обмениваются домашним заданием и выполняют проверку по готовым решениям.

 Повторение пройденного материала проведите с помощью метода: «Отпусти с мелом». Подготовьте список вопросов. Выдайте одному ученику мел и перечисляйте вопросы. Ученик с мелом в руках, выбирает любой вопрос из списка на листочке и отвечает на нее. Когда ученик отвечает на вопрос, мел может быть передан любому ученику по его усмотрению.

Перечень вопросов:

-Что называют решением системы?

-Что значит решить систему уравнений?

-Сформулируй алгоритм решения системы методом подстановки.

-Сформулируй алгоритм решения системы уравнений методом алгебраического сложения.

Проведите устное формативное оценивание. За каждый правильный ответ – смайлик или фишку.

Дескриптор:

-вводит переменные и составляет математическую модель текстовой задачи;

-решает систему уравнений;

-верно записывает ответ;

 Для отработки навыков применения действий над рациональными числами предложите учащимся дидактическую игру «Мешочек задании». Подготовьте карточки с заданиями по теме «Решение систем линейных уравнении с помощью метода подстановки и методом алгебраического сложения». Разрежьте карточки и сложите в «мешочек» (контейнер). Разделите учащихся на пары, каждая пара достает из «мешочка» карточку с заданием, осуществляет решение, комментируя его. Остальные пары осуществляют проверку.

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.

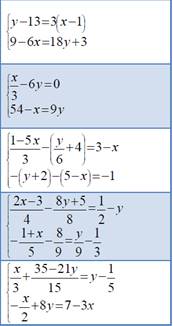
Ответ:

Проведите физкультминутку для учащихся:

Дружно с вами мы считали и про числа рассуждали,

А теперь мы дружно встали, свои косточки размяли.

На счет раз кулак сожмем, на счет два в локтях согнем.

На счет три — прижмем к плечам, на 4 — к небесам,

Хорошо прогнулись, и друг другу улыбнулись.

Про пятерку не забудем — добрыми всегда мы будем.

На счет шесть прошу всех сесть.

Закрепление темы с помощью прием «Автобусная остановка».

Цель: Принимать во внимание чужие идеи, целостно обсудить тему или вопрос, активно и пассивно.

Организация: Подготовьте задания для серии станций: «Задачи на движение», «Задачи на работу», Задачи на движение по реке», «Задачи на числа», подготовьте для групп флипчарты, раздайте группе разноцветные карандаши – поэтому нужно следить кто что нарисовал).

Как это работает: Разместите каждую малую группу на станции, дайте 3-4 минут обсудить задание и записать их мысли на бумаге или доске. По истечению времени, группа перемещается к другой станции, где группа продолжает работу предыдущей группы. Перемещение происходит каждые минут, пока каждая группа не побывала на каждой позиции и обдумала мысли всех групп.

Задачи на движение:

1.Туристы сначала плыли на теплоходе 2 ч, а затем шли 5 ч пешком до конечного пункта. Известно, что по реке они проплыли в 3 раза больше расстояние, чем прошли пешком. Найдите скорости туристов и теплохода, если известно, что скорость теплохода на 26 км/ч больше скорости туристов. Сколько времени понадобилось бы туритсам, чтобы пройти весь путь пешком.

2.Путь от туристической базы до моря пролегал сначала в гору, а затем  с горы. От турбазы до моря туристы шли в гору 45мин и с горы 40мин, а обратно в гору 1час15мин, а с горы 24 мин. Найдите длину каждого участка пути, если путь в одну сторону равен 6,4км.

Решение:

1.     

2.     

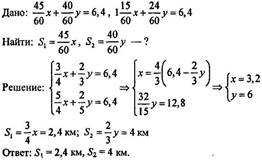
Задачи на движение по реке.

1.Моторная лодка за 3 часа движения против течения реки и 2,5 ч по течению реки проходит 98 км. Найдите собственную скорость лодки и скорость течения, если за 5 ч движения по течению она проходит на 36 км больше, чем за 4 ч против течения реки.

Решение:

Задачи на работу.

Два фрезеровщика один из которых работал 5 дней, а другой -8 дней изготовили 280 деталей. Затем, применив новую фрезу, первый повысил производительность труда на 62,5 %, а второй – на 50%, и уже за 4 дня совместной работы они изготовили 276 деталей. Сколько деталей изготовили бы они с новой фрезой, если бы, как и раньше, первый работал 5 дней, а другой -8 дней.

Решение:

Задачи на числа.

1.Найдите два числа, если их разность равна 23, а сумма удвоенного большего из этих чисел и второго числа равна 22.

            2. Представьте в виде многочлена и упростите:

            3. Представьте в виде многочлена и упростите:

Решение.

1.Пусть I (большее) число -х, тогда II число - у. По условию  х-у=23, а 2х+у=22. Составим и решим систему уравнений:

Ответ: 15 и -8 – искомые числа.

2.

3.

Дескриптор:

-вводит переменные и составляет математическую модель текстовой задачи;

-решает систему уравнений;

-верно записывает ответ;

Рефлексия.

Подведение итогов урока.

В конце урока учащиеся проводят рефлексию:

Домашнее задание: № 1635 стр.388

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Джумагуловы.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.

3. А.Г.Мордкович. Алгебра. Задачник 7 класс. Изд. Мнемозина. Москва.2010 год.