22. Решение СЛУ с двумя переменными способом подстановки Метод

Методические рекомендации к уроку

Тема урока " Решение системы линейных уравнений с двумя переменными способом подстановки "

Цели обучения:

6.2.2.19

решать системы уравнений способом подстановки и способом сложения;

Критерии оценивания

Учащиеся

знают:

как решать системы уравнений способом подстановки.

умеют

решать системы уравнений способом подстановки.

Теоретический материал

Алгоритм решения системы двух уравнений с двумя переменными x,y
способом подстановки:

1. Выразить одну переменную через другую из одного уравнения системы (более простого).

2. Подставить полученное выражение вместо этой переменной в другое уравнение системы.

3. Решить полученное уравнение и найти одну из переменных.

4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения в уравнение, полученное на первом шаге и найти вторую переменную.

5. Записать ответ в виде пар значений, например, (x;y), которые были найдены соответственно на третьем и четвёртом шаге.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Устно: В заданном уравнении выразите одну переменную через другую:

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. В режиме диалога вспомнить способ решения подстановкой системы двух уравнений, когда необходимо предварительно упростить уравнения, затем выбрать более простое уравнение из которого выразить одну переменную через другую. В следующих системах необходимо предварительно перейти к целым коэффициентам, затем действовать по алгоритму.

Приложение 1

Задание 1. Решите систему уравнений способом подстановки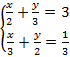  

Решение: 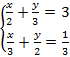             Умножим каждое уравнение на общий знаменатель дробей 6, чтобы перейти к целым коэффициентам, затем действовать по алгоритму

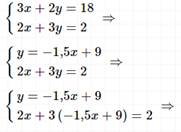
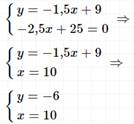              Ответ: (10; -6).

Задание 2. Решите систему уравнений способом подстановки

Решение: . Умножим первое уравнение на общий знаменатель дробей 6, чтобы перейти к целым коэффициентам, затем действуем по алгоритму.

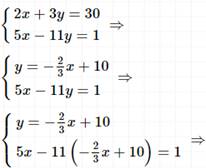
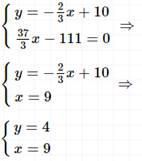                               Ответ: (9;4)

При выполнении задания можно использовать прием «Активный класс». Пригласите к доске 4 учащихся попросите их записать подробное решение 1-4 соответственно. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого примера.

Учащиеся решают, показывая подробное решение на доске.

Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они

могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса

Учащиеся формулируют определения, сравнивают с текстом учебника, делают выводы.

Первичное закрепления знаний. Выработка умений решать задания по теме.

Задание 3

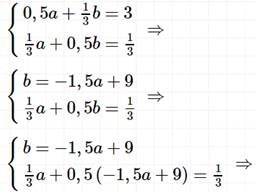
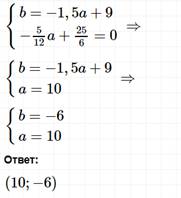
Работа в парах. Взаимное обучение. Создать пары из представителей разных групп. Предложить ученикам процесс взаимного обучения: объяснить напарнику ход решения задания, затем вместе решить их. Определяем умение распределять обязанности в паре.

Приложение 2

Задание 1

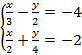
Решение: Умножим первое уравнение на общий знаменатель дробей 6, а второе уравнение на общий знаменатель дробей 4, чтобы перейти к целым коэффициентам в уравнениях, затем действовать по алгоритму.

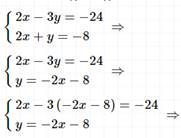
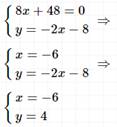              Ответ: (-6; 4).

Задание 2

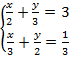
Решение: Умножим первое и второе уравнение на общий знаменатель дробей 6, чтобы перейти к целым коэффициентам в уравнениях, затем действовать по алгоритму.

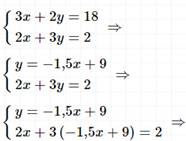
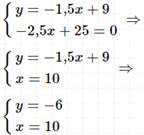 Ответ: (10; -6).

Предоставить достаточно времени для выполнения задания.

Подвести итог после решения этих заданий.

Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Беседа. Рефлексия.

Вопросы учащимся:

1. Что называется решением системы двух уравнений с двумя переменными?

2. Что значит решить систему уравнений?

3. Как проверить, является ли данная пара решением системы?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.                  "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.                  "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.                  Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.                  Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.                  Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.                  http://www.yaklass.ru

2.                  https://school-assistant.ru