28. Целые числа. Рациональные числа. Приложение 2. Вариант 2

Приложение 2 (теория)

Множества обычно обозначают большими буквами латинского алфавита: А, В,  С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных  разделах математики, что для них ввели специальные обозначения:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

I – множество иррациональных чисел;

R – множество действительных чисел.

Чтобы не забыть, что перечисляемые элементы объединены вместе в  некоторое множество, такое перечисление производят внутри фигурных скобок {,}.

Например, цифры десятичной системы счисления задаются множеством

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.

Элементы множества можно перечислять в произвольном порядке. От изменения порядка   перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается {А, Е, Ё, И, О, У, Ы, Э, Ю, Я} или {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.

Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.

{А, Е, Ё, И, О, У, Ы, Э, Ю, Я} = {Э, Е, А, Ё, Я, О, Ы, И, У, Ю}.

Чтобы задать конечное множество, можно просто перечислить все его элементы.

Например, запись А = {2; 3; 5; 7; 11; 13} означает, что множество А состоит из первых шести простых чисел.

Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.

Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать {1; 4; 9; 16; 25; …}, а множество всех чисел, которые больше 5 и меньше 12 записать {х | 5< х <12} или (5; 12). В примерах использован оборот “ … и так далее” и символ “ | ” внутри фигурных скобок заменяющий комбинацию слов “ … таких, что …”. (Множество всех х таких, что 5< х <12).

Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных случаях множество называют пустым и обозначают символом Æ, в фигурные скобки его не ставят, так как никакого перечисления элементов пустого множества не происходит.

Словесные обороты, как “элемент х принадлежит множеству А” или “х – элемент множества А”, достаточно длинны и не всегда удобны в записи решений конкретных задач.

В математике эти выражения кратко записывают так: х  А, где  – знак принадлежности.

Например, 5N, лучше читать не буквально, а в “литературном переводе”, “5 – число натуральное”. Наряду со знаком принадлежит используют и его “отрицание” – знак  (знак не принадлежит). Запись 0 N означает, что нуль не натуральное число.

Возьмем множество А = {2; 4; 6} и В = {1; 2; 3; 4; 5; 6; 7}. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.

Знак “” называют знаком включения.

Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера (Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).

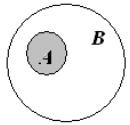
Рис. 1

Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств  взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).

Из данных множеств с помощью специальных операций можно образовывать новые множества:

1) Пересечением множества А и В называют множество, состоящие из всех общих 11элементов множеств А и В, т. е. из всех элементов, которые принадлежат и множеству А, и множеству В (рис. 2). Пересечение множеств А и В обозначают так: АВ. Это определение можно записать и так: АВ = {х | х  А и х  В}. Иными словами, пересечение двух множеств – это их общая часть. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АВ = {3; 9}. Если А = {10; 20; …90; 100} и В = {6; 12; 18;…}, то АВ = {30; 60; 90}. Можно рассматривать пересечение не только двух, но трех, четырех и т. д. множеств. Пересечение множеств В, С и D обозначают так: ВСD.

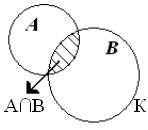
Рис. 2

2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.

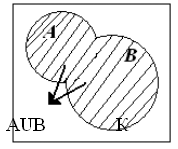
Рис. 3

Это определение можно записать и так: АUВ = {х | х  А или х  В}. Например, если А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то АUВ = {1; 3; 5; 7; 9; 11; 12}. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.