29. Модуль числа. Методические к уроку. Вариант 2

Методические рекомендации к уроку

Тема урока "Модуль числа "

Цели обучения:

6.1.1.9

знать определение модуля числа и находить его значение;

6.2.1.11

понимать геометрический смысл выражения ;

6.3.3.1

находить расстояние между точками на координатной прямой;

Критерии оценивания

Учащийся:

знает:

·         определение модуля числа;

·     геометрический смысл выражения ;

умеет:

·         находить значение модуля числа;

·         находить расстояние между точками на координатной прямой;

·         применять  при решении задач.

Теоретический материал (Приложение 1)

Расстояние от начала отсчета до точки, обозначающей данное число, называют модулем этого числа(от латинского modus -мера, величина).

Модуль числа а обозначается символом . Например,

,

Взаимно противоположные числа расположены на координатной прямой по разные стороны от 0 на одинаковом расстоянии от него. Так, числа 2 и (-2) оба расположены на расстоянии 2 единиц от 0, а числа (-4,5) и 4,5 - на расстоянии 4,5 от 0. Полученные точки попарно симметричны относительно начала отсчета на координатной прямой.

Так как противоположные числа находятся на одинаковом расстоянии от начала отсчета, то их модули равны:

Модуль числа 0 считается равным 0: это число находится на "нулевом расстоянии" от самого себя:

Как и любое расстояние между двумя точками, модуль не может быть отрицательным. Таким образом, для любого числа а выполняется неравенство:

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание:

Какие числа называются противоположными?

1. Среди данных чисел укажите пары противоположных чисел:

2. а) Найдите значения выражения:

-(-(-(-1)));    -(-(-1));       -(-(-(-(-1))))

б) Найдите значения выражения:

-(-с), если с=2,3 ; -4¼

-(-(-а)), если а = -12,3 ;  7½

в) Каким будет число: –в, если в – отрицательное число; в=0; в – число положительное.

Совместно с учащимися определить тему и цели урока, зону ближайшего развития.

Коллективная работа. Решите уравнения:

1.  -(-(-х) = -1

       -х = -1

         х = 1          

2.   -х = 0

        х = 0

3.   - (-(-(-х) = 4

       х = 4

4.   -а = -4

       а = 4

Предложить учащимся решить задачу, ответив на вопросы, сделать вывод.

Задача. Девочки вышли  из пункта О, двигаясь по прямой, им надо пройти путь в 6 км (1км = 1 ед.отрезку). В какую точку они попадут? Как надо двигаться, чтобы попасть в эти точки? (в противоположных направлениях) Сколько километров прошла каждая девочка?

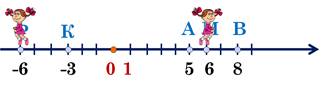
Совместно с учащимися определите: где должны находится эти точки?

От точки P(−6) до нуля и от точки M(6) до нуля равно 6 единичных отрезка.

Учитель вводит новый термин: Это расстояние называют модулем. Выполнив задание, учащиеся высказывают гипотезы об определении модуля, используя слово «модуль» и «расстояние». Выводят совместно с учителем определение.

Определение: Расстояние от начала отсчета до точки, обозначающей данное число, называют модулем этого числа (от латинского modus -мера, величина).

Число 6 является модулем числа −6 и числа 6.

Ввод обозначения. Модуль числа а обозначается символом . Тогда |−6|=6; |6|=6.

Приводятся примеры.

,

Отрабатывается навык правильного чтения модуля и изображения чисел на координатной прямой, модуль которых задан. Учащиеся учатся правильно читать модуль числа: "модуль числа -6 равен 6", иногда вместо модуля говорят "абсолютная величина".

|5| = 5
Читается так: модулем числа 5 является 5.

|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.

|0| = 0
Читается так: модулем нуля является ноль.

 Прочитай равенство, используя слово «модуль» и «расстояние» и определи является ли это высказывание истинным?

1) =3;              2)=4;                3) =5;                 4) -=-7.

Образец: Модуль числа 5 равен 5, так как точка с координатой 5 удалена от начала отсчета на расстояние 5 единичных отрезков.

Открыть учебное пособие "Математика 6" (или раздать приложение 1) прочитать теорию к теме, сравнить свои составленные определения с текстом, оценить правильность рассуждений, при необходимости откорректироать информацию. Приложение 1

Работа в парах. Взаимное обучение. Создать пары из представителей разных групп. Для закрепления материала и оценки усвоения теоретического материала предложить задания, аналогичные заданиям Приложения 2 из учебного пособия "Математика 6".

Приложение 2.

Задание 1.

a) Назовите координаты точек, отмеченных на координатной прямой.

b) Какие из данных точек имеют противоположные координаты?

c) Среди данных чисел укажите пары противоположных чисел:

Задание 2. Отметьте координатной прямой точки, модуль которых равен 2, 6, 0. Сколько точек отмечено в каждом случае? Сделай записи.

Задание 3. Найдите модули чисел и запиши значение модулей. Расположи данные числа в порядке убывания модулей, сопоставь им соответствующие буквы, и ты узнаешь название самой северной точки одного из материков. На каком материке находится эта точка?

+42;        0;      -96;         +8;            +1;             -45;          -0,02;         -100

Ю             Н       Е            С                 К                 Л                И               Ч

Проверить ответы по ключам. Сравнить, проверить правильность ответов, провести анализ ошибок.

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями. Учащиеся обсуждают свои действия, сверяют ответы, решив задание самостоятельно.

Приложение 3.

1.Вычисли:

а) +;                   г);              

б) ;                   д) +;                           

в) ;                 е) .

2. Сравни модули чисел:                      

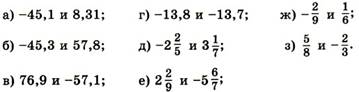
3. Известно, что . Чему равен ? Сделай вывод.

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить ответы по ключам. Сравнить, проверить правильность ответов, провести анализ ошибок.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия. Учащиеся пишут свои мнения и сдают учителю.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена самопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение чертить координатную прямую, правильно выбирать единичный отрезок и отмечать точки с учетом расположения в зависимости от координат, находить правильно модули, сравнивать числа, предварительно найдя модули. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Интернет ресурсы: http://www.yaklass.ru; https://school-assistant.ru