3. Повтор5 класса. Уравнения. Методические указания к уроку.Вариант 2

Методические указания к уроку

тема "Повторение курса математики 5 класса. Уравнение."

Цели обучения

5.2.2.1 решать уравнения на основе правил нахождения неизвестных компонентов арифметических действий;

5.2.2.2 использовать приёмы проверки правильности решения уравнений.

Критерии оценивания

Учащийся:

· правильно называет компоненты арифметических действий;

· знает, что такое уравнение: находить корень уравнения, делает проверку правильности решения;

при решении текстовых задач правильно составляет математическую модель задачи и по нему уравнение.

Теоретический материал.

Из истории

В Древнем Египте и Вавилоне до нашей эры люди умели решать уравнения и задачи, составляя уравнения. Диофант Александрийский,  греческий математик, по сведениям историков, начал использовать буквы при решении таких примеров, которые мы сейчас называем уравнениями.

Первый учебник по решению уравнений написал арабский математик  Мухаммед ибн Муса Хорезми.

Уравнение – это равенство, содержащее букву, значение которой надо найти.

Корень уравнения – это значение буквы, при котором из уравнения получается верное числовое равенство.

Решить уравнение – значит найти все его корни или убедиться, что корней нет.

Уравнения, содержащие более одного действия, называют составными.

Когда нужно назвать буквы в выражениях, то надо помнить:

1) в математике используют латинский алфавит;

2) буквы  мужского рода, а названия остальных латинских букв среднего;

3) при чтении математических выражений названия букв не склоняют.

Ход урока.

Организационный момент:

·                    концентрация внимания учащихся;

·                     совместно определить тему и цели урока/ЦО в процессе повторения темы "Уравнения" и устных упражнений;

·                    определить «зону ближайшего развития» учащихся, ожидания к концу урока.

Повторение материала с целью актуализации знаний.  

В начале урока обобщите и закрепите знания по решению уравнений, полученных ранее в начальной школе. Учебный материал выстраивается в такой последовательности, чтобы учащиеся могли осознать теоретические основы проводимых обобщений.

Для успешной работы всех учащихся активными методами вспомните виды уравнений и все компоненты арифметических действий.

Вопросы к классу:

Как найти неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое, делитель?

  или  ;

  или  ;

  или  ;

  или  .

Желательно, чтобы ученик при ответе приводил пример к правилу и решение примера.

Устный опрос:

1. Какое равенство называют уравнением?

2. Что значит решить уравнение?

3. Что называют корнем уравнения?

4. Сколько корней имеет уравнение? (приведите примеры).

5. Всегда ли уравнение имеет корень?

6. Как сделать проверку правильности решения уравнения?

Предложить ученикам устные упражнения. Приложение 1.

Задание можно организовать по рядам, по группам. Каждой группе предложить 1 столбец и предложить соревнование: Кто быстрее? Решите уравнения на скорость.

Приложение 1

Реши уравнения:

a) ;

b) ;

c)

d) ;

e) ;

f) ;

g) ;

h) ;

i)

j) ;

k) ;

l) ;

m) ;

n) ;

o) .

Индивидуальная работа. Решение уравнений, используя свойства вычитания.

Деятельность учащихся направлена формирование знаний и развитие навыков, относящихся к целям урока,  используя свойства вычитания суммы из числа или вычитания числа из суммы. Приложение 2

1) Реши уравнения, используя свойства

вычитания суммы из числа:   

или вычитания числа из суммы:

a)                  b) ;                   

c)                 d) .

Решение: b) (x + 63) - 17 = 76, используем свойство (a+b)-c=a+(b–c):

x + (63 - 17) = 76;

x + 46 = 76;

x  = 76 - 46;

x = 30.

Ответ: 30.

с) 143-(45+y)=37;

(143 - 45) - y =37;.

98 - y =37;

y = 98 - 37;

y= 61

Ответ: 61.

d) (x+81)-13=101;

x+(81-13)=101;

x+68=101;

x=33

Ответ:33

Коллективная работа. Решение текстовых задач с помощью уравнения.

Вначале деятельности начинаем с примера с геометрическим рисунком. По рисунку составить и решить уравнение, если известен периметр треугольника, а стороны даны буквенными выражениями.

Задача. По рисунку составь и реши уравнение, если известно, что периметр треугольника равен 62 см.

Решение: x+2x+20=62

3x=62-20

3x=42  x= 14

Ответ: 14 см - 1 сторона, 2∙14=28 см - 2 сторона.

Совместно с учащимися составить алгоритм (схему) решения текстовой задачи с помощью уравнения.

При решении задачи, проведи анализ условия, результаты оформи в виде таблицы, схемы, рисунка или краткой записи.

1.    Обозначь неизвестную величину.

2.    Составь буквенное и числовое выражения по условию задачи.

3.    Составь уравнение.

4.    Реши уравнение.

5.    Ответь на вопрос задачи.

Разобрать образец:

Задача. Сумма двух чисел равна 76, а разность их 12. Найди эти числа.

Решение: 1) Пусть  - первое число,  - второе число.

2) Составим буквенное и числовое выражения по условию задачи. Сумма их:  , что составляет 76.

3) Составим уравнение: .

4) Решим уравнение: .

.

5) Ответим на вопрос задачи:

32 - 1 число,

 - 2 число.

Проверка: ;    

Ответ: 1 число - 32, 2 число - 44.

Заготовьте иллюстрации или, при наличии компьютеров, презентацию, чтобы визуально закрепить алгоритм (схему) решения текстовой задачи с помощью уравнения.

Для закрепления решить самостоятельно в парах задачи из Приложения 3.

Приложения 4

Решение текстовой задачи с помощью уравнения

При решении задачи, проведи анализ условия, результаты оформи в виде таблицы, схемы, рисунка или краткой записи.

1.                  Обозначение неизвестной величины.

2.                  Составление буквенного и числового выражений по условию задачи.

3.                  Составление уравнения.

4.                  Решение уравнения.

5.                  Ответ на вопрос задачи.

Реши задачи:

Уровень А

1.                  Представь число 432 в виде суммы двух последовательных нечетных чисел.

Решение: Представь число 432 в виде суммы двух  последовательных нечетных чисел.

х - 1 число, последовательное нечетное - следующее х+1 - второе число.

х-1+х+1= 432;                       2х=432;                      х=216;             х-1=215; х+1=217.

Ответ: 215, 217.

2.                  У Санжара вдвое больше марок, чем у Ануара, а у Мухтара - на 15 марок больше, чем у Санжара. Сколько марок у каждого, если всего у них 115 марок?

Решение:1) У Ануара х марок,

у Санжара - 2∙х марок,

у Мухтара - (2х+15) марок.

Всего:х+2х+2х+15, что составляет 115 марок.

Составим уравнение:х+2х+2х+15=115;               

Решим уравнение:5х+15=115.        5х=115-15;                 5х=100;          х=20.

Ответим на вопрос задачи: 20 марок у Ануара,

20∙2=40(марок) у Санжара,

40+15=55(марок) у Мухтара.

Ответ: 20 марок, 40 марок, 55 марок.

Уровень В

3.                  Кусок полотна в 124 м надо разрезать на 2 части так, чтобы длина одной части была на 12 м больше другой. По сколько метров полотна будет в каждой части?

Решение:

х метров полотна в меньшем куске

х+12 метров в большем куске

х+х+12 метров всего полотна

х+х+12=124

2х+12=124

2х=124-12

2х=112

х=56

56 м в меньшем куске; 56+12=68 метров

Ответ. 56 м и 68 м.

4.                  За конфеты заплатили в 3 раза или на 600 тенге больше, чем за печенье. Сколько заплатили за печенье.

Решение: х тенге заплатили за печенье;

3х тенге заплатили за конфеты;

На 3х-х тенге конфеты дороже печенья;

т. к. за конфеты заплатили на 600 тенге больше, то 3х-х=600;

2х=600;                      х=300.

300 тенге заплатили за печенье

Ответ: 300 тенге.

Уровень С

5.                  В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног.

Решение: Пусть в хозяйстве х овец;

19-х кур;

т. к у овцы 4 ноги, значит 4х – число ног у овцы;

у кур 2 ноги, значит 2(19-х) число ног у кур.

4х+2(19-х) всего ног у овец и кур, значит 4х+2(19-х)=46.

4х+38-2х=46;

4х-2х+38=46;

2х+38=46;

2х=8;

х=4.

4 овец и 19-4=15 кур

Ответ. 4 овцы, 15 кур.

6)Угадай корни уравнения:

a) 15∙a = 15:a.

Ответ: 1.

b) z+z = z∙z.

Ответ: 2.

c) y∙10 = y:10

Ответ: 0

Групповая работа. Деление на группы произвольное. Закрепление понимания алгоритма решения составных уравнений.

Можно группы сделать разноуровневые. Работая в группах, разобрать данный алгоритм и образец решения. Каждый член группы решает не менее 2 уравнений из первого задания. 2 задание решают коллективно.

Алгоритм

1.  Определи порядок действий.

2. Выдели последнее.

3. Рассмотри выражение, находящееся справа и слева от последнего действия и определи вид простейшего уравнения, один из компонентов которого выражение, содержащее переменную х. Обозначь его за Х.

4. Реши новое уравнение.

5. Корень уравнения не найден? Решай, начиная вновь с пункта 1.

Пример решения уравнения: 20 : (33 - 4x) + 47 = 51

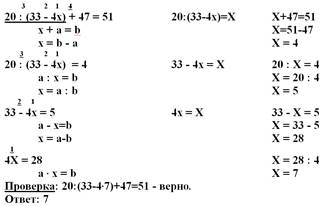
Решить уравнения из Приложения 4.

1)

2)Угадай корни уравнений:

a) ;

b) ;

c) ;

d) .

Задания даны для более глубокого понимания понятия "корень уравнения".

a) х∙х = 85 - 60                       х∙х = 25          x = 5. Проверка: 5 ∙ 5 + 60 = 85.

Ответ: 5.

b) (х∙х-3) ∙9=117 

х∙х - 3 = 117 : 9;         х∙х - 3 = 13;    х∙х = 16; х = 4. Проверка: (4∙4 - 3) ∙ 9 = 117

Ответ: 4.

c)

 х∙х∙х + 38 = 5 ∙ 13;                х∙х∙х + 38 = 65;          х∙х∙х = 65 - 38;           х∙х∙х = 27; х = 3

Проверка: (3 ∙ 3 ∙ 3 + 38) : 13 = 5.

Ответ: 3.

d) (149-х∙х∙х) ∙7=168

149-х∙х∙х = 24;           х∙х∙х = 149 - 24;         х∙х∙х = 125;    х = 5.

Ответ: 5.

Попросите учащихся сделать вывод о значении переменных.

Учитель проходит по рядам, слушает, при необходимости корректирует решения, оказывает помощь слабоуспевающим. По истечению времени попросить учеников озвучить некоторые решения. Обратить внимание на соответствие поставленной цели.

Обменятся решениями между группами для оценки.

Рефлексия. Оценить работу учащихся на каждом этапе урока

Ответить на вопросы:

Что узнал?

Чему научился?

Что осталось непонятным?

Над чем надо поработать?

Дифференциация выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся. Более способным учащимся предлагаются задания более высокого уровня.      Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять формулы.

В ходе коллективной деятельности при решении задач устно оценивается вычислительные навыки учащихся.      Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. При использовании ИКТ применять правила ТБ. Следить за осанкой учащихся.