30. Решение СЛУ. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока " Решение системы линейных уравнений с двумя переменными способом сложения"

Цели обучения:

6.2.2.19

решать системы уравнений способом подстановки и способом сложения;

Критерии оценивания

Учащиеся

знают:

как решать системы уравнений способом подстановки и способом сложения.

умеют

решать системы уравнений способом подстановки и способом сложения.

Теоретический материал

Алгоритм решения системы двух уравнений с двумя переменными x,y
способом подстановки:

1. Выразить одну переменную через другую из одного уравнения системы (более простого).

2. Подставить полученное выражение вместо этой переменной в другое уравнение системы.

3. Решить полученное уравнение и найти одну из переменных.

4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения в уравнение, полученное на первом шаге и найти вторую переменную.

5. Записать ответ в виде пар значений, например, (x;y), которые были найдены соответственно на третьем и четвёртом шаге.

Алгоритм решения системы двух уравнений с двумя переменными x,y
способом сложения:

1. Уравнять модули коэффициентов при одном из неизвестных (если необходимо).

2. Сложить или вычесть уравнения.

3. Решить полученное уравнение с одной переменной, найти неизвестное.

4. Подставить найденное на третьем шаге значение переменной в одно из уравнений исходной системы, найти второе неизвестное.

5. Записать ответ.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Выполнить устно упражнения на повторение:

Приложение 1

1) Если 2а =b + 1, то чему равно а) -2a; б) 4a; в) 6a; г) a; д) 2a+3:

а) -2a = - (b + 1),

б) 4a = 2 · 2a = 2 · (b + 1);

в) 6a = 3 · 2a = 3(b + 1);

г) ;

д) 2a + 3 = (b +1) + 3 = b +4.

2) Заполните пропуски, чтобы запись стала правильным:

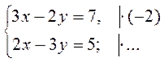
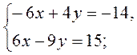
... у = 1; у = ...; 3х - 2 · ...= 7; 3х = ...; х = ...

Ответ. (...; ...).

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. На этом уроке вспомним способ подстановки, способ сложения.

Алгоритм решения систем линейных уравнений с двумя переменными способом подстановки можно несколько трансформировать, а именно: выразить не переменную, а ее линейную комбинацию (то есть, выражать не х, а 2х и т.д.). Лучше всего это показать, как и на предыдущих уроках, на примере решения конкретной системы.

 Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями. Выбор способа за учащимися, если не оговорен в тексте задания.

Приложение 2

1. Решите систему уравнений способом подстановки, учитывая кратность коэффициентов:

а)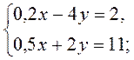                       б) 

2. Решите систему уравнений 2 способами:

а) способом подстановки;

б) способом сложения.

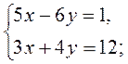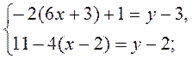1)            2)                    3)  

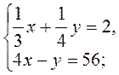
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы учащимся:

1. Какие способы решения систем двух уравнений с двумя переменными вам известны?

2. Какие преимущества у каждого способа?

3. Зависит ли решение системы от выбора способа?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.                  "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.                  "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.                  Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.                  Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.                  Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.                  http://www.yaklass.ru

2.                  https://school-assistant.ru

3.