
Методические рекомендации к уроку
Тема урока " Решение системы линейных уравнений с двумя переменными способом сложения"
Цели обучения:
6.2.2.19
решать системы уравнений способом подстановки и способом сложения;
Критерии оценивания
Учащиеся
знают:
как решать системы уравнений способом сложения.
умеют
решать системы уравнений способом сложения.
Ход урока
Организационный момент. Актуализация опорных знаний.
Проверить домашнее задание.
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".
Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 3. Каждый выполняет самостоятельно.
Вариант 1
1.
Какая из пар чисел является решением линейного уравнения ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2.
Для какого уравнения пара чисел ![]() является
решением?
является
решением?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3.
Решите систему уравнений 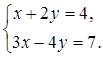
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 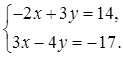
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 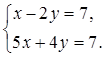
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 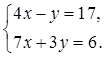
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7.
На каком из рисунков изображено графическое решение системы линейных уравнений 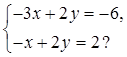
|
1) |
2) |
3) |
4) |
|||
|
|
|
|
|
|
|
|
8.
Найдите координаты точки пересечения графиков уравнений ![]() и
и ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9.
Сколько точек пересечения имеют графики уравнений ![]() и
и
![]() ?
?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
10.
Сколько решений имеет система уравнений 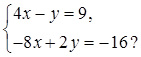
1) 1 2) 2 3) бесчисленное количество 4) ни одного
«Системы линейных уравнений»
Вариант 2
1.
Какая из пар чисел является решением линейного уравнения ![]() ?
?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
2. Для
какого уравнения пара чисел ![]() является
решением?
является
решением?
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
3.
Решите систему уравнений 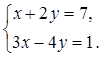
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
4.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 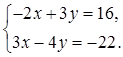
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
5.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 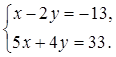
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
6.
Пусть ![]() - решение системы линейных
уравнений
- решение системы линейных
уравнений 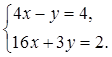
Найдите ![]() . 1)
. 1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
7.
На каком из рисунков изображено графическое решение системы линейных уравнений 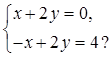
|
1) |
2) |
3) |
4) |
|||
|
|
|
|
|
|
|
|
8.
Найдите координаты точки пересечения графиков уравнений ![]() и
и ![]() .
.
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
9.
Сколько точек пересечения имеют графики уравнений ![]() и
и
![]() ?
?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
10.
Сколько решений имеет система уравнений 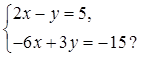
1) 1 2) 2 3) бесчисленное количество 4) ни одного
Ответы:
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
4 |
2 |
2 |
1 |
3 |
2 |
4 |
3 |
4 |
|
2 |
4 |
1 |
3 |
3 |
4 |
2 |
1 |
2 |
4 |
3 |
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.
Работа с классом. Вспомнить и обобщить основные знания и навыки по решению систем двух уравнений с двумя переменными x,y способом подстановки и способом сложения.
Приложение 2
1) ![]()
Решение: I способ подстановки.
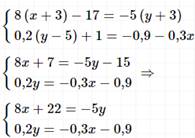
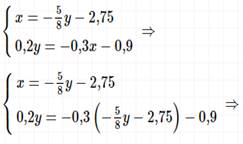
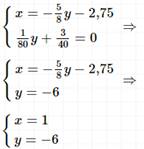
II способ сложения.

Ответ: (1; -6).
2) 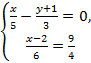
Решение:
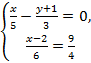 первое уравнение умножим на 15, второе на
12.
первое уравнение умножим на 15, второе на
12.
I способ подстановки.
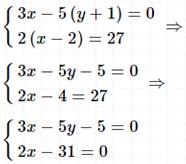
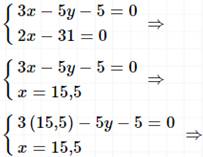
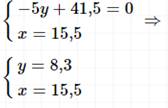
Т.к. во втором уравнении одна переменная, то способом сложения не решаем.
Ответ: (15,5; 8,3).
3) 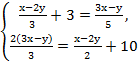
Решение:
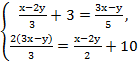 первое уравнение умножим на 15, второе на
6.
первое уравнение умножим на 15, второе на
6.
I способ подстановки.
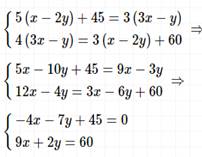
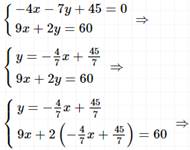
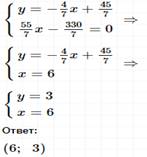
II способ сложения.
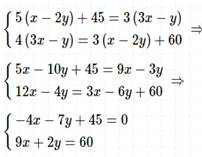
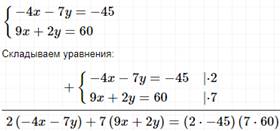
 Ответ: (6; 3).
Ответ: (6; 3).
4) При каких значениях ![]() система
уравнений
система
уравнений ![]() не имеет решений? (а=-1,5).
не имеет решений? (а=-1,5).
Беседа. Рефлексия.
Вопросы учащимся:
1. Какие способы решения систем двух уравнений с двумя переменными вам известны?
2. Какие преимущества у каждого способа?
3. Зависит ли решение системы от выбора способа?
В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.
На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.
Литература:
"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;
"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.
1. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192
2. Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.
3. Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.
Интернет ресурсы:
1. http://www.yaklass.ru
2. https://school-assistant.ru
3.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.