47 Умножение Методические рекомендации к уроку В 2

Методические рекомендации к уроку

Тема урока "Умножение рациональных чисел"

Цели обучения:

6.1.2.15 выполнять умножение рациональных чисел.

Критерии оценивания

Учащийся:

знает:

правила выполнения умножения рациональных чисел:

·         умножение чисел одного знака;

·         умножение чисел разных знаков.

умеет:

выполнять умножение рациональных чисел

Теоретический материал:

Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак «-».

Чтобы перемножить два отрицательных числа, надо перемножить их модули.

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
0 × a = 0
a × 0 = 0
a × 1 = a
Примеры:
0 × (- 3) = 0
0,4 × 1 = 0,4
Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).
При умножении на (- 1) число меняется на противоположное.
В буквенном выражении это свойство можно записать:
a × (- 1) = (- 1) × a = - a
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание:

С помощью заданий Приложения 1 проверить умения учащихся быстро умножать и правильно определять знак произведения:

Приложение 1

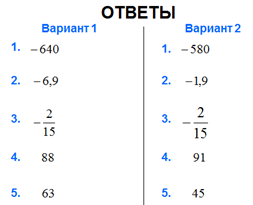
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа с классом. Сделать вывод правила знаков для умножения когда более двух множителей.

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Минус на минус даёт плюс,

Плюс на минус даёт минус.

1) Определите знак произведения:
а) -2 ∙ (-3) ∙ (-9) ∙ (-1,3) ∙ 14 ∙ (-2,7) ∙ (-2,9);

б)4 ∙ (-11) ∙ (-12) ∙ (-13) ∙ (-15) ∙ (-17) ∙ 80 ∙ 90.

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве - отрицательным.

Пример.

(- 6) × (- 3) × (- 4) × (- 2) ×12 × (- 1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 × 3 × 4 × 2 × 12 × 1 = 1728

Конечный результат умножения исходных чисел будет:

(- 6) × (- 3) × (- 4) × (- 2) × 12 × (- 1) = - 1728

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

0 × a = 0                     a × 0 = 0

a × 1 = a         

Примеры:
0 × (- 3) = 0                0,4 × 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).

При умножении на (- 1) число меняется на противоположное.

В буквенном выражении это свойство можно записать: a × (- 1) = (- 1) × a = - a.

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Для закрепления, при наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями.

Приложение 2

Задание 1) Определить знак произведения и сравнить с нулем:

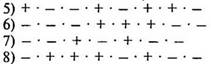
Задание 2) Выполните умножение и сделайте вывод:

Задание 3) Запишите в виде произведения сумму:

Задание 4) Найдите значение выражения:

Задание 5) Догадайтесь, чему равен корень уравнения, и выполните проверку:

а) -8 • х = 72;              б) -4 • х = -40;           в) 6 • у = -54;             г) -6 • у = 66.

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок.

Каждая группа демонстрирует свой результат выполнения задания..

Старший группы оценивает вклад каждого, выставляя отметку.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить задания. Каждый выполняет самостоятельно.

Приложение 3

Выполнить умножение дробей

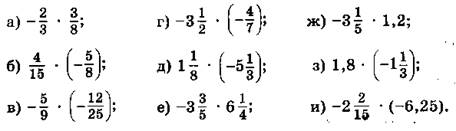
Ответы с решениями:

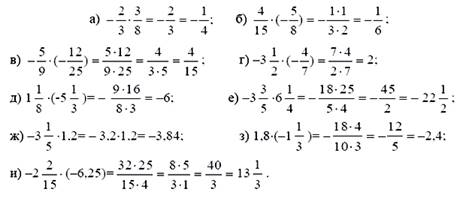
После окончания выполнения, попросить обменяться тетрадями и проверить у товарища результат. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать примеры в которых обнаружились ошибки.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания на нахождение   произведения, опираясь на понятие увеличения или уменьшения величин.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Математика 6 класс Виленкин Н.Я.

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В. 

Интернет ресурсы:

http://www.yaklass.ru

https://school-assistant.ru