5.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: Линейное неравенство с одной переменной. Решение линейных неравенств с одной переменной.

Критерии оценивания:

6.2.2.10 решать линейные неравенства видов  или ;

6.2.2.11 приводить неравенства с помощью алгебраических преобразований к неравенству вида ,

6.2.2.12 изображать решения неравенств на координатной прямой;

6.2.2.13 записывать решения неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства;

Организационный момент.

Актуализация опорных знаний «Это мы знаем».

Для повторения пройденного материала предложите учащимся работу в парах:

Вариант 1

1. Найдите пересечение и объединение промежутков (-5; 1] и [-2; 3), используя координатную прямую.

2. Перечислите элементы пересечения трех множеств А, В и С, если А — множество натуральных двузначных чисел, В — множество чисел, кратных 4, С - множество чисел, кратных 7.

Вариант 2

1. Найдите пересечение и объединение промежутков [-6; 2) и (-3; 1].

2. Перечислите элементы пересечения трех множеств А, В и С, если A — множество натуральных двузначных чисел, В — множество чисел, кратных 5, С — множество чисел, кратных 9.

Учащиеся обмениваются решениями и проводят самооценивание и взаимооценивание.

Попросите учащихся вспомнить определение линейного уравнения с одной переменной и его корней. Проведите аналогию с линейными неравенствами. Предложите учащимся дать определение линейному неравенству и его решению. Сформулируйте проблему: «Как решить неравенство ?».

Обсудите с учащимися свойства числовых неравенств.

Предложите учащимся сделать вывод: Что является решением неравенства с одной переменной?

Линейные неравенства с одной переменной

Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

 Совместно с учащимися составьте алгоритм решения линейных неравенств с одной переменной.

Предложите учащимся индивидуальную работу на соответствие. Учащимся необходимо соединить стрелками неравенство и его решение.

Учащиеся обмениваются решениями и проводят самооценивание и взаимооценивание

Проверка усвоения знаний (самостоятельная работа) + взаимопроверка

Данная работа индивидуальная, по вариантам их 6, по числу членов группы, каждому учащемуся предоставляется право выбрать уровень сложности, сообразно своим ощущениям и возможностям. Взаимопроверка формирует ответственность за принятое решение.

Ученики  оценивают друг друга по критериям оценивания. Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся

Проверка усвоения знаний (самостоятельная работа) + взаимопроверка

Данная работа индивидуальная. Взаимопроверка формирует ответственность за принятое решение.

Решение:

Дескриптор:

- знает алгоритм решения простейшего линейного неравенства;

-изображает решения неравенств на координатной прямой;

- записывает решения неравенств в виде числового промежутка;

Групповая работа. Объедините учащихся в однородные группы по 4 - 6 учеников, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику. Предложите ученикам выбрать уровень сложности задания по закреплению теоретического материала на более высоком уровне. После решение  задачи на доске,  группы меняются задачами и оценивают по дескриптору и записывают пожелания. Ученики  оценивают друг друга по критериям оценивания.

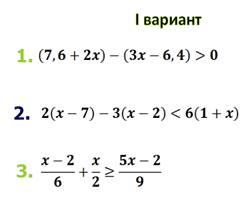
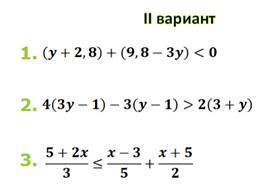
Ответы:

Дескриптор:

- знает алгоритм решения простейшего линейного неравенства;

-изображает решения неравенств на координатной прямой;

- записывает решения неравенств в виде числового промежутка;

Подведение итогов урока. Рефлексия.

•         Что нового узнали на уроке?

•         – Какую цель мы ставили в начале урока?

•         – Проанализируйте свою работу на уроке.

•         - В чем было затруднение?

Домашнее задание: №988 стр.226

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.