6. Методические рекомендации к проведению урока. Вариант 1

Методические рекомендации к проведению урока

Цель обучения:

6.2.2.2 знать определение линейного уравнения с одной переменной, равносильных уравнений;

6.2.2.3 решать линейные уравнения с одной переменной;

Критерии оценивания:

-знает определение линейного уравнения

 -знает алгоритм решения простейшего линейного уравнения

- определяет порядок выполнения действий по приведению заданного уравнения к простейшему линейному;

- верно выполняют вычисления;

Организационный момент. Актуализация знаний.

Ознакомьте учащихся с целями урока и ожидаемыми результатами. Предложите учащимся «Мозговой штурм» для закрепление пройденного материала. Проведите устное формативное оценивание. Учащиеся поднимают руки, отвечают на вопросы.

1. Какие из чисел 3; –2; 2 являются корнями следующих уравнений:

а) 3х = –6;                              г) 4х – 4 = х + 5;

б) 3х + 2 = 10 – х;                 д) 10х = 5(2х + 3);

в) х + 3 = 6;                            е) 10 + х = 13?

2. Являются ли уравнения равносильными? Если да, то сформулируйте, по какому свойству уравнений.

а) 3х + 4 = 2                  и       3х = –2;

б) –3х + 12 + 2х = 4      и       2х + 12 = 3х + 4;

в) 3х + 15 = 0                и       3х = 15;

г) 0,5х = 0,08                и       50х = 8;

д) 120х = –10                и       12х = 1;

е) x = 11                                 и         3х = 44.

Проведите устное формативное оценивание, за каждый правильный ответ – фишку или смайлик.

Предложите учащимся работу в парах, разделите учащихся по парам в зависимости от уровня способностей на базовый, средний и продвинутый. Предложите учащимся выполнить задания в зависимости от уровня сложности. На этом этапе у учащихся развивается уважение друг к другу и академическая честность.Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся. Учащиеся проводят самооценивание своих решении, затем проводят проверку по готовым ответам. Учитель наблюдает за работой учащихся, в случае необходимости оказывая им поддержку.

Ответы:

Дескриптор:

-          верно раскрывает скобки

-          верно собирает подобные слагаемые, содержащие неизвестные, в одной части уравнения, а остальные члены в другой

-          верно приводит подобные слагаемые

-          верно делит обе части уравнения на коэффициент при неизвестном;

Для закрепления темы «Линейные уравнения с одной переменной» предложите учащимся Игру «Палитра уравнений»

 Цель: формирование умений и навыков в решении уравнений, проверка и коррекция знаний учащихся по изученной теме, развитие познавательной компетентности учащихся.

Ценности: формировать чувство ответственности, уверенность учеников в своих силах, развивать умение принять решение.

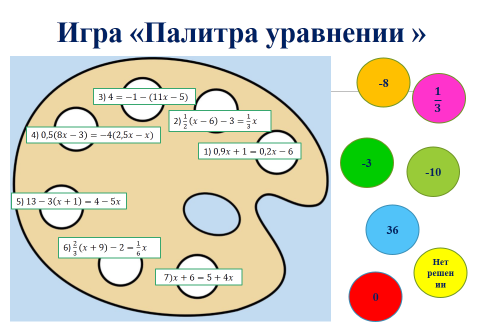
Содержание игры. Учитель раздает ученикам макет палитры. На местах красок записаны уравнения, в центре прикреплены разноцветные кружочки с ответами. Решив уравнение, ученик находит кружочек с правильным ответом, и с помощью двухстороннего скотча прикрепляет его у уравнения. Таким образом, образуется палитра.

Выводы: игра позволяет учителю позаботиться о том, чтобы на уроке математики каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности; играя в «палитру уравнений» ученики совершенствуют умения и навыки в решении уравнений.

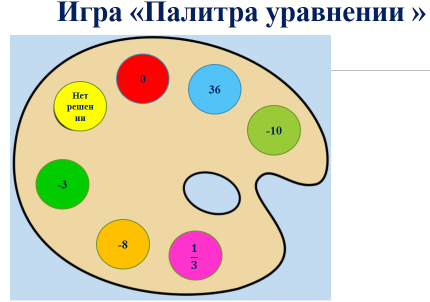
Учащиеся по готовым ответам на презентации выполняют самооценивание, опираясь на критерий оценивания.

Например:

·         Если все верно выполнено, «отлично»,

·         Если ответы правильные, но трудности с обоснованием «хорошо»,

·     Если верно выполнено только 70 работы, то       «нужна практика»

Если верно выполнено меньше 70 работы, то       «нужна помощь».

- знает определение линейного уравнения

 -знает алгоритм решения простейшего линейного уравнения

- определяет порядок выполнения действий по приведению заданного уравнения к простейшему линейному;

- верно выполняют вычисления

Подводим  итоги  урока. 

Учитель возвращает учащихся к целям обучения, критериям успеха.

-какова цель урока?

-достигли ли мы цели?

- какие заданий вы решили?

- Почему вы выполняете эти задания?

В конце урока учащиеся проводят рефлексию:

- что узнал, чему научился

- что осталось непонятным

- над чем необходимо работать

Домашнее задание.

№836 стр. 191

Ресурсы:

1.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.      Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

3.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

4.       Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.