Методические рекомендации к уроку

Тема урока "Решение задач на нахождение средней скорости движения."

Цели обучения:

6.5.1.5

решать задачи на нахождение средней скорости движения;

Критерии оценивания

Учащиеся

 знают:

·         как найти среднюю скорость движения;

·         как решать задачи на нахождение средней скорости движения;.

умеют

·         определять среднюю скорость движения.

Теоретический материал

Средняя скорость вычисляется по формуле

                                    где S – путь пройденный телом

                                    t – время, за которое этот путь пройден.

Если путь состоит из нескольких участков, то следует вычислить всю длину пути и все время движения.

Например, если путь состоит из двух участков протяженностью S₁ и S₂, скорости на которых были равны соответственно V₁ и V₂,  то:

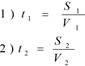
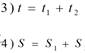
Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Индивидуальная работа. Для повторения и предварительной подготовки усвоения нового материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

1) Найдите время, зная

а) путь S= 168 км, скорость v = 84 км/ч.

б) путь S= 213 км, скорость v = 71 км/ч.

в) путь S= 296 км, скорость v = 74 км/ч.

г) путь S= 189 км, скорость v = 63 км/ч.

2) Найдите расстояние, зная

а) время t= 5 ч, скорость v= 58 км/ч.

б) время t= 7 ч, скорость v = 82 км/ч.

в) время t = 13 ч, скорость v = 91 км/ч.

г) время t = 15 ч, скорость v = 49 км/ч.

3) Найдите скорость, зная

а) путь S = 95 км, время t = 19 ч.

б) путь S = 110 км,  время t = 2 ч.

в) путь S = 200 км,  время t = 4 ч.

г) путь S = 366 км,  время t = 6 ч.

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Работа с классом. Ввод в тему урока, используя основные знания и навыки по решению задач на движение.

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

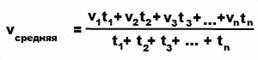
На примерах посмотрим, как находить среднюю скорость.

Приложение 2

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

Решение:

Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.

Находим все время движения: 2+3=5 часов.

Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

Ответ: 5,8 км/ч.

2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.

Решение:

Переведем минуты в часы: 30 минут = 0,5 часа.

Найдем весь пройденный автомобилем путь:

2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.

Находим все время движения:

2 + 1,5 + 0,5 = 4 часа.

Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:

273:4 = 68,25 км/ч.

Ответ: 68,25 км/ч.

3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

Решение:

Найдем весь путь велосипедиста:

3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения:

3 + 1 + 2 = 6 часов.

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

54:6=9 км/ч.

Ответ: 9 км/ч.

Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 3

1) Общая длина трассы в гонке формулы 1 составила 480 км. Какой была средняя скорость болида, если вся гонка длилась 2 часа?

2) Пилот формулы 1 завершил гонку за три часа, проехав 90 кругов. Его средняя скорость составила 180 км/ч. Какова длина одного круга?

3) Длина бобслейной трассы 2310 метров. Спортсмены совершили спуск за 70 секунд. Найдите скорость бобслейных саней в м/с.

4) Пешеход шёл по дороге 2 часа со скоростью 6км/ч, по болоту 3 часа со скоростью 2км/ч, и по полю 1час со скоростью 6км/ч. Найдите среднюю скоростью пешехода.

Решение:

1)      6 · 2 = 12 (км) – расстояние, которое пешеход прошёл по дороге

2)      2 · 3 = 6 (км) – расстояние, которое пешеход прошёл по  болоту

3)      6 · 1 = 6 (км) – расстояние, которое пешеход прошёл по полю

4)      2 + 3 + 1 = 6 (ч) – общее время

5)      12 + 6 + 6 = 24 (км) – весь путь

6)      24 : 6 = 4 (км/ч) – средняя скорость

Ответ: 4 км/ч

5) Первый час автомобиль ехал со скоростью 115 км/ч, следующие три часа - со скоростью 45 км/ч, а затем два часа - со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути

Решение:

115∙1=115 (км) проехал за 1 ч

45∙3=135 (км) проехал за 3 ч

40∙2=80 (км) проехал за 2 ч

115+135+80=330 (км) проехал всего

1+3+2=6 (ч) ехал всего

330:6=55 (км/ч)

Ответ: средняя скорость 55 км/ч.

6) Первые 120 км пути авто ехал со скоростью 75км/ч, следующие 90 км - со скоростью 60 км/ч, а затем 190 км- со скоростью 100км/ч.Найдите среднюю скорость

Решение:

120+ 90 + 190 = 410 (км) общий путь

 (ч) общее время

410/5 = 82 (км/час) средняя скорость

Ответ: средняя скорость 82 км/ч.

Сравните задачи 1-3 с задачами 4-6. Сделайте вывод правил для каждой группы задач.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы   учащимся:

– Что называют средней скоростью?

– Что значит найти «среднюю скорость»?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru