7. Методические рекомендации к проведению урока. Вариант 1

Методические рекомендации к проведению урока

Цель обучения:

6.2.2.2 знать определение линейного уравнения с одной переменной, равносильных уравнений;

6.2.2.3 решать линейные уравнения с одной переменной;

Критерии оценивания:

-знает определение линейного уравнения

 -знает алгоритм решения простейшего линейного уравнения

- определяет порядок выполнения действий по приведению заданного уравнения к простейшему линейному;

- верно выполняют вычисления;

Организационный момент. Актуализация знаний.

Ознакомьте учащихся с целями урока и ожидаемыми результатами.

Предложите учащимся Конкурс «Веселая рыбалка». Объединить учащихся в однородные группы по 4 - 6 учеников, согласно выбранному уровню. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику.

Три ученика с каждой группы «ловят» рыбку. На рыбке написано одно из уравнений, которое надо решить, записать на доске решение, болельщики решают все уравнения. Рыбаки получают балл за то, что поймали (при помощи удочки с магнитом) и удержали рыбку и два балла за правильно решенное уравнение. Группа может помочь своим игрокам. Проведите устное формативное оценивание, за каждый правильный ответ – фишку или смайлик.

Ответы:

Предложите учащимся игру «Найди фамилию ученого».  Найдите фамилию немецкого математика, решив примеры. Ответ и соответствующую букву запишите в таблицу и вы прочитаете фамилию ученого. (Учитывается скорость команды.) Если группа правильно решила примеры и правильно заполнила таблицу, то получили фамилию немецкого ученого МЕБИУС. Проведите оценивание по готовым ответам.

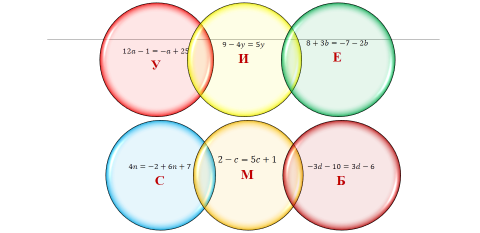
Ответы:

      Предложите учащимся информацию об ученом:  Август Фердинанд Мебиус (1790 – 1868 г) немецкий математик и астроном. Считается одним из создателей современной геометрии. Установил существование односторонних поверхностей. Лист Мебиуса – простейшая односторонняя поверхность, которая получается при склеивании полоски бумаги прямоугольной формы.

У вас есть полоска бумаги прямоугольной формы, перекрутите ее, склейте, вы получили Лист Мебиуса.

Август Мебиус обнаружил, что на перекрученном кольце линия от карандаша прошла по обеим сторонам, хотя его карандаш не отрывался от бумаги. Позже математики открыли еще целый ряд «односторонних поверхностей». Но эта, первая, положившая начало целому направлению в геометрии.

Дескриптор:

-          верно раскрывает скобки

-          верно собирает подобные слагаемые, содержащие неизвестные, в одной части уравнения, а остальные члены в другой

-          верно приводит подобные слагаемые

-          верно делит обе части уравнения на коэффициент при неизвестном;

Предложите учащимся Групповую работу. Решение практических задач. Для закрепления и оценки уровня умения решать линейные уравнения с одной переменной, предложите ученикам решить предложенные уравнения. Объедините учащихся в однородные группы по 4 - 6 учеников «Считалкины» (Уровень А), «Мешалкины» (Уровень В), «Смекалкины» (Уровень С), согласно выбранному уровню. Ученики в группе выполняют задания индивидуально, поделив задачи между собой, но имеют возможность обсудить непонятные вопросы в группе.

Считалкины (Уровень А)

1. Какие из чисел являются корнями уравнения:

 а) 3х - 4=2;   [x=2]

б) х+3= -х+4? [x=]

2. Решите уравнение:

а)5х-3=17; [x=4]         

б)9-6х=3х-6; [x=]        

 в)4(х-2)=2х+6; [x=7]    

3. Составьте уравнение равносильное данному: 4х-3=5.[3x+3=9]

4. Сумма двух чисел 114, причем первое число на 42 больше второго. Найдите эти числа.[78;36]

Решалкины (Уровень В)

1.      Решите уравнение .

2.      Решите уравнение .

3.      Решите уравнение .

4.      Решите уравнение .

5.      Решите уравнение .

Смекалкины (Уровень С)

1.      Решите уравнение .

2.      Решите уравнение .

3.      Решите уравнение .

4.      Решите уравнение .

5.      Решите уравнение .

Учащиеся по готовым ответам на презентации выполняют самооценивание, опираясь на критерий оценивания.

Например:

·         Если все верно выполнено, «отлично»,

·         Если ответы правильные, но трудности с обоснованием «хорошо»,

·     Если верно выполнено только 70 работы, то       «нужна практика»

Если верно выполнено меньше 70 работы, то       «нужна помощь».

- знает определение линейного уравнения

 -знает алгоритм решения простейшего линейного уравнения

- определяет порядок выполнения действий по приведению заданного уравнения к простейшему линейному;

- верно выполняют вычисления

Подводим  итоги  урока. 

Учитель возвращает учащихся к целям обучения, критериям успеха.

-какова цель урока?

-достигли ли мы цели?

- какие заданий вы решили?

- Почему вы выполняете эти задания?

В конце урока учащиеся проводят рефлексию:

- что узнал, чему научился

- что осталось непонятным

- над чем необходимо работать

Домашнее задание.

№836 стр. 193

Ресурсы:

1.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.      Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

3.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

4.       Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.