7Факториал. Дидактикалық материал

Есептер

1.    «орамал» сөзінің әріптерінен бір дауысты және бір дауыссыз дыбыстан құралатындай неше жұп құрастыруға болады?

Шешуі: дауысты: а, о – 3-еу;   дауыссыз: р, м, л – 3-еу. Олай болса 3 • 3 = 9

Жауабы: 9 тәсілмен.

2.    8 ұл мен 6 қыз баладан неше би жұбын құруға болады?

Шешуі: 6 • 8 = 48

Жауабы: 48 жұп.

3.    Асханада біріншінің 4 түрі, екіншінің 7 түрі бар. Әртүрлі екі тағамнан тұратын түскі асқа тапсырыс берудің неше нұсқасы болады?

     Шешуі: 4 • 7 = 28

Жауабы: 28 нұсқа.

4.    1, 4 және 7 цифрларын қолданып, цифрлары қайталанатын неше әртүрлі үштаңбалы сан құрастыруға болады?

Шешуі:  1 цифрын таңдаудың 3 тәсілі, 2 цифрын таңдаудың 3 тәсілі, 3 цифрын таңдаудың 3 тәсілі бар. Олай болса, 3 • 3 = 9

     Жауабы: 9 сан.

5.    3 және 5 цифрларын қолданып, цифрлары қайталанатын неше әртүрлі үштаңбалы сан құрастыруға болады?

Шешуі: 1 цифрын таңдаудың 2 тәсілі, 2 цифрын таңдаудың 2 тәсілі, 3 цифрын таңдаудың 2 тәсілі бар. Олай болса,  2 • 2 • 2 = 8

Жауабы: 8 сан.

6.    Отбасында 6 адам және олардың ас үй бөлмесінде 6 орындық бар. Отбасы мүшелері әр кеш сайын кешкі тағамда орындықтарға әр түрлі әдіспен отыруға келісті. Олар осыны неше күн бойы жасай алады?

Шешуі: Ыңғайлы болу үшін отбасы мүшелерін «атап» аламыз: атасы, әжесі, әкесі, анасы, қызы, ұлы. Олай болса, әжесінің орындық таңдауының 6 тәсілі, атасының – 5 тәсілі, әкесінің - 4 т–сілі, анасының – 3 тәсілі, қызының – 2 тәсілі және ұлының 1 тәсілі бар. Демек көбейту ережесі бойынша 6×5×4×3×2×1 = 720 (күн).

7.    Әртүрлі 10 кітаптың 3-і анықтамалар. Барлық анықтамалар бірге тұратындай етіп, 10 кітапты сөреге жинаудың неше тәсілі бар?

Шешуі: Анықтамалар бірге тұратын болғандықтан, оларды бір кітап ретінде қарастырамыз. Олай болса, сөреге 10 – 3 + 1 = 8 кітап орналастыру керек. Мұны жүзеге асырудың 8! тәсілі бар.  Сондай – ақ анықтамалардың өзара бірге тұруының 3! тәсілі бар екенін ескереміз. Сонымен  барлық анықтамалар бірге тұратындай етіп, 10 кітапты сөреге жинаудың 8! · 3! = 40 320 · 6 = 241 920 тәсілі бар.

8.      Есепте:

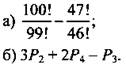
9.      Есепте:

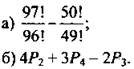
10.              Ықшамда:    a) n!/(n+1)!;                  б) n!/(n-2)!;                 

                                 в) (n+1)!/(n-2)!;             г) n!/(n-k)! , n>k

11.  Ықшамда :        а) 1/(n+1)! – 1/(n+2)!    б) n!/(n+1)! – (n-1)!/n!

                                 в) (n-1)!/n!                      г) n!/(n-3)!.

12.  Ықшамда:        а) 1/k! – 1/(k+1)!             б) (n-2)!/n! – n!/(n+1)!

                                 в) (n-2)!/(n-4)!                 г) (n+1)!/(n-k+1)! , n>k

13.  Теңдеуді шешіңіз:   а) (n+2)!/n! = 72      б) (n+1)!/(n-1)! = 30

14.  Есепте:                     а) (P₅+P₄)/P₃            б) (P₁₀ - P₉)/9P₈               в) P_3k/P_(3k-2) 

15.  Есепте:                     а) (P₆+P₅)/P₄            б) (P₁₂ – P₁₁)/11P₁₀          в) P_(3k+2)/P_(3k+1)