Методические рекомендации к уроку

Тема урока "Линейное неравенство с одной переменной. Решение линейных неравенств с одной переменной"

Цели обучения:

6.2.2.10

решать линейные неравенства видов kx > b, kx ≥ b, kx < b, kx ≤ b

6.2.2.11

приводить неравенства с помощью алгебраических преобразований к неравенству вида

kx > b, kx ≥ b, kx < b, kx ≤ b;

6.2.2.12

изображать решения неравенств на координатной прямой;

6.2.2.13

записывать решения неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства.

Критерии оценивания

Учащиеся

 знают:

□     как решать линейные неравенства видов kx > b, kx ≥ b, kx < b, kx ≤ b

□     как приводить неравенства с помощью алгебраических преобразований к неравенству вида kx > b, kx ≥ b, kx < b, kx ≤ b;

□     как записывать, используя математическую символику, ответы к решениям неравенства;

умеют

□     решать линейные неравенства видов kx > b, kx ≥ b, kx < b, kx ≤ b

□     изображать решения неравенств на координатной прямой;

□     использовать обозначения для записи числовых промежутков в ответах;

□     записывать решения неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства;

Теоретический материал

I) Неравенство вида .

В этих случаях неравенство либо не имеет решений, либо его решением является любое число.

Если b — отрицательное число, то решением неравенства  является любое число,

если b — неотрицательное число, то неравенство не имеет решений.

II) Неравенство вида

В этих случаях неравенство либо не имеет решений, либо его решением является любое число.

Если  — положительное число, то решением неравенства  является любое число,

если  — неположительное число, то неравенство не имеет решений.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание. Устно определить ответы.

Приложение 1

Выбери правильный ответ в виде числового промежутка.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 2

В а р и а н т  1

1. Решите неравенство:

а)  ;                            б)   .

2. При каких значениях  двучлен  принимает положительные значения?

В а р и а н т  2

1. Решите неравенство:

а)  ;                            б)   .

2. При каких значениях  двучлен  принимает положительные значения?

О т в е т:

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Работа с классом: Обратить особое внимание учащихся при разборе заданий на неравенства вида  и вида

1. Создание   проблемной   ситуации.

На  предыдущих  уроках  мы решали неравенства вида ах > b (ax < b), где а ≠ 0. Алгоритм решения был прост: мы преобразовывали неравенства к такому виду, а затем делили обе части неравенства на коэффициент а (с учетом знака) и получали числовой промежуток в качестве решения. Пробуем применить этот алгоритм к следующему упражнению:

2(х + 8) – 5х < 4 – 3х;

2х + 16 – 5х < 4 – 3х;

2х – 5х + 3х < –16 + 4;

0 · х < –12.

Наш алгоритм «не работает» – на нуль делить нельзя. Замечаем, что неравенство будет иметь решение, если при подстановке какого-то числа вместо х мы получим верное неравенство. Но в данном случае при любом значении х неравенство обращается в числовое 0 < –12, которое является неверным, значит, исходное неравенство не имеет решений.

II. Решить самостоятельно упражнения:

Приложение 3

Решить неравенство

1) 0х < 136

x – любое число.

Ответ: .

2)  2(х+8)-5х<4-3х

2х+16-5х<4-3х

2х-5х+3х<4-16

0∙х<-12

Неравенство не имеет решений.

Ответ: Решения нет

3) 5х+6 >  5(х-3)  

5х-5х>-15-6

0∙х>-21

Так как 0 больше любого отрицательного числа, то решением неравенства будет любое число.

Ответ: х –любое число либо можно записать: х Î(–∞; +∞)

4) 5(х + 11) – 9х < 65 – 4х;

5х + 55 – 9х < 65 – 4х;

5х – 9х + 4х < 65 – 55;

0 · х < 10.

Замечаем, что при любом значении х неравенство обращается в верное числовое неравенство 0 < 10, значит, решением является любое число.

Ответ: х –любое число

III) Делаем общий  вывод: неравенства вида 0 · х > b (0 · x < b), а значит,  и  неравенства,  равносильные  данным,  либо  не  имеют  решений,  либо их решением является любое число (множество решений либо , либо (–∞; +∞)).

I) Неравенство вида .

В этих случаях неравенство либо не имеет решений, либо его решением является любое число.

Если b — отрицательное число, то решением неравенства  является любое число,

если b — неотрицательное число, то неравенство не имеет решений.

II) Неравенство вида

В этих случаях неравенство либо не имеет решений, либо его решением является любое число.

Если  — положительное число, то решением неравенства  является любое число,

если  — неположительное число, то неравенство не имеет решений.

Приложение 4

1) Решить неравенство .

2) Решите неравенство .

3) Решить неравенство:

Ответы:

1) Решить неравенство .

Решение:  

Слагаемые с  соберём в левой части, а числа – в правой и приведём подобные слагаемые:

.

Получим: 0∙y£-12

Неравенствоне имеет решений, так как при любом значении у обращается в неверное числовое неравенство.

Ответ: Решений нет.

2) Решите неравенство .

Решение:

Раскроем скобки. Слагаемые с  соберём в левой части, а числа – в правой и приведём подобные слагаемые:

.

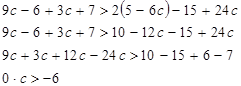Неравенствоверно при любом значении с. Значит, решением неравенства является вся числовая прямая.

Ответ:  - любое число..

Ответ ещё можно записать как:  или .

3) Решить неравенство:

Решение: , так как НОК (3;2) =6, умножим обе части неравенства на 6.

Раскроем скобки. Слагаемые с  соберём в левой части, а числа – в правой и приведём подобные слагаемые:

Обе части неравенства делим на число, стоящее перед иксом. Так как -25 — отрицательное число, знак неравенства при этом изменяется на противоположный:

x>-0,04

Ответ: (-0,04;+).

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 5

1) Решить неравенство:  .

2) Решить неравенство:  −(6x+7)<−6x.

3) Решить неравенство: 

а) −2(5x+7)<−10x;

б) 31(2х + 1) – 12х > 50х;

в) .

4) Найти наибольшее целое число, удовлетворяющее неравенству: 1,6 – (3 – 2у) < 5;

5) Найти натуральные решения неравенства (2 – 2п) – (5п – 27) > 0

Решения:

1) Решить неравенство:  .

Решение.

Неравенство не имеет решений, т.к. при любом  его левая часть равна нулю и не может быть больше 3.

Ответ: нет решений или

2) Решить неравенство:  −(6x+7)<−6x.

Решение. ;                      ;      

 ;          .

Неравенство верно при любом значении , т.к. при любом  его левая часть равна нулю и меньше 7.

Ответ:  — любое число.

3) Решить неравенство:  а) −2(5x+7)<−10x.

Решение. ;                  ;           

 ;   .

Неравенство верно при любом значении , т.к. при любом  его левая часть равна нулю и меньше 14.

Ответ:  — любое число.

Решение. б) 31(2х + 1) – 12х > 50х;

62х + 31 – 12х > 50х;

62х – 12х – 50х > –31;

0 · х > –31;

при любом значении х имеем верное неравенство 0 > –31, значит, х – любое число.

в)  ; умножим на 3 обе части.

3х + 12 – х < 2х;

3х – х – 2х < –12;

0 · х < –12;

при любом значении х имеем неверное неравенство 0 < –12, значит, неравенство не имеет решений.

Ответ: а) х – любое число; б) нет решений.

4) Найти наибольшее целое число, удовлетворяющее неравенству: 1,6 – (3 – 2у) < 5;

Р е ш е н и е

1,6 – (3 – 2у) < 5;

1,6 – 3 + 2у < 5;

Наибольшее целое число, удовлетворяющее неравенству, равно 3.

Ответ: 3.

5) Найти натуральные решения неравенства (2 – 2п) – (5п – 27) > 0

Р е ш е н и е

(2 – 2п) – (5п – 27) > 0;

2 – 2п – 5п + 27 > 0;

Данному неравенству удовлетворяют натуральные числа 1, 2, 3, 4.

Ответ:1; 2; 3; 4.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.

Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru