
Методические указания к уроку
тема " Пропорция. Основное свойство пропорции"
Цели обучения
6.1.2.3 знать определение пропорции;
6.1.2.4 распознавать и составлять пропорции;
6.5.2.2 читать и записывать пропорции;
6.1.2.5 знать и применять основное свойство пропорции.
I. Организационный момент:
Для концентрации внимания учащихся провести опрос.
задание 1. Закончить фразу
1. Отношение двух чисел – это …
2. Отношение 1:5 показывает, что …
3. Отношение 3:2 показывает, что …
4. Если отношение двух чисел больше единицы, то это означает, что …
5. Если первое число в три раза больше второго, то они относятся как …
6. Если первое число в полтора раза меньше второго, то они относятся как …
7. Если первое число относится ко второму как 4:7, то второе число относится к первому как…
Совместно определить тему и цели урока/ЦО в процессе повторения темы "Отношения" и устных упражнений; определить «зону ближайшего развития» учащихся, ожидания к концу урока.
Вычислите отношения и расшифруйте тему урока:
|
1) |
0,6 : 0,2 |
|
И |
|
2) |
|
|
О |
|
3) |
1,8 : 3 |
|
Я |
|
4) |
2 : 4 |
|
Р |
|
5) |
|
|
Ц |
|
6) |
|
|
П |
Какие из отношений равны?
|
П |
Р |
О |
П |
О |
Р |
Ц |
И |
Я |
|
0,2 |
0,5 |
2 |
0,2 |
2 |
0,5 |
0,8 |
3 |
0,6 |
В качестве проблемного задания предложить ученикам задание 1.
Найдите значения частных
3,6:1,2= 3
7:5 = 1,4
9:3 = 3
8,4:6 = 1,4
Какие из отношений равны? Запишите равенства отношений
![]() 3,6:1,2=9:3; 7:5 = 8,4:6
3,6:1,2=9:3; 7:5 = 8,4:6
пропорции
Изучение нового материала. Учащимся предлагается сформулировать понятие пропорции и проверить себя. На примерах разбирается понятие пропорции, устанавливается верность пропорции, основываясь на основное свойство пропорции. Учащиеся учатся читать и записывать пропорции. Работа происходит с проверкой на слайде с последующим комментарием учащихся.
Пропорция — это равенство двух отношений.
1
: 3 = 2 : 6 ![]()
Так как пропорция - это равенство, в случае если это равенство содержит переменную, значение которой надо найти, то оно является уравнением. Пропорции используются для решения некоторых задач.
В частности, пропорции облегчают решение задач на проценты.
Запишем пропорцию в общем виде: a : b = c : d,
В зависимости от местоположения a, d – крайние члены;b, c - средние члены.

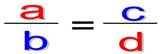
Читают так:
a так относится к b как c относится к d или отношение a к b равно отношению c к b
Закрепить упражнениями следующего содержания:
Прочитайте пропорцию, 1) назовите ее крайние и средние члены: 7 ׃ 8 = 14 ׃ 16;
проверьте 2) верна ли пропорция?
Ввести свойства пропорции.
Основное свойство пропорции. Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.
Задание: Как, используя основное свойство пропорции, проверить будет ли данное отношение пропорцией?
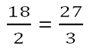 Чтобы правильно применять правило,
предложить учащимся запомнить правило (икса) «X».
Чтобы правильно применять правило,
предложить учащимся запомнить правило (икса) «X».
Рассмотрим его на примере пропорции.
Убедимся, что пропорция составлена верно. 18: 2= 9; 27:3=9.
 Теперь
запишем пропорцию и нарисуем карандашом
Теперь
запишем пропорцию и нарисуем карандашом
поверх знака равенства (икс) «X».
Нарисовав икс, гораздо легче составить нужное произведение (выполнить основное свойство пропорции).
 ;
; ![]() ;
; ![]()
Если в верной пропорции поменять местами средние члены или крайние члены, то получившиеся новые пропорции тоже верны.
7 3 : 6 = 5 : 10; 3 : 5 = 6 : 10; 10 : 5 = 6 : 3; 10 : 6 = 5 : 3.
Например: Даны числа 4, 5, 12, 15. Составлена верная пропорция 5 : 15 = 4 : 12 (1).
5 : 4 = 15 : 12 - поменяли средние члены (2).
12 : 15 = 4 : 5 – поменяли крайние члены (3).
12 : 4 = 15 : 5 поменяли крайние члены в пропорции 2 (4).
Задание: составить три новые пропорции из данной 2 : 4 = 5 : 10
Решение: 10 : 4 = 5 : 2; 2 : 5 = 4 : 10; 10 : 5 = 4 : 2.
Перед переходом к закреплению данной темы, дайте учащимся историческую справку о пропорциях. Пропорция (от латинского proportio ) – определенное соотношение частей между собой, соразмерность.
Учение о пропорциях возникло в глубокой древности , примерно в VI в. до н. э. ,в эпоху Пифагора. Однако латинское слово «пропорция» для обозначения равенства двух отношений стали использовать лишь начиная с I в. н.э.
Евклид или Эвклид (др.-греч. Εὐκλείδης, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по основам математики «Начала» (Στοιχεῖα букв.элементы). Считается “отцом геометрии’’. В его книге “Hачала” подробно изложена теория отношений и пропорций. Там же доказано основное свойство пропорции.
«Божественная пропорция». С пропорциями связаны представления о красоте, порядке и гармонии в природе, искусстве, архитектуре, скульптуре и музыке. Соблюдение определенных соотношений между размерами отдельных частей тела, предмета непременное условие красоты. У математиков средневековья и древности существовал термин “божественная пропорция” или “золотое сечение”. Золотым сечением называется деление отрезка, при котором длина всего отрезка относится к длине большей части, как длина большей части относится к длине меньшей части. Это отношение нельзя точно выразить обыкновенной или десятичной дробью, а приблизительно оно равно числу:
![]()

«Золотое сечение» в природе



Рассматривая расположение трех подряд идущих пар листьев на общем стебле растения, можно заметить, что между третьей и первой парой вторая находится в месте «золотого сечения». При таком расположении листьев, как утверждают биологи, достигается максимальное восприятие солнечных лучей.
Теоретические упражнения.
Предварительная проверка усвоения теории.
Теоретические упражнения. Для оценки уровня достижения целей обучения урока, предложить ученикам решить задачи из Приложения Математический диктант
Подбор вопросов зависит от уровня класса. Дифференцированный подход как к количеству, сложности вопросов, так и оцениванию осуществляет учитель.
Математический диктант.
|
1 |
Закончите предложение: «Равенство двух отношений называют … |
1 |
Запишите предложение выражением: «7 так относится к 21, как 1 к 3» |
|
2 |
Запишите пропорцию 7:21=1:3. Подчеркните ее средние члены. |
2 |
Запишите пропорцию 3:4=9:12. Подчеркните ее средние члены. |
|
3 |
Запишите
предложение выражением: |
3 |
Закончите предложение: «Равенство двух отношений называют … |
|
4 |
Является ли данное равенство пропорцией 3:5=6:10. |
4 |
Является ли данное равенство пропорцией 24:8=6:3. |
Проверь себя!
|
1 |
Пропорцией |
1 |
7:21=1:3 |
|
2 |
7:21=1:3 |
2 |
3:4=9:12 |
|
3 |
3:4=9:12 |
3 |
Пропорцией |
|
4 |
Да 3:5=6:10 0,6=0,6. |
4 |
Нет 2:8=6: 3= |
Первичное закрепление нового материала. Уровень усвоения каждой цели обучения проверяется через решения задач. Для закрепления материала и оценки усвоения теоретического материала предложить задания по готовым рисункам.
Используя рисунки, составить пропорции и решить:
а) 2 задачи решить совместно с классом,
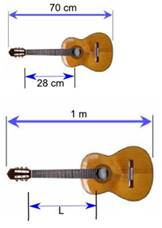
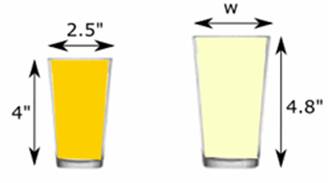
б) Для следующих трех рисунков составить пропорции в парах и решить Сколько пропорций смогли составить?
1)

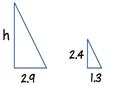 2)
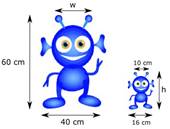
2) 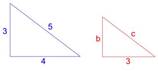 3)
3)
Слушать работу учеников, при необходимости попросить учащихся озвучить ответы.
В конце урока учащиеся проводят рефлексию:
 - С какой темой мы
познакомились на уроке?
- С какой темой мы
познакомились на уроке?
- Что такое пропорция?
- Как называются числа х и у в пропорции х : а = в : у
- Как называются числа m и n в пропорции a : m=n : b?
- Приведите свои примеры верных пропорций.
- Какие задания вызвали у вас трудность?
- Что больше всего понравилось на уроке?
Оставьте стикер со своим именем на радуге успеха.
Домашнее задание: уровень А: № , уровень Б: №
На уроке предусмотрена дифференциация в виде работы в однородных группах (одного уровня обучаемости). Ученики самостоятельно выбирают уровень сложности заданий. Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять свои знания. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. Следить за осанкой учащихся.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.