Методические рекомендации к уроку

Тема урока "Линейное уравнение с одной переменной, содержащее переменную под знаком модуля"

Цели обучения:

6.2.2.4

решать уравнения вида , где a и b – рациональные числа;

Критерии оценивания

Учащийся:

знает:

как решать уравнения вида , где a и b – рациональные числа;

умеет:

решать уравнения вида , где a и b – рациональные числа.

Теоретический материал:

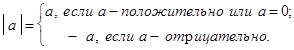
Геометрически  |a| означает расстояние на координатной прямой от начала отсчета до точки, изображающей число a.

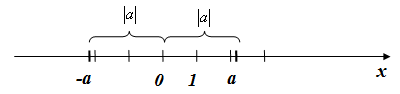
Если , то на координатной прямой существуют две точки a и -a, равноудаленные от нуля, модули которых равны.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Провести устный опрос.

Дать определение модуля числа.

Как найти значение модуля.

Геометрический смысл модуля?

Как находить расстояние между точками на координатной прямой?

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями с целью проверки остаточных знаний.

Приложение 1

Разделите уравнения на группы по количеству корней, обоснуйте свой выбор, решив уравнение.

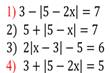
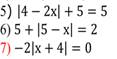
Вывод запишите в виде схемы

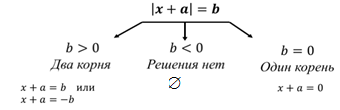
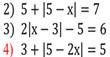
Выбрав из каждого столбца уравнение, обосновать решение и прокомментировать.

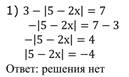
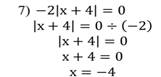                      Ответ: -4.

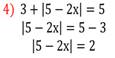
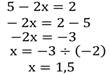
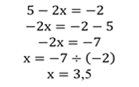
Ответ: 1,5; 3,5.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Работа с классом. В режиме диалога решить более сложные уравнения.

Приложение 2

1) Решить уравнения, предварительно упростив:

а) 3|5x|+ 4|5x| = 35

Решение: а) 3|5x| + 4|5x| = 35 <=> (3 + 4)|5x| = 35 <=> 7 |5x| = 35 <=> |5x| = 35/7 <=> |5x| = 5
Из последнего уравнения мы получаем 5x = 5 или 5x = - 5. x = 1 или x = -1

б)

Решение: б) |2x|/3 + 3|2x|/2 = 1/2 . Умножим на 6, чтобы получить целые коэффициенты.

2|2x| + 9|2x| = 3 <=> 11|2x| = 3 равно <=> |2x| =
Поэтому 2x =  или 2x = - , откуда x =   или x = -

в) 3,7|x| – 2,2|x| = 22,5

Решение: в) 3,7|x| – 2,2|x| = 22,5 <=> (3,7 - 2,2)|x| = 22,5 <=> 1,5|x| = 22,5 <=>
|x| = 22,5:1,5 <=> |x| = 15, откуда x = 15 или x = - 15

2) Используя определение модуля решить уравнения:

а)  | | х – 1 | – 1 | = 2.

Решение.

1. Чем данное уравнение отличается от предыдущих? (Двойным модулем.)

2. Сколько сначала составим уравнений? (Два.)

3. Какие могут получиться уравнения? (| х – 1 | – 2 = 2, | х – 1 | = 3;

 | х – 1 | – 1 = –2, | х – 1 | = –1.)

4. Что можно сказать об уравнении | х – 1 | = –1? (Нет решений, так как модуль (расстояние) – неотрицательное число.)

| | х – 1 | – 1 | = 2

1) | х – 1 | – 1 = 2,                  2)  | х – 1 | – 1 = – 2

| х – 1 | = 3;                             | х – 1 | = – 1; нет решения

х – 1 = 3,        х – 1 = – 3, 

х = 4;              х = – 2.

Проверка:

| | 4 – 1 | – 1 = 2, | | 3 | – 1| = 2, | 3 – 1 | = 2, | 2 | = 2, 2 = 2 – верно;

| | - 2 – 1 | – 1| = 2, | | –3 | – 1 | = 2, | 3 – 1 | = 2, | 2 | = 2, 2 = 2 – верно.

Ответ: – 2, 4.

б) |3 - 2 |x - 5|| -4 =1

Решение.

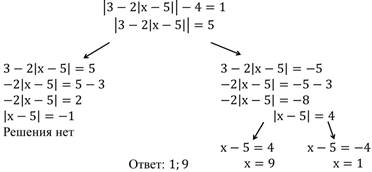
При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся три варианта заданий. Каждый выполняет самостоятельно.

Приложение 3

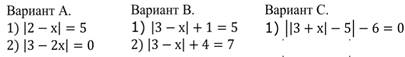
Ответ:

После окончания выполнения, попросить обменяться тетрадями. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать один из вариантов.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru