Алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Свойства логарифмов - Показательная и логарифмическая функции

Цель: продолжить рассмотрение свойств логарифмов.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (тест).

Вариант 1

1. Найдите область определения функции 

Ответы: 

2. Найдите наименьшее значение функции 

Ответы: a) log₄11; б) 1; в) -2; г) 0,5.

3. Решите уравнение 

Ответы: а) -2; б) 1; в) -23; г) -4.

Вариант 2

1. Найдите область определения функции 

Ответы: 

2. Найдите наибольшее значение функции 

Ответы: 

3. Решите уравнение 

Ответы: а) -16; б) -1; в) 0,5; г) -6.

III. Изучение нового материала

Разумеется, после введения нового понятия логарифма и новой операции логарифмирования необходимо изучить их свойства. Это необходимо для более эффективного решения самых разнообразных задач. Рассмотрим ряд теорем.

Теорема 1. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел, т. е. 

Докажем это утверждение. Обратите внимание на доказательство, т. к. подобная схема используется и при рассмотрении других свойств логарифмов и основана на свойствах степеней.

Обозначим:  Надо доказать, что выполняется х = у + z. Так как log_a(bc) = х, то bc = а^х. Из равенства log_ab = у следует, что b = a^y; из равенства log_aс = z получаем с = a^z. Перемножая соотношения b = a^y и с = a^z, имеем  Сравним это равенство с равенством bc = a^x и получим a^y+z = а^x, откуда x = у + z, т. е. 

Пример 1

Вычислим: 

Используя доказанную теорему, получаем:

Теорема 2. Логарифм частного двух положительных чисел равен разности логарифмов этих чисел, т. е. 

Теорема доказывается полностью аналогично предыдущей.

Пример 2

Решим уравнение: 

а) Используя теорему 2, получаем  Из определения логарифма имеем 3 - 2х = 2¹ = 2. Решая это линейное уравнение, находим х = 1/2.

б) Применяя теоремы 1 и 2, получаем   Тогда имеем 3х – 2 = 5¹ = 5, откуда 3х = 7 и х = 7/3.

Теорема 3. Логарифм степени положительного числа равен произведению показателя степени на логарифм основания степени, т. е. 

Опять аналогично теореме 1 докажем это утверждение. Введем обозначения  и  Надо доказать, что х = rу. Из равенства  имеем: b^r = a^x, а из равенства  получаем: b= a^y. Возведем последнее равенство в степень r, тогда  Сравнивая соотношения  получаем равенство  или х = rу. Теорема доказана.

Пример 3

Известно, что log₅2 = а и log₅3 = b. Выразим log₅72 через величины а и b.

Число 72 разложим на простые множители 72 = 2³ ∙ 3². Используя теоремы 1 и 3, получаем:  

Заметим, что теоремы (и соответствующие формулы) 1-3 требуют внимательного отношения и справедливы только для положительных логарифмируемых чисел.

Пример 4

Запишем формулу 1 в случае отрицательных чисел b и с.

Очевидно, что в данном случае формула 1 напрямую бессмысленна, т. к. логарифм от отрицательно числа не существует. При этом произведении bc > 0 и его можно записать в виде  (по определению и свойству модуля числа). Тогда формула 1 имеет вид:  При этом очевидно, что числа (-b) и (-с) положительные.

Таким образом, если числа b и с одного знака (или положительные, или отрицательные), формулы 1 и 2 имеют вид: 

Аналогично можно показать, что при b или положительном или отрицательном и четном показателе степени (т. е. r = 2n, n ∈ Z) формула 3 имеет вид: 

Наконец, отметим еще одно свойство, вытекающее из монотонности логарифмической функции.

Теорема 4. Равенство  справедливо тогда и только тогда, когда t = s.

Пример 5

Решим уравнение 

Сгруппируем члены уравнения, зависящие от х, в левой части, не зависящие от х - в правой. Используем свойства логарифмов и преобразуем уравнение. Получаем:  или  или  Так как равны логарифмы величин, то равны и сами величины. Получаем рациональное уравнение  тогда 63(2х + 3) = 125(х + 2) или 126х + 189 = 125х + 250, откуда х = 61.

Разумеется, свойства логарифмов можно использовать и в более сложных задачах.

Пример 6

Вычислим значение выражения:

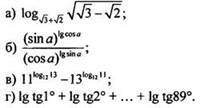
а) Учтем, что  откуда  Теперь легко посчитать данное выражение: 

б) Используем определение логарифма. Тогда  и  Данное выражение имеет вид: 

в) Вновь применим определение логарифма. Так как в данном выражении уже есть логарифмы по основанию 12, то запишем числа в виде:  Теперь вычислим значение данного выражения: 

г) Используем формулу для логарифма произведения чисел, группировку множителей и формулу приведения. Получаем:

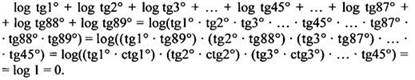
IV. Контрольные вопросы

1. Дайте определение логарифма числа.

2. Перечислите основные свойства логарифмов (фронтальный опрос у доски).

3. Докажите любое свойство логарифмов (по своему выбору).

V. Задание на уроках

§ 43, № 2 (а, б); 4 (в, г); 5 (а); 8 (б); 11 (а); 13 (в); 18 (а, б); 19 (а); 22 (б); 25 (а, б); 28 (а); 29 (в); 30 (а, б); 34 (а); 37 (а, б).

VI. Задание на дом

§ 43, № 2 (в, г); 4(а, б); 5 (б); 8 (а); 11 (б); 13 (г); 18 (в, г); 19 (б); 22 (а); 25 (в, г); 28 (б); 29 (г); 30 (в, г); 34 (б); 37 (в, г).

VII. Подведение итогов уроков