Алгебраический метод решения геометрических задач

Алгебраический метод решения геометрических задач

 

Глава 1. Основные теоретические сведения об алгебраическом методе решения геометрических задач

 

1.1.          Решение геометрических задач на вычисление

Под задачей на вычисление понимают такую ​​задачу, в которой требуется данные о геометрической фигуре привести к установлению числового результата. Задача на вычисление характеризуется требованием установить данные о неизвестном элементе геометрической фигуры с помощью чисто геометрических выкладок с использованием алгебраических зависимостей.

Задача на вычисление с числовыми данными является частным случаем задачи с параметрическими данными, поэтому часто возникает необходимость рассматривать именно их.

Считается сложившимся мнение о том, что в решение геометрической задачи на вычисление с параметрическими данным должно войти исследования области существования геометрической фигуры. Такого взгляда придерживается Л. Н. Фридман, который утверждает, что решение геометрической задачи на вычисление с параметрическими данными сводится к задания функции-формулы, которая показывает, «операции и в каком порядке надо выполнить над значениями параметров, чтобы найти размер искомого элемента. Но для задания какой-либо функции недостаточно назвать закон соответствия, а необходимо еще указать область ее определения» [11].

Функциональный подход к трактовке понятия решения задачи можно сохранить, если рассматривать его как доказательство соответствующей теоремы, составленной по условию данной задачи. Суть этого подхода проиллюстрируем примером.

Задача 1. Длина стороны основания правильной треугольной пирамиды равна а, двугранный угол при основании равна α. Вычислите объем пирамиды.

Будем считать, что нам дана (или она существует) правильная треугольная пирамида со стороной основания а и двугранным углом α при основании. Надо вычислить объем этой пирамиды.

 

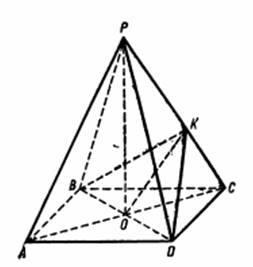
Рисунок 1.

 

Будем исходить из того, что когда дана правильная треугольная пирамида со стороной основания а и двугранным углом α при основании, то высота пирамиды равна , а объем равен.

Суть решения задачи заключается в том, что мы заменяем его доказательством теоремы: если в правильной треугольной пирамиде сторона основания равна а, а двугранный угол при основании равен а, то ее объем равен .

Итак, задача будет решена, если докажем только что сформулированную теорему.

Выражение для объема пирамиды является функцией от параметров а и α, нахождение которой составляет цель решения задачи.

С логической точки зрения решение геометрической задачи на вычисление схематично можно представить следующим образом: Если фигура Ф существует и имеет свойства А, то она также имеет свойства В.

Предположение о существовании геометрической фигуры, заданной условием задачи, нужно обосновать, то есть найти условия, при которых фигура существует. Необходимыми условиями в данной задаче будут: а> 0, 0°<α<90°.

Чтобы убедиться, что они являются достаточными достаточно доказать возможность построения правильной треугольной пирамиды со стороной основания а и двугранным углом α у основания, где а> 0, 0° <α <90 °.

Приступая к решению геометрической задачи на вычисление, каждый раз приходится учитывать особенности конфигурации, описанной в условии задачи. Часто это сложная задача, которая требует высокой культуры вычислений и понимание сути найденных зависимостей.

 

 

1.2.          Решение задач на доказательство

 

Задача на доказательство в геометрии характеризуется требованием обосновать определенное математическое утверждение, сформулированное в ее условии. Решить геометрическую задачу на доказательство означает вывести утверждение задачи из аксиом и ранее доказанных теорем или последствий из них.

Геометрические задачи на доказательство бывают двух видов:

а) такие, при решении которых предполагают, описанные в их условиях геометрические фигуры существуют;

б) такие, в которых факт существования геометрической фигуры, о которой идет речь в задаче, надо доказать.

В первом случае решение задачи сводится к обоснованию вывода, исходя из посылки задачи («дано»). При этом переформулирование условия задачи часто выступает средством поиска решению задачи, поскольку позволяет решить другую, способ решения которой известен или его можно найти сравнительно проще.

Задача. В правильной четырехугольной пирамиде через сторону основания проведена плоскость, перпендикулярная противоположной боковой грани. Сторона основания пирамиды равна а, двугранный угол при основании равен α. Докажите, что площадь сечения равна а² sin³ α, где 45°<<α<90°.

Решение.

Пусть PABCD – изображение правильной пирамиды, о которой идет речь в условии задачи (рис. 2). Построим апофемы РК и РЕ пирамиды. Поскольку  пирамида правильная, то   РКО = РЭО. По условию задачи: РЭО = α, AD = a.

 

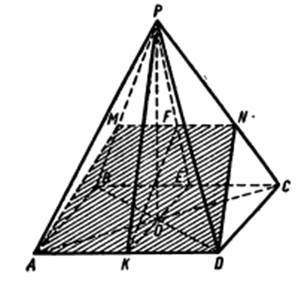
Рисунок 2.

В плоскости треугольника РКЕ проведем KF   РЭ. Построим плоскость, проходящую через прямые AD и KF. Так как AD || ВС, то AD || пл. ВРС, следовательно, AD II MN, где MN - линия пересечения плоскостей ADF и ВРС. Итак, AMND - трапеция. Остается доказать, что AMND – искомое сечение, то есть пл. AMND     пл. РВС.

Действительно, AD    пл. РКЕ, поэтому AD     РК, AD     КЭ, поэтому AD     KF. Но AD || MN, тогда MN   KF. Кроме того, KF    РЕ по построению, следовательно, KF и. пл. ВРС.

Поскольку пл. AMND проходит через прямую KF, то пл. AMND     пл. РВС.

Площадь сечения вычислим по формуле:

Из прямоугольных треугольников KFE и PKO найдем соответственно:

Из прямоугольного треугольника PKF₁

 

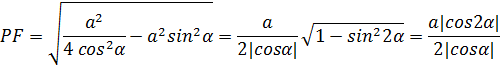
Условия существования сечения AMND найдем из того, что FKE < РКЕ, или 90 ° - α <α, откуда α> 45°. С другой стороны, PKE + РЕК <180°, то есть α + α <180° или a <90°. Итак, 45° <α <90°, поэтому 90° <2а <180°, и cos 2α <0, cos α> 0. Из-за этого

Поскольку MN || ВС, то  PMN    РВС, поэтому

Отсюда

 

Учитывая предыдущие выкладки, получим:

где a>0, 45°<α<90°

 

Как видим, использование условий существования сечения позволило упростить найденное выражение  для вычисления искомой величины.

 

1.3.          Решение задач на построение

 

Под задачей на построение понимают задачу, в которой надо построить геометрическую фигуру заранее обусловленными инструментами, если дана некоторая другая фигура и обозначены определенные соотношения между элементами данной и искомой фигур.

Решить задачу на построение означает свести ее к конечному числу элементарных построений, которые выполняются с помощью чертежных инструментов на основе принятых аксиом конструктивной геометрии.

Решение геометрической задачи на построение обычно осуществляют по схеме, которая состоит из четырех этапов: 1) анализ; 2) построение; 3) доведение; 4) исследования.

С логической точки зрения алгоритм решения задачи на построение не всегда можно реализовать, потому что этап «построение» принципиально возможен, а практическое выполнение построения зависит от выбора величины данных в условии отрезков и углов.

Составляя план решения задачи, следует стремиться к тому, чтобы он основывался только на необходимых условиях, то есть на таких свойствах геометрических фигур, которые вытекают из существования решения. По планам, сложенным только по необходимым условиям, можно найти все решения задачи и указать все случаи их отсутствия (для тех значений параметров, при которых эти условия являются необходимыми). Другой план решения не может дать решений, отличных от найденных по такому плану. Итак, если во время составления плана использованы только необходимые условия существования геометрической фигуры, описанной условию задачи, то исследования задачи можно проводить по плану ее решения.

В процессе исследования задачи по составленному в анализе планом отдельные случаи решения сначала устанавливают, как возможные результаты выполнения определенных пунктов плана. Далее для каждого из этих случаев можно найти условия, которые их определяют. Обычно такие условия выражаются алгебраическими или трансцендентными неровностями (иногда уравнениями), связывающие параметры, характеризующих заданные в задаче величины и взаимное размещение заданных геометрических фигур.

Чтобы решение задачи на построение было полным, надо добиваться, чтобы в области существования искомой геометрической фигуры отдельные случаи, которые рассматривались при анализе и исследовании, охватывали все множество фигур, определенную условием задачи.

Задача. В равнобедренном треугольнике основание равно 12 см., абоковая сторона 10см. Найти высоту, проведенную к боковой стороне?

Решение

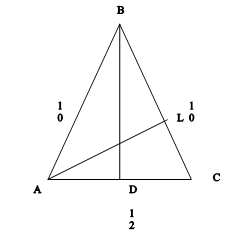
Рисунок 3.

Пусть  . Тогда з ∆ALB имеем, что AL²=AB²-BL².

Аналогично из треугольника ∆ALС имеем, что AL²=AС²-СL².

Отсюда, AB²-BL²=AС²-СL², тоесть 10²-(10-х)²=12²-х².

100-100+20х-х²=144-х², 20х=144, х=7,2, то есть . отсюда

Ответ:  9,6 см

Глава 2. Применение алгебраического метода в решении геометрических задач

 

2.1 Схема решения геометрических задач алгебраическим методом

 

Каждый метод решения задач на построение основывается на зависимостях между геометрическими величинами. Однако в чисто геометрических методах такие зависимости не выражаются  аналитически (исключение составляет отыскания некоторых ГМТ). В алгебраическом методе зависимости между заданными и искомыми величинами записываются в виде уравнений. В связи с этим схема решения конструктивных задач приобретает заметно другое содержание.

Алгебраический метод целью и одновременно результатом анализа видит получение одного или нескольких уравнений, связывающих нужные для построения величины с заданными (известными). На этом анализ заканчивается.

 

Таблица 1.

Суть алгебраического метода в зависимости от типа задач

Задачи	Суть метода
на вычисление	По условию задачи составляется уравнение (система), из которого исчисляется искомая величина.
на доказательство	По условию задачи составляется уравнение (система), решив его убеждаемся в справедливости утверждения задачи.
на построение	а) По условию задачи состоит уравнения; б) выполняется решение задачи; в) исследуются полученные формулы; г) проводится построение искомых величин по полученным формулам.

Таким образом, любая геометрическая задача построена так, что в ней по данным элементам надо найти другие (искомые) элементы геометрической фигуры, находящиеся между собой и данными элементами в определенных соотношениях, или определить размеры отдельных элементов.

В геометрических задачах различных типов - на вычисление, доказательство, построение или исследования термины «найти», «искомые» имеют конкретный смысл, который следует хорошо понимать.

 

2.2 Решение геометрических задач алгебраическим методом

 

Рассмотрим примеры решения задач.

 

Задача 1. Построить треугольник по a; b; .[12]

Решение. Анализ показывает, если провести прямую, параллельную биссектрисе C и продолжить сторону ВС до пересечения с этой прямой в точке D, то образуются равнобедренный треугольник ACD. Пусть AD = x. Поскольку треугольник  и ВDА подобные,  или

Построив отрезок AD, можно построить треугольник CD А (АС = СD), а затем и треугольник АВС.

Задача 2. вершин данного треугольника, как из центров, описать три круга, которые попарно касаются внешне [12].

 

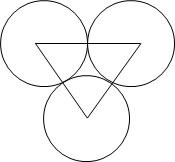
Рисунок 4.

Решение. Пусть А, В, С – вершины данного треугольника; a, b, c – его стороны. тогда

 

Поэтому

 

Итак

 

Построим один из отрезков, например ,  и проведем окружность с центром в точке А радиуса, длина которого равна . Два других круга проводим из центров В и С в соответствии радиусов  и .

Задача 3. Построить треугольник АВС по а; А; ; (Задача Паппа)[6].

Решение. Опишем на стороне ВС дугу сегмента, содержащую угол А и дополним ее в окружность. Продлим биссектрису до пересечения с этим кругом в точке W. Отрезок -заданий (М₁ - середина отрезка BC). Обозначим . Проведем диаметр WD. прямоугольные треугольники і WA - подобные. Пусть

 ; WD=d,

тогда , или .

Найдем x:

 

 

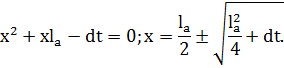
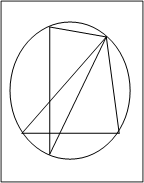
 Рисунок 5.

Из точки W проведем дугу радиуса , получим точку A .

Задача 4. Построить треугольник АВС по R; r; h. [12]

 

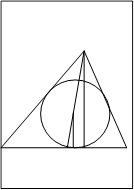
 Рисунок 6.

Решение. Обозначим I центр вписанной треугольника АВС окружности, К₁ - точку касания вписанной окружности со стороной ВС,

- биссектрису угла ВАС. Поскольку (- основание высоты ), то  .

Но

Итак,  или .

 Используем формулу

 

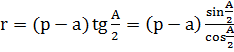
Итак,

Отсюда .

 Итак,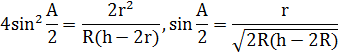

 

Когда найден угол А, нетрудно построить треугольник

 

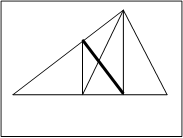
 Рисунок 7.

 

Задача 5. Через точку D, которая принадлежит стороне ВС треугольника АВС, провести прямую, разделяет площадь треугольника пополам [6].

Решение. Пусть DE - искомый отрезок.

Тогда .

Если  М₁ ─ середина отрезка ВС, то .

Итак . Таким образом, чтобы найти точку Е,

 проведем отрезок М₁Е параллельный AD.

Отрезок DE - искомый

 

 

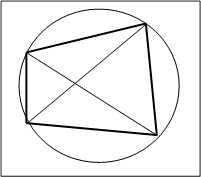
Рисунок 8.

 

Задача 6. По данным сторонам построить четырехугольник, вокруг которого можно описать окружность [12].

Решение.  Пусть АВСD – искомый треугольник, вокруг которого можно описать окружность.

Обозначим АВ = а, ВС = b, DC = c, AD = d, BD = x. Из треугольника BDA по теореме косинусов следует

 

Аналогично, из треугольника DCB имеем

Поскольку , то , то исключив cosA с обеих уравнений, получим

 

Отсюда

 

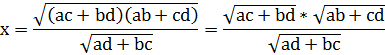
Построив диагональ х, строим сначала треугольник BDA по трем сторонам (a, d и x), а дальше треугольник DCB. Четырехугольник ABCD - искомый

 

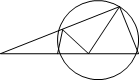
Рисунок 9.

 

Задача 7. В окружность вписан треугольник. На хорде АВ построить точку М так, чтобы

Решение. Пусть точка М - искомая

тогда

Если, , то , откуда находим, что =. Это значит, что круг соприкасается хорды АВ. Итак задача сводится к такой: из С и D провести окружность, касательное к хорде АВ. Обозначим Е точку пересечения прямых DC и АВ, а К - точка соприкосновения. Тогда

 

 

 

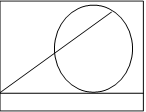
Рисунок 10.

 

Найдем точку К и через точки К, С, D проведем окружность.

 

Задача 8. По гипотенузе с построить такие прямоугольные треугольники, чтобы расстояние МI было: 1) наименьшим; 2) наибольшим, (М - центроид, I - инцентр).

                                             

 

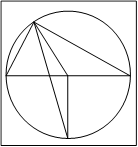
Рисунок 11.

Решение. Очевидно,

   

 По теореме косинусов

 

откуда

причем

поэтому  

или 9  

Отрезок MI достигает наименьшего значения при максимальном r. Но r достигает наибольшего значения при то есть, когда искомый треугольник равнобедренный. В этом случае

 

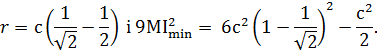
Значит,

 

Отрезок MI достигает наибольшего значения при наименьшем значении r, то есть при r = 0.У этом случае треугольник вырождается.

 

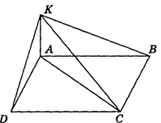Задача. Из вершины A квадрата АВСD проведены перпендикуляр KA к его плоскости. Найдите расстояние CK, если KA равна 6 см, а сторона квадрата - 4√2 см.

 

 

 

 

Рисунок 12.

Решение.

Проведем диагональ АС квадрата АВСD. ΔАСK - прямоугольный, поскольку KA ⊥ АС по определению перпендикулярности прямой и плоскости.

По данной стороной квадрата находим его диагональ:

АС = АD√2 = 4 ∙ √2 ∙ √2 = 8 см.

С ΔАСK по теореме Пифагора получим:

CK =  см.

Ответ: CK = 10 см.

 

Задача.  Из данной точки до плоскости проведено три уровня наклонных длиной 14 см. Расстояние между концами наклонных равны 9 см. Найдите расстояние от данной точки до плоскости.

 

 

 

 

 

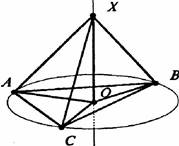Рисунок 13.

Решение.

Пусть ХА = XВ = XС = 14 см, АВ = ВС = АС = 9 см. Проведем перпендикуляр XО к плоскости α. ОА = ОВ = ОС как проекции равных наклонных. Поэтому точка О - центр окружности, проходящей через концы этих наклонных. Найдем радиус окружности, описанной около равностороннего треугольника АВС.

R =  см.

С прямоугольного треугольника XОС по теореме Пифагора получим:

XО = см.

Ответ: XО = 13 см.

 

Задача. Периметр ромба равен 20 см, а сумма его диагоналей - 14 см. Найти площадь ромба.

Решение

 

 

 

 

 

 

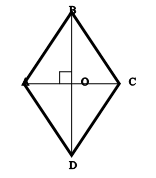
Рисунок 14.

.

Пусть.

Тогда;

.

Так как диагонали ромба взаимно перпендикулярны::

то .

По условию  см, значит см.

Тогда;    ;      , .

Значит см, см (или см, см).

Отсюда, площадь ромба вычисляется см.

Ответ: 24 см.

 

Задача. Площади граней прямоугольного параллелепипеда равны 20 см, 24 см и 30 см. Найдите объем параллелепипеда, в см3.

Решение: Сначала выполним построение, это позволит представить с чем имеем дело. Обозначим стороны параллелепипеда через a, b, c.

 

 

 

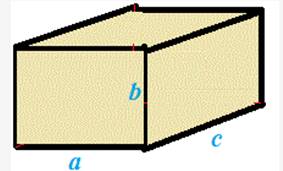
Рисунок 15.

 

Составим уравненя к задаче на основе условия:

1) a×b=20;

2) b×c=24;

3) c×a=30.

Чтобы определить одну из неизвестных умножим первое на третье уравнение и разделим на второе.

В результате получим

a×a=20×30/24=25; a=5.

Из уравнений находим остальные стороны параллелепипеда

с=30/a=30/5=6; b=24/c=24/6=4.

Вычислим объем параллелепипеда

V=4×5×6=120 (см³).

 

Задача. Вычислить катеты прямоугольного треугольника по радиусу r вписанной окружности и гипотенузой с.

Решение. Пусть О - центр, ОК, ОМ, ОР - радиусы вписанной окружности (рис. 16), по свойству отрезков касательных, проведенных из одной точки в окружность, имеем: АР = AM, ВК = ВМ. Обозначим АВ = с, АС = х, ВС = у.

Имеем:

где 

но х+у=с+2r,

 поэтому xy=r(c+2r+c), или xy=2r(c+r)

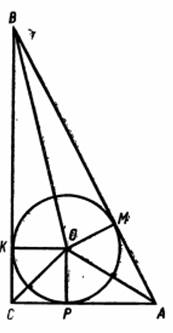
                                                 Рисунок 16.

 

Получили систему уравнений

На основе теоремы Виета х и у - суть корни уравнения:

 

 

Решив его получим:

 

Исследование. Областью существования треугольника АВС является:

0< АС < АВ

Используя это свойство, получим:

Решив систему уравнений, имеем:

Ответ: Катеты равны:

Причем

 

 

Задача. Периметр равнобедренного треугольника равен Р, а его боковая сторона на m больше основания.

Найдите высоту, опущенную на боковую сторону.

Решение. Обозначим AS = ВС = х, BD = у,

где AD  ВС. Тогда по условию задачи х + х + х - m =  Р,

откуда

 Выразив AD из прямоугольных треугольников  ADB и  ADC, получим:

 

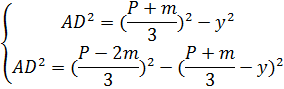
Решив систему уравнений, получим:

 

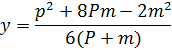
Найдем высоту AD:

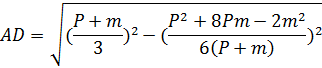
Исследование. Необходимым и достаточным условиям существования равнобедренного треугольника ABC является:

0 < АС < 2ВС

Учитывая предыдущие выкладки, получим:

Решив систему уравнений, получим:

Ответ. Высота треугольника равна:

 

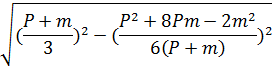
При этом: 

 

Задача. Вычислите объем правильной четырехугольной пирамиды, зная двугранный угол α между боковыми гранями и расстояние d от центра основания до бокового ребра.

Решение. Построим OK  PC, тогда PC  пл. BKD, следовательно, BKD - α.

Но BO = QD, поэтому  OKD - , OK = d.

Объем пирамиды вычислим по формуле:

 

Обозначим , тогда ОК:OD = OK:OC

или

Но ,   поэтому

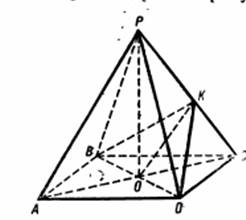
Рисунок 17.

 

Имеем:

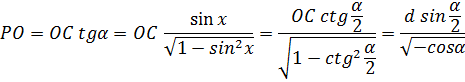
Учитывая предыдущие выкладки, получим:

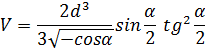
Исследование. По условию задачи найдем:

d > 0, 0° < α < 180°, PO > 0

Эти условия являются необходимыми и достаточными для существования данной пирамиды. Действительно, если d > 0 и 0° < а <180°, существуют равнобедренный треугольник BKD и квадрат ABCD, поэтому существует отрезок ОС> 0. Если РО> 0, СО> 0, существует прямоугольный треугольник РОС, следовательно, существует тетраэдр POCD, а следовательно, и пирамида PABCD.

Из того, что , и учитывая  d > 0, 0° < α < 180°, PO > 0, получим:

d > 0, 90° < α < 180°

Ответ: объем пирамиды  равен

 

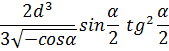
Причем  d > 0, 90° < α < 180°

 

 

Задача. В параллелепипеде длины трех ребер, выходящих из одной вершины, равны а, b, с. Ребра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол α. Найдите объем параллелепипеда.

Решение. Построим А₁К  -пл. АВС. По условию задачи: АВ = a, AD = b, AA₁ = c,  A₁AB =  A₁AD = α.

По теореме косинусов для трехгранного угла:

cos α = cos  А₁АК × cos BAK,

или cos α =cos  А₁АК × cos  DAK,

откуда BAK = cos DAK,

но 0° <  BAK < 90°, 0° < DAK < 90°,

 поэтому  BAK  = DAK — 45°

Найдем:

 

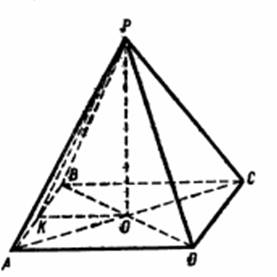
Рисунок 18.

Из прямоугольного треугольника А₁АК:

 

Искомый объем равен: abc

Исследование. В качестве вспомогательной фигуры возьмем тетраэдр А₁АВD. Областью его существования будет:

a > 0, b > 0, c > 0, 2α > 90°, 2α + 90° < 360°

Действительно, если а > 0,  c > 0, 0° < α < 180°, существует  АА₁В, значит, существуют вершины А₁ и В. Аналогично можно доказать существование вершины D.

Если 2α + 90° < 360°, существует трехгранный угол с ребрами, которые являются сторонами треугольников  АА₁В, ABD, AA₁D.

Тогда существует тетраэдр АА₁ВD, значит и параллелепипед АС₁. Значит a > 0, b > 0, c > 0, 45° < α < 135°.

Ответ:  объем параллелепипеда равен abc

Причем a > 0, b > 0, c > 0, 45° < α < 135°.

 

Задача. Одно ребро треугольной пирамиды равна b, каждое из остальных - а. Найдите объем пирамиды.

Решение. Пусть PA = РО = PC  = АВ = АС = а, ВС = b. Построим AD  ВС, РО  пл. ABC, тогда АО  РО. Объем пирамиды вычислим по формуле:

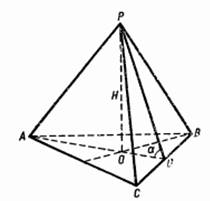
Рисунок 19.

Имеем

Поскольку РА = РВ = PC, то ОА = ОВ = ОС, то есть точка В - центр окружности, описанной около треугольника ABC, тогда:

  

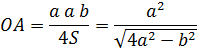
Из прямоугольного треугольника РОА:

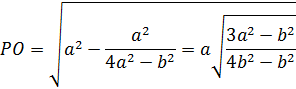
Исходя из предыдущих выражений, получим:

Исследование. В качестве вспомогательной фигуры примем тетраэдр PODC. Необходимыми и достаточными условиями его существования являются:

0 < CD <ОС, РО > 0

Действительно, если 0 < CD < ОС, существует прямоугольный треугольник ODC, а когда ОС > 0, РО > 0, существует прямоугольный треугольник РОС, существует тетраэдр PODC, а, следовательно, и пирамида РАВС.

Учитывая, что a > 0, b > 0, имеем:

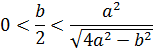
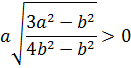
Решив систему неравенств, получим:

Ответ: Объем пирамиды равен

где 

 

Задача. В основании пирамиды лежит прямоугольник. Каждое боковое ребро пирамиды равно l и образует со смежными сторонами основания углы α  и β. Найдите объем пирамиды.

Решение. По условию задачи PC = l,  PCD = a, РСВ = β. Построим ОМ  CD, OKBC, тогда PM , PK  BC.

Найдем

Нo 

 

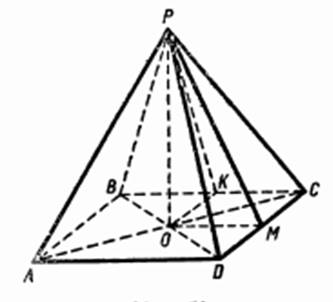
Рисунок 20.

Из прямоугольного треугольника РOС:

Получим:

Исследование. Как вспомогательную фигуру выберем тетраэдр РОКС. Необходимыми и достаточными условиями его существования являются:

0 <  0 К < 0 С < PC.

Действительно, эти условия определяют область существования сиcтемы прямоугольных треугольников ОКС, РОС, РКС, а они - область существования тетраэдра РОКС и, следовательно, пирамиды PABCD.

По условию задачи:

l > 0, 0° < a < 90°, 0° < р < 90°.

Выразим OK > ОС, PC через l, α, β. Поскольку ОК = CM, то получим:

Решив эту систему и учитывая условия, получим:

l > 0, 90 ° < α + β <180°.

 Ответ: объем равен

Задача. В правильной треугольной пирамиде двугранный угол при боковом ребре равен α. Найдите высоту пирамиды, если расстояние от основания высоты к боковому ребру равен d.

Решение. Построим С₁В₁ || СВ, OD РА, тогда PA пл. B₁C₁D, поэтому B₁DC₁ = α, OD = d (по условию задачи).

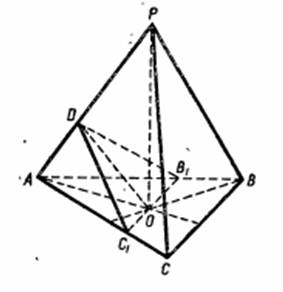
Рисунок 21.

Поскольку

то

но

кроме того

Исходя из даннусловий, получим:

Откуда: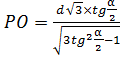

 

Ответ: высота пирамиды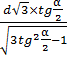

Заключение

 

Используя алгебраический метод решения геометрических задач мы использовали совокупность приемов по использованию алгебраических действий, формул, уравнений для решения данной задачи.

Мы определили, что с помощью алгебраического метода решения геометрических задач на построение легче определить условие возможности существования решений данной задачи, выявить их количество, а также особенности каждого решения.

Алгебраический метод дал возможность свести задачи геометрического содержания к решению и исследования алгебраических уравнений. Своей идеей метода координат Р. Декарт установил связь между геометрическими объектами и числами, которые и характеризуют. Тем самым с помощью метода координат Р. Декарт вывел алгебраический метод.

Цель решения задач геометрических задач алгебраическим методом состоит в том, чтобы с помощью формул и уравнений установить зависимость между данными и искомыми элементами фигуры.

С помощью алгебраического метода мы выделяли неизвестные элементы, к нахождению которых сводится задача. На основе данных условия задачи и известных теорем по геометрии выразили взаимосвязи между данными и искомыми элементами в виде уравнения. Таким образом получили алгебраические выражения, по которым выполняется построение или определение искомых элементов.

Из этого следует, что с помощью алгебраического метода решения геометрических задач мы значительно облегчаем задачу нахождения искомых элементов, используя совокупность приемов по использованию алгебраических действий, формул, уравнений и формул для решения поставленной задачи.

Список использованной литературы

 

1.                 Атанасян Л.С. и др. Геометрия: Учеб. для 10–11 кл. сред. шк./Л.С. Атанасян, В.Ф. Бутусов, С.Б. Кадомцев и др.– 14–е изд.– М.: Просвещение, 2005.–200с.

2.                 Ахмарова И.Н. Методы решения задач на построение в программе «Живая геометрия» / И.Н. Ахмарова // VI Русановские чтения: Всероссийская научно-практическая конференция имени В.Н. Русанова (г. Оса, 20 октября 2016 г.). [Электронный ресурс]. Вып. 6 / под общей редакцией Т.В. Сапожниковой. – МБОУ ДПО «Осинский методический центр». – СПб.: Изд-во «Маматов», 2016. – 56,9 М.

3.                 Ахмарова И.Н. Решение задач на построение методом инверсии с использованием программы «Живая геометрия» / И.Н. Ахмарова // Вопросы математики, ее истории и методики преподавания в учебноисследовательских работах: мастер. всерос. науч.-практ. конф. студентов  матем. фак-тов / ред. кол.: И.В. Косолапова; А.Ю. Скорнякова, под общ. ред. А.Ю. Скорняковой; ПГГПУ – Пермь, 2018. – Вып. 11. – 80 с.

4.                 Белошистая, А.В. Задачи на построение в школьном курсе геометрии / А. В. Белошистая // Математика в школе. – 2002. – №9. – С. 47-50.

5.                 Блинков А.Д. Геометрические задачи на построение / А.Д. Блинков, Ю.А. Блинков. – М.: МЦНМО, 2010. – 152 с.Бурда М.И. Решение задач на построение. М .: «Просвещение», 1986.-112 с.

6.                 Заславский А.А. Геометрические преобразования / А.А. Заславский. – М.: МЦНМО, 2004. – 86 с.

7.                 Исследовательские и проектные задания по планиметрии с использованием среды «Живая математика» / С.Г. Иванов, В.И. Рыжик. – М.: Просвещение, 2013. – 144 с.

8.                 Никулин Н.А. Геометрические построения в плоскости Лобачевского, ГИТЛ, 1991. - 164 с.

9.                 Погорелов A.B. Геометрия: учеб. для 7–9 кл. общеобразоват. учреждений / A.B. Погорелов. – М.: Просвещение, 2000. – 383 с.

10.            Сборник задач по геометрии, 5000 задач с ответами, Шарыгин И.Ф., Гордин Р.К., 2017 – 357 с.

11.            Ходот Т.Г. Задачи по геометрии : учеб. пособие для студ. высш. пед. учеб. заведений / Т.Г. Ходот, И.Д. Захарченко, А.Б. Михайлова. – М.: Академия, 2006. – 256 с.

12.            Шеремет Г.Г. Геометрические преобразования и фрактальная геометрия: учебник / Г.Г. Шеремет; ПГГПУ. – Пермь, 2013. – 188 с.Зетель С.И., Геометрия линейки и циркуля, М., 1950.- 308

 

Скачано с www.znanio.ru