
Анализ сетевых графиков включает решение следующих задач:
– определение времени выполнения комплекса работ (времени сетевого графика) – ТСГ;
– определение критических работ и критических путей;
– составление календарного плана;
– определение запаса времени (резерва) для работ проекта.
 |
В этом случае приняты при построении сетевого графика следующие обозначения (рис. 5): Аj – событие j – е; ТПi – самое позднее время начала работы аi-j; ТРi – самое раннее время начала работы аi-j; ТПj – самое позднее время окончания работы аi-j; ТРj – самое раннее время окончания работы аi-j. При этом работы ТПj и ТРj являются самым поздним и самым ранним временим начала последующей работы аj-k соответственно.
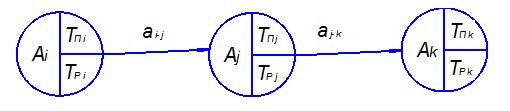
Рис. 5
Задача решается путем последовательного определения времен наступления всех событий сетевого графика. При решении этой задачи примем обозначения: аi-j – это работа, которая начинается после наступления события Аi и завершается наступлением события Аj, ti-j – время выполнения работы аi-j. С учетом сказанного, самое раннее время наступления (окончания) события определяется по формуле:
![]() , (2.1)
, (2.1)
где j – индекс рассматриваемого события Аj,, i – индексы всех предшествующих событий Аi, из которых можно перейти к событию Аj путем выполнения одной работы аij (за один шаг).
Самое позднее время наступления (окончания) события ![]() определяется по формуле:
определяется по формуле:
![]() , (2.2)
, (2.2)
где j – индекс рассматриваемого события Аj, k – индексы всех последующих событий Аk, в которые можно перейти из события Аj путем выполнения одной работы аjk (за один шаг). При этом в узлах графа указывают (рис. 4): номер события, самое раннее время начала (окончания) события и самое позднее время начала (окончания) события.
В качестве начала отсчета времени принимают момент начала выполнения комплекса работ Т1=0; формула (2.1) задает рекуррентную (последовательную) процедуру расчета моментов времени всех событий.
Покажем алгоритм решения на приведенном (рис. 3) примере.
Этап 1 Определяем самое ранние время наступления событий.
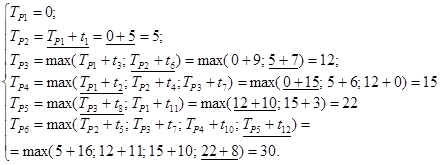 ;
;
Результаты расчета самого раннего времени наступления события записываем в нижнюю половину соответствующего узла графика (рис. 5).
Время сетевого графика ТСГ равно времени наступления последнего события сетевого графика, т. е. комплекс работ сетевого графика не может быть завершен ранее ТСГ.
ТСГ = Т6 = 30.
Таким образом, для выполнения комплекса работ требуется 30 единиц времени.
Этап 2 Определяем самое позднее время наступления событий. Расчет ведем с последнего события. Результаты расчета самого позднего времени наступления события записываем в верхнюю половину соответствующего узла графика (рис. 6).
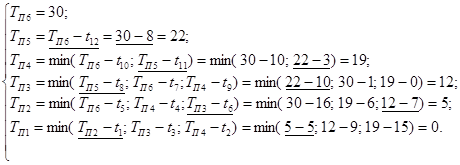
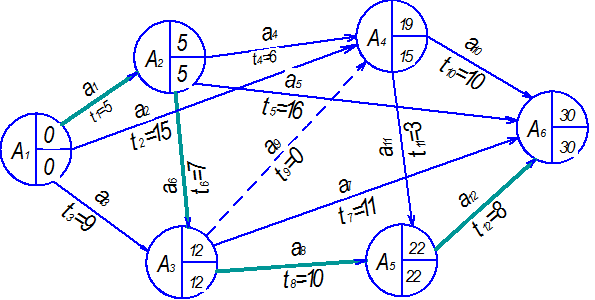
Рис. 6
Этап 3 Определяем критический путь.
Критическими называют работы, от времени выполнения которых зависит время выполнения сетевого графика.
Критический путь – это последовательность критических работ от первого до последнего события сетевого графика. Критических путей может быть несколько.
Критический путь состоит из критических работ, где для каждой работы должны соблюдаться три условия:
– время самого раннего начала i-й работы должно быть равно времени самого позднего начала работы: ТРi=TПi;
– время самого раннего окончания работы должно быть равно времени самого позднего окончания работы: ТРi+1=TПi+1;
– для каждой работы между моментом окончания работы и ее началом должны соблюдаться равенства: TПi+1= TПi+tj и TРi+1= TРi+tj.
Для нашего примера всем трем условиям удовлетворяют следующие работы: а1 ® а6 ® а8 ® а12. Они и являются поэтому критическими, образуя критический путь.
Особенностью критических работ является полное отсутствие запаса (резервного времени) для их выполнения. Запас времени характерен только для работ некритических путей и играет немаловажную роль в своевременном решении задач планирования и управления комплексами работ.
Этап 4 Составляем календарный план работ проекта.
Календарный план привязывают к конкретным датам начала и окончания комплекса в целом и всех работ, учитывающего выходные, праздничные дни, перерывы в работе по иным причинам и т.п.
В примере мы будем рассматривать условное время от некоторого начала отсчета Т1=0. Составление календарного плана начинают с критических путей и критических работ, которые не имеют резерва времени и безвариантно привязываются к плану работ (рис. 7), далее включают некритические работы и события.
Рис. 7
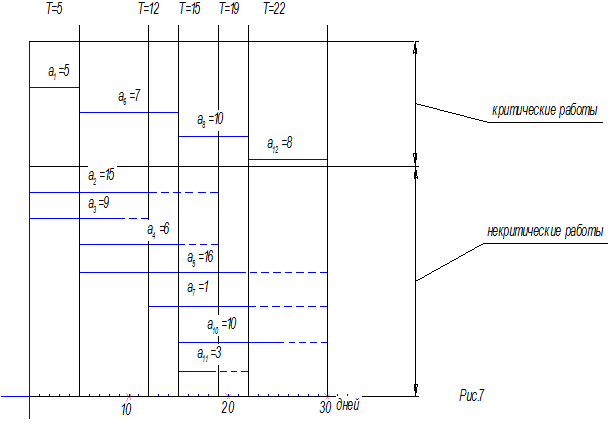
Из календарного плана видно, что некоторые работы имеют запас в выполнении (обозначенные пунктиром), т.е. резерв времени, которым по разному можно распорядиться. Поэтому включение в календарный план некритических работ представляет собой довольно сложную многовариантную задачу, не имеющую строгого алгоритмического решения. Ее обычно творчески решает руководство проекта. Однако, прежде чем решать вопрос о том, как лучше распорядиться имеющимися резервами времени, необходимо эти резервы времени рассчитать.
Этап 5 Определяем резерв времени для некритических работ.
Различают общий и свободный запас времени:
а) общий запас времени работы а i-j – это превышение над длительностью выполнения этого процесса интервала времени от самого раннего момента начала работа а i-j до самого позднего времени окончания этой работы, т.е.
D tOi-j= ТПj –TРi – t i-j;
б) свободный запас времени для некритической работы а i-j – это превышение над длительностью выполнения этой работы интервала времени – от самого раннего момента начала работы а i-j до самого раннего времени окончания этой работы, т.е.
DtСi-j= ТРj – TРi – ti-j.
При анализе резервов времени некритических работ необходимо помнить:
– если DtOi-j=DtСi-j (общий запас времени равен свободному), то работа аi-j может выполняться в любое время внутри своего максимального временного интервала (TPi, ТПj) без нарушения следования, где TPi – самое раннее время начала работы а i-j, ТПj – самое позднее время окончания работы а i-j.
– если DtСi-j < DtОi-j (т.е. свободный резерв меньше общего запаса), то работа аi-j без нарушения следования может начинаться со сдвигом, не превышающем DtСi-j, относительно самого раннего момента начала работы TРj. Сдвиг начала процесса на величину времени, превышающую DtСi-j, но не более DtОi-j, должен сопровождаться равным сдвигом относительно начала всех последующих за данным процессов.
Для нашего примера резерв времени для некритических работ равен (табл. 4):
Таблица 4
|
Некритические работы |
Длительность процесса |
Общий запас DtOi-j= ТПj-TРi- t i-j |
Свободный запас DtСi-j= ТРj-TРi- ti-j |
|
а2 |
15 |
19-0-15=4 |
15-0-15=0 |
|
а 3 |
9 |
12-0-9=3 |
12-0-9=3 |
|
а 4 |
6 |
19-5-6=8 |
15-5-6=1 |
|
а 5 |
16 |
30-5-16=9 |
30-5-16=9 |
|
а 7 |
1 |
30-12-1=17 |
30-12-1=7 |
|
а 10 |
10 |
30-15-10=5 |
30-15-10=5 |
|
а 11 |
3 |
22-15-3=4 |
22-15-3=4 |
Анализируя таблицу 4 резервов времени, можно сделать следующие выводы:
1 процессы а 3, а 5, а 10, а 11 могут выполняться в любое время внутри своих максимальных интервалов выполнения, т.к. DtOi-j=DtСi-j .
2 процессы а2, а 4, а 7 можно сдвигать относительно самого раннего времени начала этих процессов не более чем на DtСi-j. Сдвиг начала этих процессов на величину времени , превышающуюDtСi-j, но не болееDtOi-j, должен сопровождаться равным сдвигом всех последующих процессов. Например, для процесса а 4: самое раннее время его начала мы можем сдвинуть наDtСi-j.=1 день, однако в случае необходимости мы можем сдвинуть начало этой работы на интервал от двух до восьми дней (DtOi-j =8),но с последующим сдвигом самого раннего начала всех последующих работ на это же количество дней.
Упражнение. Составить календарный план при сдвиге работ на величину времени более DtСi.
Как лучше распорядиться этими резервами времени? Здесь могут быть самые разнообразные соображения. Чаще всего предлагается планировать работы таким образом, чтобы одновременно выполнялось возможно меньшее число работ и обеспечивалась более равномерная загрузка оборудования и персонала. Возможны и другие подходы. Например, все резервы оставить на завершение работ, чтобы гарантировать своевременность их выполнения в случае сбоев в работе. Можно наоборот, начинать выполнять работы возможно позже, чтобы сокращать объем незавершенного производства. Не исключены и другие соображения, например, сезонные изменения условий работы, отпускной период для персонала.
На рис. 8 представлен календарный план для рассматриваемого примера в условном времени. План составлен по принципу возможно более равномерного распределения работ во времени. Только в течение пяти единиц времени (11–15 и 19–20) предусмотрено параллельное выполнение четырех работ, все остальное время одновременно выполняется три работы.
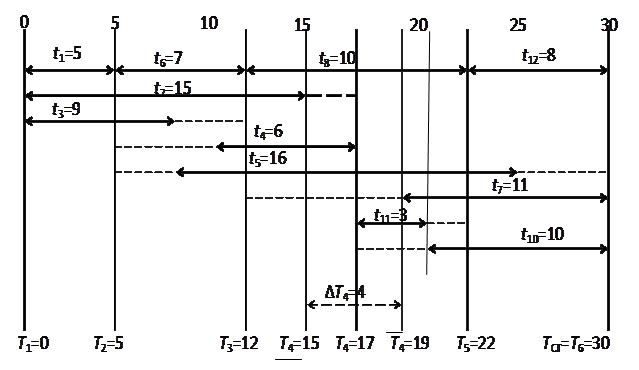
Рис. 8
Упражнения
Задан сетевой график. Определить критический путь, время выполнения сетевого графика. Составить календарный план.

1) t1=4; t2=7; t3=9; t4=5;
t5=12; t6=15; t7=11; t8=3.

2) t1=11; t2=14; t3=5;
t4=8; t5=6; t6=2; t7=3; t8=7.

3) t1=7; t2=13; t3=9; t4=4;
t5=10; t6=5; t7=8; t8=6.
4) t1=6; t2=18; t3=11; t4=4;
t5=7; t6=2; t7=5; t8=9.

5) t1=5; t2=15; t3=6; t4=15;
t5=3; t6=10; t7=2; t8=4.
6) t1=2; t2=10; t3=7; t4=12;
t5=9; t6=4; t7=5; t8=3.
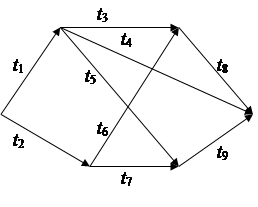
7) t1=5; t2=9; t3=3; t4=14;
t5=10; t6=4; t7=2; t8=7; t9=6.

8) t1=5; t2=7; t3=11; t4=4;
t5=13; t6=6; t7=5; t8=10; t9=2.
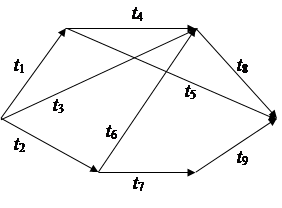
9) t1=11; t2=17; t3=19; t4=7;
t5=13; t6=8; t7=10; t8=12; t9=6.

10) t1=9; t2=10; t3=16; t4=18;
t5=7; t6=9; t7=6; t8=10; t9=12.
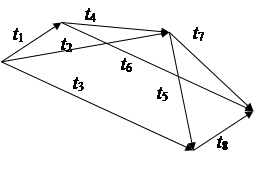
11) t1=8; t2=12; t3=7; t4=9;
t5=5; t6=20; t7=10; t8=6.

12) t1=6; t2=10; t3=12;
t4=2; t5=2; t6=3; t7=9; t8=8.

13) t1=3; t2=17; t3=10; t4=9;
t5=5; t6=7; t7=11; t8=4.
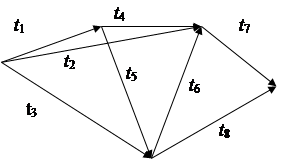
14) t1=4; t2=7; t3=10; t4=12;
t5=5; t6=3; t7=11; t8=15.

15) t1=8; t2=5; t3=10; t4=18;
t5=4; t6=3; t7=7; t8=16.
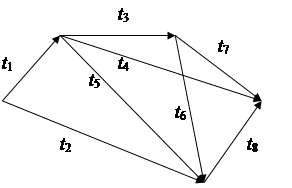
16) t1=12; t2=10; t3=2; t4=7;
t5=18; t6=2; t7=12; t8=6.

17) t1=2; t2=7; t3=5; t4=9;
t5=10; t6=6; t7=4; t8=8; t9=3.

18) t1=8; t2=4; t3=5; t4=10;
t5=12; t6=7; t7=3; t8=2; t9=4.

19) t1=5; t2=6; t3=7; t4=10;
t5=11; t6=6; t7=9; t8=8; t9=11.

20) t1=10; t2=3; t3=15; t4=11;
t5=6; t6=12; t7=7; t8=8; t9=9.

21) t1=5; t2=3; t3=11; t4=2;
t5=6; t6=9; t7=7; t8=4.

22) t1=3; t2=5; t3=8;
t4=12; t5=7; t6=4; t7=10; t8=10.
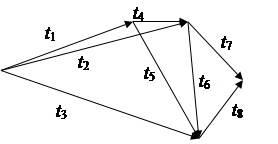
23) t1=8; t2=4; t3=12; t4=6;
t5=5; t6=10; t7=11; t8=7.

24) t1=10; t2=4; t3=12; t4=7;
t5=3; t6=2; t7=6; t8=9.
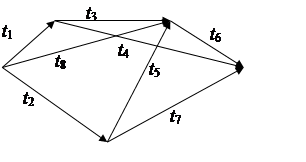
25) t1=7; t2=11; t3=4; t4=8;
t5=6; t6=9; t7=17; t8=10
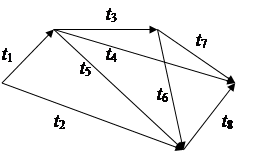
26) t1=5; t2=17; t3=8; t4=20;
t5=10; t6=9; t7=4; t8=8.

27) t1=10; t2=5; t3=6; t4=8;
t5=1; t6=7; t7=9; t8=2; t9=4.

28) t1=11; t2=8; t3=10; t4=4;
t5=8; t6=15; t7=9; t8=12; t9=14.
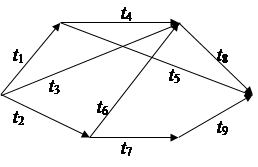
29) t1=8; t2=7; t3=10; t4=5;
t5=9; t6=3; t7=4; t8=2; t9=6.

30) t1=2; t2=4; t3=3; t4=7;
t5=5; t6=11 t7=10; t8=15; t9=4.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.