«Арифметическая прогрессия»

Методические аспекты изучения теоретического материала темы «Арифметическая прогрессия»

 

В учебниках алгебры для 9 класса дается следующее определение: «арифметической прогрессией называют последовательность, каждый член которой, начиная со второго, равен предыдущему члену, к которому прибавляют одно и то же число. Это постоянное для данной последовательности число d называют разностью арифметической прогрессии».

На этом этапе учителю следует привести как можно больше числовых последовательностей, с которыми ученики могут встречаться в повседневной жизни, а также при изучении основ наук. Таким образом учеников подготавливают к восприятию мысли о том, что предметом изучения математики является не только выражения, уравнения, неравенства и тому подобное; математика изучает также результаты наблюдений за реальными физическими, химическими процессами, климатическими явлениями, которые выражаются в виде рядов чисел, каждое из которых стоит в этой записи на строго определенном месте. После этого вполне логично сформулировать задачи: изучить вопрос об этих «ряды чисел», а также возможности дальнейшего применения этих понятий на практике. Таким образом формулируется в общем виде основная дидактическая цель.

Для осознания учениками необходимости выделения и дальнейшего изучения свойств последовательностей, можно предложить им выполнить упражнение на сравнение или логическое упражнение на исключение лишнего.

 

После выполнения таких упражнений учащиеся осознают, что среди бесконечного количества различных по видам числовых последовательностей, можно выделить (по другим критериям) другие виды. Среди них отдельно стоящие последовательности, в которых последующий член равен предыдущему члену, прилагаемом к тому же числу. После такого умозаключения формулируется основная дидактическая цель урока: изучить определения, дать название и исследовать свойства таких последовательностей и их применения.

Изучение материала урока начинается с формулировки определения арифметической прогрессии (учащиеся подготовлены к его восприятию на предыдущем этапе урока), в котором следует обратить внимание учащихся на словосочетание «начиная со второго», а также на то, что число, которое добавляется к каждому члену, начиная со второго, является постоянным для данной арифметической прогрессии, при этом оно может быть каким угодно (положительным или отрицательным; целым или дробным, оно может равняться даже 0, это желательно проиллюстрировать большим количеством примеров). После этого формулируется представление о содержании понятия «разность арифметической прогрессии» и записывается соответствующая формула. Далее традиционно записывается рекуррентная формула арифметической прогрессии, которая напрямую следует из определения арифметической прогрессии.

Для решения многих прикладных задач важны свойства арифметической прогрессии, в частности характеристическая свойство (хотя программа по математике не дает ее среди обязательных знаний в этой теме). Также обязательным, однако интересной для применения является теорема о задания арифметической прогрессии формуле a_n = k_n + b, где k, b - некоторые числа. Поэтому, если позволяют особенности класса, можно предложить названные свойства арифметической прогрессии рассмотреть как дополнительный материал.

Введение свойств арифметической прогрессии удобнее показать на конкретных примерах, а затем записать в общем виде.

Например, в арифметической прогрессии 1, 3, 5, 7, 9; ... каждый член, начиная со второго, является средним арифметическим двух соседних с ним членов:

 3 ₌ ; 5 ₌ ; 7 ₌  ;

Покажем, что такое свойство имеет любая арифметическая прогрессия. Пусть имеем арифметическую прогрессию (а_n) с разницей d. Тогда для натуральных значений n > 1 выполняются равенства :

 a_n – a_n–1 = d, a_n+1 – a_n = d.

Откуда: a_n – a_n–1 = a_n+1 – a_n;

 2a_n = a_n–1 + a_n+1;

 a_{n =  .}

Свойство 1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов. С этим свойством арифметической прогрессии и связано ее название.

Рассмотрим конечную арифметическую прогрессию (x_n ), которая имеет 7 членов: 3; 5, 7, 9; 11; 13; 15. Найдем сумму крайних членов прогрессии и суммы членов, равноудаленных от крайних:

x₁ + x₇ = 3 + 15 = 18;

 x₂ + x₆ = 5 + 13 = 18;

 x₃ + x₅ = 7 + 11 = 18;

 x₄ + x₄ = 9 + 9 = 18.

Сумма любых двух членов арифметической прогрессии, которые равноудалены от ее крайних членов равна сумме крайних членов.

Используем эти соображения для произвольной конечной арифметической прогрессии a₁; a₂; …; a_n с разницей d. Пусть a₁ + a_n = m. тогда:

 а₂ + а_n-1 = (a₁+d) + (a_n – d) = a₁+a_n = m;

а₃ + а_n-2 = (a₂+d) + (a_n-1 – d) = a₁+a_n = m и т.д.

 Свойство 2. Сумма любых двух членов конечной арифметической прогрессии, которые равноудалены от ее крайних членов равна сумме крайних членов этой прогрессии. (Рис. 1)

 

После введения понятия арифметической прогрессии учеников приводят к формуле n - го члена и формул суммы первых членов прогрессии. Формулу n-го члена арифметической прогрессии получают в 9 классе индуктивным методом использовав неполную индукцию. Сначала вспоминают способ задания арифметической прогрессии, потом убеждаются, что он неудобен для поиска членов прогрессии. Известно a_n+1 = a_n + d.

Учащимся предлагается найти несколько членов арифметической прогрессии в которой a₁=4, d=3. Оказывается, что, например, a₅₀ неудобно находить, используем метод неполной индукции и составим следующие равенства:

а₂ = a₁ + d,

a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2d,

a₄ = a₃ + d = (a₁ +2 d) + d = a₁ + 3d,

… … … … … … … … … … … … … …

a_n = a₁ +(n – 1) d.

Этот метод приводит к формуле n-го члена прогрессии, но не является строгим доказательством.

При решении упражнений кроме закрепления терминологии и формул, выражающих свойства, проводится отработка таких ключевых моментов: как проверить, является ли заданная последовательность арифметической прогрессией (по определению, или характеристической свойством, или по теореме, в зависимости от условия); как найти разницу арифметической прогрессии (от любого члена, начиная со второго, отнять предшествующий него член) как найти член, следующий за данным членом арифметической прогрессии (найти разницу арифметической прогрессии и добавить ее к данному члену).

Перед введением суммы первых n-членов арифметической прогрессии в общем виде рассматривают пример нахождения суммы натуральных чисел от 1 до 100.

Пример 1.

Найти сумму натуральных чисел от 1 до 100.

S = 1 + 2 + 3 + … + 98 + 99 + 100

+

 S = 100 + 99 + 98 + … + 3 + 2 + 1

 2S = 101 + 101 + 101 + … +101 + 101 + 101

 2S = 101 · 100

 S = 101 · 50 = 5050.

Этот же прием используют для вывода формулы суммы n-первых членов арифметической прогрессии. Из предыдущего примера ученики понимают, что в рассматриваемом примере

a₁ = 1; n = 100; d = 1.

В общем виде мы будем искать сумму S _n

S_n = a₁ + a₂ + a₃ + … + a_n-2 + a_n-1 + a_n

+

 S_n = a_n + a_n-1 + a_n-2 + … + a₃ + a₂ + a₁

Добавив полученные равенства получим

2S_n = (a₁ + a_n ) + ( a₂ + a_n-1 ) + ( a₃ + a_n-2 ) + … + ( a_n-1 + a₂ )+ ( a_n + a₁ ).

По свойству арифметической прогрессии сумма двух членов конечной арифметической прогрессии, равноудаленных от начала и конца, равна сумме первого и последнего членов, получим формулу

 S_n =  (1)

Вторую формулу для вычисления суммы получают подставив в формулу (1) формулу a_n = a₁ +(n – 1) d, получим

 S_n =  .

Для осознания учениками необходимости изучения формулы п-го члена арифметической прогрессии и дальнейшего ее применения можно предложить им выполнить такое упражнение: зная первый член и разность арифметической прогрессии, найти ее некоторое член (номер которого достаточно большим). Осознав нерациональность решения задачи известным ученикам способом (через применение рекуррентной формулы), они приходят к вопросу: не существует ли способа нахождения любого члена арифметической прогрессии без необходимости находить предыдущие несколько ее членов? Поиск ответа на этот вопрос - основная цель урока.

Например, можно начать работу с несложных упражнений:

Пример 2.

Дано конечная последовательность: (х_n): 3; 0; -3; -6; -9; -12. Укажите:

1) первый, третий, шестой члены этой последовательности;

2) является ли эта последовательность возрастающей, убывающей;

3) формулу ее n-го члена.

Решение.

1) первый член последовательности = 3, третий = -3, шестой = -12 ;

2) последовательность является убывающей, так как каждый последующий член меньше предыдущего.

3) формулу ее n -го члена (х_n) = 3 – 3n, где n = 0, 1, 2, ….

Пример 3.

Является ли последовательность чисел 3, 0; 3; -6; -9 арифметической прогрессией?

Решение.

Обозначим члены заданной последовательности: a₁ = 3; a₂ = 0; a₃ = –3; a₄ = –6; a₅ = –9. Найдем разности следующего и предыдущего членов последовательности:

a₂ – a₁ = 0 – 3 = –3; a₃ – a₂ = –3 – 0 = –3;

a₄ – a₃ = –6 – (–3) = –3; a₅ – a₄ = –9 – (–6) = –3.

Поскольку полученные разности равны одному и тому же числу 3, то эта последовательность является арифметической прогрессией.

Изучение материала урока начинается с вывода формулы суммы первых п членов арифметической прогрессии через первый и п-и члены, для чего используется свойство конечной арифметической прогрессии (о том, что сумма каждой пары членов, равноудаленных от ее концов, равна сумме крайних членов этой прогрессии) и довольно простые соображения о количестве пар чисел, содержащихся в ряде п чисел. Вторая формула для вычисления суммы первых п членов арифметической прогрессии через первый ее член и разность выводится с применением к выведенной формулы изученной ранее формулы п-го члена арифметической прогрессии. После изучения обеих формул следует отметить, что выбор формулы для решения конкретной задачи обусловлен данными задачи.

Пример 4.

Первый член арифметической прогрессии равен 3, а разность 2. Чему равен второй член этой прогрессии?

Решение.

Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Тогда каждый последующий член можно вычислить через предварительный по рекуррентной формуле a_n+1 = a_n + d.

Использовав рекуррентную формулу а₂ = а₁ + d получим:

а₂ = -3 + 2;

а₂ = -1.

Ответ: -1.

При решении упражнений учащиеся должны знать:

1. Определение арифметической прогрессии

2. Способ нахождения разности арифметической прогрессии.

3. Основные свойства арифметической прогрессии.

Пример 5.

В арифметической прогрессии а₁ = 4, d = 3. Найдите а₂₀.

Решение.

а₂₀ = а₁ + 19d = 4+ 19·3 = 61.

Ответ 61.

Необходимо предложить учащимся решить другие задачи для закрепления уже изученных, определения и формулы, а также для выработки оперативных умений по применению формул при решении задач в различных ситуациях.

Пример 6.

Найти девятый член арифметической прогрессии (a_n): 5; 4,2; 3,4; ... .

Решение.

Имеем: a₁ = 5.

Найдем разницу прогрессии: d = 4,2 – 5 = –0,8.

Тогда, a₉ = a₁ + 8d = 5 + 8 · (–0,8) = –1,4.

Ответ: -1,4.

 Содержание упражнений и цель, которой добивается учитель при решении этих упражнений, такие же, как и на предыдущем уроке: закрепление определения и формулы, изученных на этих уроках, а также выработки оперативных умений по применению формул при решении задач в различных ситуациях. (Если позволяют успехи учеников, повышается уровень сложности задач за счет задач на применение свойств арифметической прогрессии).

Пример 7.

Найти сумму первых девяти членов арифметической прогрессии (a_n): 3; 7;11;...

Решение.

1-й способ.

Имеем: a₁ = 3, d = a₂ – a₁ = 7 – 3 = 4.

Найдем а₉: a₉ = 3 + + 8 · 4 = 35. По первой формуле суммы первых n членов арифметической прогрессии через первый и n-й члены находим:

S₉ =  = 171.

2-й способ.

Зная, что a₁ = 3, d = 4, по второй формуле для вычисления суммы первых n-членов арифметической прогрессии через первый ее член и разность находим:

S₉ =  = 171.

Ответ. 171.

Пример 8.

Найти сумму нечетных натуральных чисел, не превышающих 71.

Решение.

Нечетные натуральные числа образуют арифметическую прогрессию 1, 3, 5 ..., в которой a₁ = 1, d = 2, a_n = 1 + (n – 1) · 2 = 2n – 1. Найдем, какой порядковый номер имеет член 71 этой прогрессии: 71 = 2n - 1; n = 36. Следовательно, нужно искать сумму первых тридцати шести членов прогрессии. Находим:

S =  · 36 = 1296.

Ответ. 1296.

Пример 9.

Найти первый член арифметической прогрессии (а_n), если сумма второго и двенадцатого ее членов равна 20,4, а сумма первых одиннадцати - 121.

Решение.

По условию имеем: a₂ + a₁₂ = 20,4; S₁₁ = 121. Используя формулы n-го члена и суммы первых n членов арифметической прогрессии, получим систему уравнений

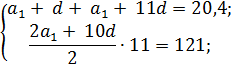
 Отсюда:

 

Ответ. 15.

Активизация познавательного интереса обучающихся достигается за счет введения прикладных задач связанных с арифметической прогрессией.

В биологии прогрессии связаны с такими темами, как размножение, деление клеток, форменные элементы крови и другие. Невозможно решить биологические задачи, не использовав знания о прогрессии. По теории эволюции Дарвина, все процессы, связанные с живыми организмами, происходят прогрессивно или регрессивно.

Пример 10.

Количество эритроцитов (из расчета на 1 мм³) в крови человека составляет на уровне моря - 5000000. Через каждые 600 м поднятия в гору их количество увеличивается на 1000000. Какое количество эритроцитов будет в крови человека, если он поднимется на вершину горы Эверест (4800 м).

Решение.

Проанализируем эту задачу. Составив математическую модель этой задачи мы получим, что количество эритроцитов в крови человека увеличивается по арифметической прогрессии.

Из условия нам дано a₁=5, d = 1, h = 4800, h₁ = 600. Нужно найти a_n.

Сначала найдем значение n.

n =  =  = 8

Подставим известные значения в формулу a_n = a₁ + (n – 1)d, получим

a₈ = a₁ + 1(n – 1) = 5 + 7 = 12 (млн).

Ответ 12 млн.

Задача связана с физикой.

Пример 11.

Тормозя, автомобиль за первую секунду проехал 15 м, а за каждый последующие - на 3 м меньше, чем за предыдущую. Найдите тормозной путь автомобиля.

Решение.

Для того, чтобы правильно решить задачу нужно внимательно прочитать условие. Мы увидим, что тормозной путь образует арифметическую прогрессию.

Из условия мы видим, что нам дано a₁ =15, d = -3, a_n = 0.

Нам нужно найти S_n - тормозной путь.

Сначала нужно найти п . Используем формулу a_n = a₁ + d(n – 1), получим

15 - 3 (n -1) = 0,

n = 6.

Теперь можем посчитать S_n - тормозной путь, использовав первую формулу отыскания суммы первых последовательных n-членов арифметической прогрессии .

S₆ =  · 6 = 15 · 3 = 45 (м) - тормозной путь автомобиля.

Ответ: 45 м.

При решении упражнений закрепляется знание формул и осознание различия ситуаций, в которых оправдано применение одной из изученных формул, а также формируются умения работать с изученными формулами в разных направлениях: как для отыскания значения суммы арифметической прогрессии, так и для отыскания по данной суммой других данных (первого члена арифметической прогрессии, или ее разницы, или количества первых членов, для которых известна их сумма). Кроме этого продолжается работа по закреплению ключевых моментов, над которыми началась работа на предыдущих уроках: как проверить, является ли заданная последовательность арифметической прогрессией (по определению, или характеристической свойством, или по теореме, в зависимости от условия); как найти разницу арифметической прогрессии (от любого члена, начиная со второго, отнять предшествующий него член) как найти следующий за данным член арифметической прогрессии (найти разницу арифметической прогрессии и добавить ее к данному члена).

Таким образом, при решении упражнений закрепляется знание формул и осознание разницы в ситуациях, в которых использование одной из изученных формул оправдано, а также умение работать с формулами изучены в разных направлениях: как для нахождения значения суммы арифметической прогрессии, так и для нахождения по заданной сумме других данных (первый член арифметической прогрессии, или ее разность, или число первых участников, для которых известна их сумма).

 

2.2. Система задач для углубленного изучения темы «Арифметическая прогрессия»

 

Для подготовки обучающихся к ОГЭ по математике нами разработана система задач для углубленного изучения темы «Арифметическая прогрессия».

Задача 1. Найти сумму 15 первых членов арифметической прогрессии, если ее третий член равен - 5, а шестой равен 2,2.

Решение

Определим сумму арифметической прогрессии S_n =

Найдем d - разность арифметической прогрессии:

, 3d = . Отсюда:

.

Найдем a_{1 :}

  

 Тогда S₁₅ =
         S₁₅ = 105

Ответ: 105.

Задача № 2. Сколько отрицательных членов имеет арифметическая прогрессия -28, -25, -22…

Решение

a_n - арифметическая прогрессия.

Если a₁ = - 28, a₂ = - 25, то d = a₂ - a₁ = - 25 – (-28) = -25 + 28 = 3,

a_n = a₁ + d(n-1)

a_n = -28 + 3(n-1)

Учитывая, что a_n  имеем: -28 + 3(n-1) _,

3n – 3 _,

3n _, n _.

Так как n є N, то n =10.

Ответ: 10.

Задача № 3. Найти первый член арифметической прогрессии, разность которой равна 15, а сумма ее первых тринадцати членов равна 1326.

Решение

a_n - арифметическая прогрессия.

d - разность арифметической прогрессии, d = 15.

По условию S₁₃ = 1326,

S₁₃ = , 1326 =

1326 = (a₁ + 6d) 13, 102 = a_{1 +} 6d.

Так, как d = 15 , то 102 = a₁ + 6 15, a₁ + 90 = 102, a₁ = 102 – 90, a₁ = 12.

Ответ: 12.

Задача № 4. Найти разность и первый член арифметической прогрессии, если a₄ = 1,8, a₇ = 0,6

Решение.

Исходя из условия задачи составляем систему уравнений и решаем ее:

Решим систему уравнений способом сложения, умножив первое уравнение на (-1). имеем: Тогда 1,2 = -3d, d = 1,2: (-3), d = -0,4.

Тогда a₁ = 0,6 – 6d, a₁ = 0,6 – 6·(-0,4) = 0,6 + 2,4 = 3.

Ответ d = - 0,4;           a₁ = 3.

 

Задача № 5. Первый член арифметической прогрессии равен 2, а ее разность равна 5. Сколько надо взять первых членов прогрессии, чтобы их сумма была равна 156?

Решение

Сума арифметической прогрессии определяется по формуле:

S_n =

где n є N. Известно, что а₁=2, а d=5, S=156.

156 =  312 = (4+5n-5)·n, 5n² – n – 312 = 0,

D = 1 + 5 · 4 · 312 = 6241, .

n₁ = ,                n₂ = ,

n₁ не удовлетворяет условию n є N.

Ответ: 8.

Задача № 6. Сумма n первых членов арифметической прогрессии вычисляется по формуле . Найдите шестой член этой прогрессии.

Решение

 

3;

d =

Ответ: - 5.

Задача № 7. Найдите сумму всех чисел, кратных 6 и меньше 250.

Решение

Последовательность чисел, указанных в условии, образуют арифметическую прогрессию, в которой  

Известно, что

,

,

6n,

n,

n

n,

n є N

Количество членов этой прогрессии: n=41.

Ответ: 5166.

Задача № 8. Найдите сумму всех трехзначных чисел, меньших 250, которые кратны 3.

Решение

Указанные числа образуют арифметическую прогрессию, первый член которой = 102, разность d=3, n-й член = 102+3(n-1)=3n+99. Найдем количество членов прогрессии: 3n 

n є N, значит, нужно найти сумму 50 чисел. Имеем:

Ответ: 8775.

Задача № 9. Найдите сумму пятнадцати первых членов арифметической прогрессии, восьмой член которой равен 8.

Ответ: 120.

Задача № 10. Найдите сумму всех трехзначных чисел, кратных 12.

Решение

Числа, кратные 12, образуют арифметическую прогрессию с разностью 12 первый член которой равен 108. Больше цифровыми число, которое делится на 12, есть число, которое делится на 2 и на 3 и меньше 1000. Таким числом является число 996. Найдем номер члена этой прогрессии, равный

996: 996 = 108+12 ( n-1),        108+12 n-12 = 996,

12 n = 996 - 96, 1  2 n = 900,

n = 900:12, n = 75.

То есть, последнее цифровыми число, кратное 12 является 75-м членом этой прогрессии,

Ответ: 41 400.

Задача № 11. Два тела, которые находились на расстоянии 153 м движутся навстречу друг другу. Первый движется со скоростью 10 м в секунду, а второй за первую секунду прошел 3 м, а за каждую следующую секунду на 5 м больше, чем за предыдущую. Через сколько секунд они встретятся?

Решение.

Пусть тела встретятся через х секунд.

Тогда первый предмет прошел расстояние 10 х м, а второй - путь, равный сумме членов арифметической прогрессии

S = 3+(3+5)+(3+5·2)+…+(3+5(x-1))

По условию задачи: 10x +S = 153,

                            10x + ,

                            5x²+21x-306=0,   x=6

Ответ: 6 с.

Задача № 12. Могут числа, выражающие длины сторон треугольника и его периметр, образовывать арифметическую прогрессию?

Решение

Предположим, что числа, выражающие длины сторон треугольника. образуют арифметическую прогрессию:

a, a+d, a+2d.

Тогда периметр этого треугольника будет равен:

P = a+a+d+a+2d,

P = 3a+3d.

Найдем разность между периметром и самой большой стороной6

(3a+3d)-(a+2d) = 2a+d,

так, как 2a+d>d, то периметр не является четвертым членом арифметической прогрессии

Задача № 13. Телеграфные столбы ставят на расстоянии 50 м друг от друга. Выразить длину линии связи L_n в зависимости от количества поставленных столбов

Решение

L_n = 50 (n – 1).

Если n = 2, 3, 4, 5,….,

то L₂ = 50м, L₃ = 100 м, L₄ = 150 м, L₅ = 200 м…

Задача № 14. Решить уравнение 3 + 7 + 11 +…..+ x = 820

a₁ = 3, a₂ = 7, a₃ = 11, a_n = x - члени возрастающей арифметической прогрессии (a_n, где d = a₂ - a₁ = 7 – 3 = 4.

Найдем количество членов прогрессии:

a_n = a₁ + (n – 1) d,          n–1 = ,        n = ,

n = ,                   n =

Найдем сумму членов арифметической прогрессии:

S_n =                  S_n = .

Значит ,

x²+4x+3=6560,

x²+4x – 6557=0,

D =16+26228=26244   

x₁=                   x₂=

Ответ6 79.

Задача № 15. Найти сумму 19 первых членов арифметической прогрессии a_n, если известно, что a₄ + a₈ + a₁₂ + a₁₆ = 224.

Решение

S_n = .

Тогда S₁₉ =   = =19.

По условию a₄ + a₈ + a₁₂ + a₁₆ = 224, тогда

a₁ + 3d + a₁ + 7d + a₁ + 11d + a₁ + 15d = 224,

4a₁ + 36d = 224,

4 (a₁ + 9d) = 224,

a₁ + 9d = 56.

откуда, S₁₉ =(a₁ + 9d)·19 = 56 · 19 = 1064.

Ответ: 1064.

Задача № 16. Четвертый член арифметической прогрессии равен 9, а девятый - 6. Сколько нужно взять членов, чтобы их сумма была равна 54?

Решение

a_n - арифметическая прогрессия, по условию a₉=-6

a₉= a₁+8d, a₁+8d=-6,

a₄= 9 или a₄= a₁+3d,     a₁+3d=9.

Составим систему и решим ее:

 

                                      _______________________

                                                5d = -15

                                                d = -3

Тогда 9 =

 9 =

Учитывая, что сумма n членов равна 54, имеем:

54=,

108=(36-3n+3)n,

36=(13-n)n,

n²-13n+36=0,

n₁=4 n₂=9

оба корня удовлетворяют условию задачи, о чем свидетельствует проверка 18, 15, 12, 9, 6, 3, 0, -3, -6. S₄=54.

S₉= S₄+0=54, так как сумма последних членов равна нулю.

Ответ: 4, 9.

Задача № 17. Между членами 8 и 20 вставить семь цифр, которые вместе с данными будут образовывать арифметическую прогрессию. Обобщить решение.

Решение

Пусть a_n - арифметическая прогрессия. По условию a₁=8, a₉=20

Тогда a₉ = a₁ + (9-1)d,

a₉ = a₁ + 8d,

20 = 8 + 8d,

8d = 20 - 8,
         8d = 12,

d = 1,5

Значит a₁ =8, a₂ = a₁+d =8+1,5=9,5, a₃ = a₂+d = 9,5+1,5=11,

a₄ =12,5, a₅ =14, a₆ =15,5, a₇ =17, a₈ =18,5, a₉ =20

Вывод: Если нужно вставить К средних арифметических между членами a і b, то имеем b=a+(K+1)d, d=.

Если известны а₁ і d, то можно определить другие члени прогрессии.

Задача № 18. Дано прогрессию 2,1; 3,3; 4,5; ... Вычислить номер члена прогрессии, который равен 11,7.

Решение:

Итак это арифметическая прогрессия, разность которой d=1,2.

Ответ: Данное число является девятым членом арифметической прогрессии.

Задача № 19. В арифметической прогрессии а₅=14,91; а₉=20,11. Вычислить а₁.

Решение:

Составим систему уравнений и решим ее.

.

Ответ: .

Задача № 20. В арифметической прогрессии а₇=12,01; а₁₁=17,61. Вычислить разность прогрессии.

Решение:

Составим систему уравнений и решим ее.

Ответ:.

Задача № 21. В арифметической прогрессии а₉+а₁₅=14,8. Вычислить а₁₂.

Решение:

Ответ: .

 

Задача № 22. Вычислить первый член арифметической прогрессии, если сумма первых двенадцати членов равна 642, а двенадцатый член равен 48.

Решение:

 Ответ:.

Задача № 23. В арифметической прогрессииа₉=12,4; а₂₃=4,7. Найти а₁₄+а₁₇.

Решение:

В арифметической прогрессии суммы равноудаленных членов равны.

Ответ:.

Задача № 24. Сумма п первых членов арифметической прогрессии выражается формулой . Найти а₆.

Решение:

Найдем  і .

Ответ:.

Задача № 25. Сумма п первых членов арифметической прогрессии выражается формулой . Найти разность прогрессии.

Решение:

Ответ:.

Задача № 26. В арифметической прогрессии Найти .

Решение:

Ответ:.

Задача № 27. В арифметической прогрессии. Вычислить .

Решение:

Ответ:.

Задача № 28. Определить число сторон многоугольника, у которого число градусов, содержащийся в последовательных внутренних углах его, составляет арифметическую прогрессию с первым членом 120^о и разницей 5^о.

Решение.

Сумма внутренних углов выпуклого многокутникa вычисляется по формуле 180⁰(n – 2).

S_n = 180⁰(n – 2).

S_n = ,

180(n – 2) = ,

(235 + 5n)n = 360( n – 2),

n² – 25n + 144 = 0, n = 16 або n = 9.

Ответ: 9 или 16 сторон.

Задача № 29. Сумма первых 3-х цифр, составляющих арифметическую прогрессию равна 12, а сумма квадратов этих же чисел равна 66. Найти эти числа.

 Решение:

а₁ + а₂ + а₃ = 12 имеем 3а₁ + 3d = 12, а₁ + d = 4, а₁ = 4 - d

а₁² + а₂² + а₃² = 66,

Возведем 1-е уравнение в квадрат (а₁ + а₂ + а₃)²

а₁² + а₂² + а₃² + 2(а₁а₂ + а₁а₂ + а₂а₃) = 144

 

2 (а₁а₂ + а₁а₃ + а₂а₃) = 78,

а₁а₂ + а₁а₃ + а₂а₃ = 36,

а₁ (а₁ + d) + а₁ (а₁ + 2d) + (а₁ + d) (а₁ + 2d) = 39,

4 (4-d) + (4-d) (4 + d) + 4 (4 + d) = 39,

16 - 4d + 16 - d² + 16 + 4d = 39,

- d² + 48 = 39,

d² = 9, d = ± 3,

если d = -3 d = 3,

 а₁ = 4 - (- 3) = 7 а₁ = 4-3 = 1,

 а₂ = 4 а₂ = 4,

 а₃ = 1 а₃ = 7.

Ответ: 1; 4, 7 или 7; 4, 1.

Задача № 30. Определить восьмой член возрастающей арифметической прогрессии если а₂+а₇=18, а₂ × а₇=56.

Решение. Выразим из первого уравнения а₂ и подставим во второе

a₂=18-a₇; (18-a₇) a₇=56.

Раскрываем скобки и сводим к квадратному уравнению

а₇² – 18а₇ + 56 = 0

С помощью дискриминанта вычисляем неизвестный член прогрессии

D = (-18)² - 4×56 = 100

 

Из первого условия делаем вывод, что только при a₇ = 14 арифметическая прогрессия будет растущей.

Соответственно a₂=18-a₇=18-14=4.

По формуле a₇=a₂+5d

Определяем шаг прогрессии

14=4+5d; 10=5d; d=2.

Находим 8 член арифметической прогрессии

a₈ =a₇+d=14+2=16.

Для самопроверки можно подставить полученные значения в условие задачи.

Ответ: a₈ =16.

Задача № 31. Вычислить сумму первых восьми членов убывающей арифметической прогрессии если а₂ + а₆ = 24 а₂ × а₆ = 128.

Решение. Чтобы найти сумму прогрессии нам нужно знать первый и восьмой член прогрессии, или 1 член прогрессии и разность. Для начала определим из двух уравнений хотя бы один член прогрессии

а₂ = 24 - a₆;

(24-a₆) × a₆ = 128.

При раскрытии скобок получим квадратное уравнение

a₆² – 24a₆ + 128 = 0

По стандартной схеме посчитаем дискриминант

D = (-24)² - 4× 128 = 64

и 6 член арифметической прогрессии

При a₆ = 8 арифметическая прогрессия является убывающей. Находим разность прогрессии

a₂ = 24-a₆ = 24-8 = 16.

a₆ = a₂ + 4d = 16 + 4d = 8;

4d = -8; d = -2.

Легко заметить, что значение второго члена прогрессии всегда совпадает с корнем уравнения, который отвергаем по условию задачи. Это своего рода подсказка правильности вычислений. Находим первый и восьмой член прогрессии

a₁ = a₂ -d = 16 - (- 2) = 18;

a₈ = a₆ + 2d = 8 + 2 × (- 2) = 4.

Найденные значения подставляем в формулу суммы арифметической прогрессии

S = (a₁ + a₈) × 8/2 = (18 + 4) × 8/2 = 88.

Ответ: Сумма восьми членов прогрессии равна 88.

 

Скачано с www.znanio.ru