Бақылау жұмысы 10 сынып

11.05.16ж        Алгебра 10б

Сабақ жоспары

Сабақтың тақырыбы: Тригонометриялық теңсіздіктерге есептер шығару

Сабақтың мақсаты: Оқушылар теңсіздіктің жаңа түрі – тригонометриялық теңсіздіктер және оны шешу жолдарын үйрену, қарапайым теңсіздіктердің барлық түрімен, олардың шешімінің бар және жоқ болу шарттарын есеп шығару кезінде есте ұстау; тригонометриялық теңсіздіктерді  шешу алгоритмін білу, оны есеп шығаруға қолдану білік, дағдыларын қалыптастыру.  

Түрі: жаттығу, пысықтау сабағы

Типі: практикалық

әдісі: сұрақ-жауап

Сабақтың барысы:

 І.Ұйымдастыру оқушыларды  түгендеу, сабаққа әзірлігін тексеру

 ІІ.  Үй жұмысын тексеру:

1.     4 оқушыға карточка беру

Карточка№1. 1. Өнектің мәнін тап:   arcsin ( - √2/2) +  П  /4

                        2. Теңсіздікті шеш: tg(x - П / 10 )>1

 

Карточка№2.  1. Өнектің мәнін тап:  5/П* arcsin √3/2 + 1/6

                        2. Теңсіздікті шеш: 2 sin(x - П /3)>1

 

Карточка№3. 1. Өнектің мәнін тап:   arctq ( - 1 ) +  П  /4

                        2. Теңсіздікті шеш:    ctg x -√3 <0

 

Карточка№4. 1. Өнектің мәнін тап:   arcctq√3    +  П

                        2. Теңсіздікті шеш:    cos² 2x – sin² 2x<0

Қалған оқушылардан ауызша қайталау: сұрақтар арқылы өткізу:

А) тригонометриялық функциялардың қасиеттері графигі

ә) тригонометриялық теңдеудің түбірлерінің формулалары

б)  қарапайым тригонометриялық теңдеудің түбірлерінің формулалары

 в) кері тригонометриялық функциялардың қасиеттері

г)  тригонометриялық теңдеудің түбірлерінің дербес жағдайдағы түбірлерінің     

     формулалары

2.     есептерін тексеру, түсінбеген сұрақтарды талдау;

3.     оқылған тақырып бойынша қайталау яғни, қарапайым теңсіздіктердің барлық түрімен, олардың шешімінің бар және жоқ болу шарттарын  қайталау;

  ІІІ. Сабақта орындалатын есептер

1. Тригонометриялық теңсіздіктердің шешімдерінің формулалары:

sinx<a   ↔   -π-arcsina+2πk < x < arcsina+2πk

sinx>a   ↔   arcsina+2πk < x < π-arcsina+2πk

cosx<a   ↔   arccosa+2πk < x < 2π-arccosa+2πk

cosx>a   ↔   -arccosa+2πk < x < arccosa+2πk

tgx>a     ↔   arctga+πk < x < π/2+πk

tgx<a     ↔   -π/2+πk < x < arctga+πk

ctgx>a     ↔  πk < x < arcctga+πk

ctgx<a     ↔   arcctga+πk < x < π+ πk

 №1

   теңсіздігін шешіңіз.

 

№2

Функцияның периодтығына мысал.

Синус, косинустың ең кiшi оң периоды   2p.

Тангенс, котангенстың ең кiшi оң периоды   p.

Егер f функциясы период Т болса, онда  Af(kx+b) функциясының периоды  T/|k| санына тең

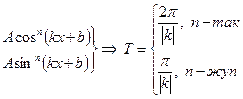
Егер функция екі немесе бірнеше функциялардың қосындысынан тұрса, онда оның периоды құрамындағы функциялардың периодтарының ең кіші ортақ еселігіне тең болады.

 

 №3

 функциясының ең кіші оң периодын тап.

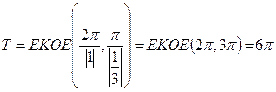
№4

 Иррационал  теңсіздіктерге мысал.

Иррационал  теңсіздіктердің формулалары:

 

 

 

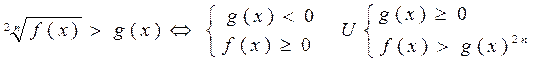
 №5

   теңсіздігін шешіңіз.

 

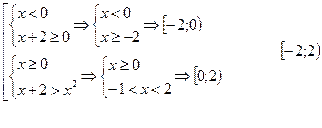
Қорытынды

Үй тапсырмасы: Тестпен жұмыс

Бағалау

 

 

 

 

 

 

11.05.16ж           Алгебра 8

Сабақ жоспары

Сабақтың тақырыбы: Квадрат теңсіздіктерді парабола әдісімен шешу

Сабақтың мақсаты:

Білімділік: Оқушыларға квадраттық теңсіздікті шешуде функцияның графигін қолдану      тәсілін меңгерту.

Дамытушылық: Есептер шығаруда тиімді тәсілді қолдану, ойлау, есте сақтау қабілеттерін   арттыру.

Тәрбиелік: Оқушыларды өзін-өзі басқаруға, ұйымшылдыққа, ұқыптылыққа, дәлдікке, өз  мүмкіндігіне сенуге, үлкен жетістікке ұмтылуға тәрбиелеу.

Сабақтың түрі: Сайыс сабақ

                            «Не? Қайда? Қашан?» телеойыны

Сабақтың әдісі: Танымдық ойын, тест, сұрақ-жауап, деңгейлеп оқыту

Сабақтың барысы:

І. Ұйымдастыру. Оқушыларды  түгендеу, сабаққа әзірлігін тексеру

«Не? Қайда? Қашан?» телеойыны барысында сырттан келген тапсырмаларды орындау.

ІІ.Үй тапсырмасын тексеру

1.      Еске түсіру

 

а) Квадрат теңдеудің түбірін қалай табамыз?

ә) Дискриминант, түбір формуласы қалай жазылады?

б) Квадрат теңсіздік анықтамасы қалай айтылады?

в) Квадрат теңсіздікті шешудің қандай әдісін білесің?

г) Парабола төбесінің формуласы қандай?

 

2.      Сан аралықтарын сәйкестендіру

 

                                                     

D [ -1;4)

C ( -1;4]

В [ -1;4]

      

 

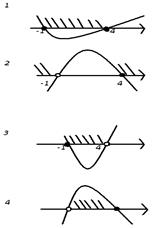
5.(-∞;5)                                                                      сәуле

6.                                                                   кесінді

7.                                                                    интервал

8.                                                                  жартылай интервал

9.                                                                   ашық сәуле

 

ІІІ.    Зерде  журналының   тапсырмасы(шексіз мейірімділік)

1. -2;0;1 сандарының қайсысы квадраттық теңсіздіктердің шешімі болады:

    а) х² +6х +8<0;       ә) х² +х>0;       б) 3х² – х +2 > 0

 

2. . Теңсіздікті қанағаттандыратын бүтін сандарды тап.

-1≤х≤3                                         3<х<6

 

3. Теңсіздіктерді шеш:

                    (х-1)(х-3) >0

 

 

ІV.Математика және физика журналының   тапсырмасы(келешекке ақ жол)

 

1. Теңсіздіктерді шеш:

    а) х² – 49 >0                                ә)   2х² – 4х +1 >0

 

2. . х-тің қандай мәндерінде өрнектің мағынасы бар болады:

 

   ;

  

V.Логика журналының   тапсырмасы( асқақ құдірет иесі)

Автобус 8 рейісте 185 –тен  көп жолаушы тасыған , ал 15  рейісте  370-тен аз жолаушы тасыған . Әрбір рейісте автобуста неше орын болса ,сонша жолаушы тасыған. Автобуста неше орын болған?

 

VІ. «МАБ» орталығының тапсырмасы( адам сәулетшісі-)

1.Өрнектің мәнін тап  :                                   А.81    В.72   С.32 Д.36  Е.144

2.Үшмүшені көбейткіштерге жікте: х+х-12  А.(х-2)(х+6)    В.(х+2)(х-6)   С.(х-3)(х-4)            Д. (х+3)(х-4)     Е. .(х-3)(х+4)  

3.Жарысқа 600 оқушы қатысты.Олардың 55%-ы –қыздар.Қанша ұл бала қатысты?

 

                                                                                                А.270   В.260   С.250 Д.240  Е.230

4. Өрнектің мәнін тап : . а=-2 b=-3 c=-4   А.1   В.-2   С.2 Д.-3  Е.3

5:Жақшаны аш:(2-3n)( 2+3n)     А.4+9n  В.4-9n С.4-3n Д.4+3 n Е. 3n -4                 

 

VІІ.Үйге тапсырма  :  №286, 290

VІІІ. Бағалау