Числовые и функциональные ряды

Числовые и функциональные ряды.

Числовые ряды: основные понятия.

Определение. Выражение вида 



u₁  u₂ u₃ L u_n L  u_n (1), где u_n R называется числовым рядом (или

n1

просто рядом).

Числа u₁, u₂, …, u_n – члены ряда (зависят от индекса n).

u_n – общий член ряда, задается как u_n = f(n). Ряд задан, если известен его общий член.

1       1 1          ^ 1       1

             Примеры. 1. 1          L       L   - гармонический ряд. u_n        .

2       3 n          n1 n     n

2. Бесконечно убывающая геометрическая прогрессия



a  aq  aq² L aq^n1 L  aq^n1 , u_n  aq^n1, q 1.

n1

Сумма первых n членов ряда (1) называется n-ной частичной суммой ряда и обозначается через S_n, т. е. S_n  u₁  u₂  u₃ L u_n .

Так S1  u1, S2  u1  u2 , S3  u1  u2  u3 и т. д.

Определение. Если существует конечный предел S  lim S_n последовательности

n

частичных сумма ряда (1) то этот предел называют суммой ряда и говорят, что ряд сходится. 



Обозначение: S_n ^ u_n .

n1

Если lim S_n не существует или  lim S_n  , то ряд (1) называют расходящимся. 

                           n                                                        n

Примеры.

                                                                    ^         1            1         1                   1

              1. Найдем сумму ряда                             L               L

                                                  n_1nn 1 12    2 3      nn 1

              1             1               1         1            1    1    1          1

S₁  1 , S₂    1       1  12 2 12 2 3  2  2 3  3

               1         1                   1              1    1    1           1       1                  1

S_n                   L               1           L              1         

            12    2 3         nn 1      2    2   3            n   n 1          n 1

                         1   

S  lim1    1 n        n 1

Ряд сходится.

2. Найдем сумму для бесконечно убывающей геометрической  прогрессии.



a  aq  aq² L aq^n1 L  aq^n1 при q 1.

n1

a1qⁿ

Для геометрической прогрессии сумма первых n членов равна S_n                 

1q

S  lim 1q         nlim1q 1q   1q  nlim1q  n

a

                 Так как qⁿ  0 , при n → ∞, если q 1, то S              и ряд сходится.

1q

                                                                                                                          1     1            1              ^ 1

             3. Можно доказать, что гармонический ряд 1          L       L   расходится.

                                                                                                                          2     3            n            n1 n



             Определение.      Ряд        u_n1  u_n2  u_n3 L u_k   u_k  r_n        называется      n-ным

kn1

остатком ряда (или остаточным членом ряда). Он получается из ряда (1) отбрасыванием n первых его членов.

Если ряд (1) сходится, то его остаток lim r_n  0 .

n

lim r_n  limS S_n  0

              n             n

Элементарные свойства рядов.

Можно рассмотреть следующие арифметические действия с рядами.



1.  Сложение и вычитание рядов, то есть построение по двум заданным рядам u_n и

n1

                                                          

vn третьего ряда un  vn .

             n1                                        n1

                                                                                                                        

2.  Умножение ряда на число, то есть c  u_n  c u_n .

                                                                                                        n1            n1



Свойство 1. Если ряд (1) сходится и его сумма равна S, то ряд c u_n , где c –

n1

произвольное число, также сходится и его сумма равна cS.

                                                                                                                                             

Свойство 2.  Если сходится ряд u_n (1) и сходится рядv_n , а их суммы равны S₁ и S₂

                                                                                        n1                                                 n1



соответственно, то сходятся и ряды u_n  v_n , причем сумма каждого равна

n1

соответственно  S₁ ± S₂.

Необходимый признак сходимости ряда.

Нахождение n – ной частичной суммы  S_n  и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. 

Теорема 1. Если ряд (1) сходится, то его общий член u_n стремиться к нулю, т. е.

lim u_n  0 . n

Следствие. (достаточное условие расходимости ряда). Если limu_n  0 или этот

n

предел не существует, то ряд расходится.

                                                                                                                      n

             Пример. Исследовать на сходимость ряд  .

n_1 2n 1

                            n         1

lim   0 - ряд расходится. n 2n 1 2

                                                                                 ^ 1                                          1

Однако гармонический ряд n_1 n - расходится, хотя nlim _n  0 !

Так как необходимый признак не является достаточным.

Достаточные признаки сходимости положительных рядов.

Определение. Ряд (1) называют положительным, если положительны все его члены.

Теорема 2. (Признак сравнения)

                                                                                                                                        

Пусть даны два знакоположительных ряда u_n (1) и v_n (2). Если для всех n  начиная

                                                                                                                n1                   n1

с некоторого номера N выполняется неравенство u_n  v_n (3), то из сходимости ряда (2) следует сходимость ряда (1), из расходимости ряда (1) следует расходимость ряда (2).

Если для рядов выполняется равенство (3), то ряд (2) называют мажорантным по отношению к (1), а ряд (1) является минорантным по отношению к (2).

Теорема 3 (предельный признак сравнения). Пусть даны два знакоположительных

uⁿ  A (0 < A < ∞), то ряда (1) и (2). Если существует конечный, отличный от 0, предел lim

n vn

ряды (1) и (2) сходятся или расходятся одновременно.

В качестве рядов для сравнения выбирают или гармонический ряд (расходящийся) или бесконечно убывающую геометрическую прогрессию (сходящийся ряд).

                                                                                                                               1

Примеры. 1. Исследовать на сходимость ряд  _n .

 1

Для сравнения выберем ряд  _n

n_1 2

n_1 n2

(б.у. геометрическая прогрессия), который сходится.

     1         1

          , т. е. ряд – сходится. _{n            n} n 2  2

                                                                                           1

2.   Исследовать на сходимость ряд  2 .

n2

 1

Сравним этот ряд с гармоническим  .

n_1 n

                           1             1

 n            2

 Поэтому данный ряд расходится.

 

3.   Исследовать на сходимость ряд tg            .

                                                                                            n1       3n

 1

Сравним этот ряд с гармоническим  , но используем предельный признак.

n_1 n



tg

              lim      3n  

              n       1         3

n

Данный ряд расходится.

Теорема 4. (Признак Даламбера).

Пусть дан ряд (1) с положительными членами и существует конечный или бесконечный u^n1  l . Тогда ряд сходится при l < 1 и расходится при l > 1. предел lim n un

Если l = 1, то признак Даламбера не дает ответа на вопрос о сходимости или расходимости ряда.

 n2

Пример. Исследовать на сходимость ряд  n1 .

n_1 3

                                                                                    n²                   n 1²

             Запишем для этого ряда: u_n ^     _n1 , u_n1 ^         _n      

                                                                                   3                       3

n 1²

               lim un1  lim        n   lim n 12  3n1  lim n 12  3n1  1 1

               n un                         nn                     3n            n2          n       n2           3n         3

3n1 Ряд сходится.

Теорема 5.(Радикальный признак Коши.)

Пусть дан ряд (1) с положительными членами и существует конечный или бесконечный предел lim ⁿ u_n  l . Тогда ряд сходится при l < 1 и расходится при l > 1.

n

Если l = 1, то признак Коши не дает ответа на вопрос о сходимости или расходимости ряда.

n

^  n 1 

Пример. Исследовать на сходимость ряд   . n_18n 1

n

                          n 1               n 1      1

lim ⁿ               lim            1 n 8n 1  n 8n 1         8

Ряд сходится.

Теорема 6. (Интегральный признак Коши).

Пусть члены ряда (1) монотонно убывают и функция y = f(x) непрерывная на x  ≥ a ≥ 1,



такова, что f(n) = u_n. Тогда ряд (1) и интеграл f xdx одновременно сходятся и расходятся.

a

                                                                                                                    ^         2n

Пример. 1. Исследовать на сходимость ряд ^ 2 2 . n1 n 1 Составляем функцию f x  ^2x 2 .

 2       x 1

b  b b 2

                    2xdx                  2xdx                    dx                        1                        1       1     1

^1 x2 1₂  blim1^ x2 1₂  blim^1 x2 1₂  blim _{x2 1}_1  blim_ _{b2 1}  ₂ _  ₂

Так как интеграл сходится, то сходится и соответствующий ряд.

 1

2. Исследуем на сходимость ряд  _p , где p > 0 – действительное число.

n_1 n

Это ряд Дирихле. Ему соответствует функция fx  ¹_p .  x

При p ≠ 1

 dx                                   b         1p b        1p           1      , если p 1 x  b      1          

p

         ^ x_p blim^1 x dx  blim1  ^p 1  blim_1  p 1  p _  __p_,_если1    _{p 1}   

1

При p = 1



dxb

 ^ _x blimlnx 1  blimlnb  ln1 

1

Мы убедились, что гармонический ряд расходится.

Таким образом указанный ряд сходится при p > 1, и расходится при p ≤ 1.

Ряды Дирихле являются очень удобным инструментом для сравнения. 

                                                                                                                        1

                Пример. Исследовать на сходимость ряд  4              .

n1 n  2

 1

Сравниваем данный ряд с рядом Дирихле  ₂ , который сходится.

n_1 n

                                       1             1         1

Так как , ряд сходится. 4

n

Знакопеременные и знакочередующиеся ряды.

Определение. Ряд (1) члены которого u_n начиная с некоторого номера n > N имеют разные знаки, называется знакопеременным.



Если ряд  u₁  u₂  u₃ L u_n L   u_n (3), составленный из абсолютных величин

n1

ряда (1) сходится, то ряд (1) также сходится и называется абсолютно сходящимся.

Если ряд (1) сходится, а (3) – расходится то ряд (1) называют условно (неабсолютно) сходящимся.

При исследовании ряда на абсолютную сходимость используют признаки сходимости рядов с положительными членами.

^ sinn

                 Пример. Исследовать на сходимость ряд  ₂           .

                                                                                                             n_1      n

^ sinn ^ sinn

             Составим ряд из абсолютных величин:      ₂            ₂       .

                                                                                                       n_1      n         n_1      n

1

sinn 1         ₂                     ₂ n   n

 1

 ₂ - сходящийся ряд Дирихле. n_1 n

Согласно признаку сравнения ряд сходится абсолютно.

Определение. Ряд вида u₁ u₂ u₃ L1^n1u_n L, где u_n > 0 (4), т. е. ряд  у которого u_n u_n1  0 называется знакочередующимся рядом.

Теорема. (признак Лейбница). Знакочередующийся ряд (4) сходится, если 

1.      Последовательность абсолютных величин членов ряда монотонно убывает,                           т.е. u₁ >  u₂  > u₃  > …> u_n > …;

2.      Общий член ряда стремится к нулю: lim u_n  0 .

n

При этом сумма S ряда (4) удовлетворяет неравенствам 0 < S < u₁.

Следствие. Остаток r_n ряда (4) всегда удовлетворяет условию: | r_n| < u_n+1. Ряды, для которых выполняются условия теоремы Лейбница называются лейбницевскими или рядами Лейбница.

                                                                                                                           ^n1 1

           Пример. Исследовать на сходимость ряд 1   .

                                                                                                             n_1                   n

Это знакочередующийся ряд, для которого выполнены условия признака Лейбница.

Следовательно ряд сходится. Однако ряд, составленный из модулей членов данного ряда это

1       1          1          ^ 1

гармонический ряд 1          L  L    , который расходится. Поэтому данный ряд

2       3          n          n1 n

сходится условно.

Теорема. Если ряд абсолютно сходится, то при любой перестановке его членов сходимость полученного ряда не нарушается и его сумма остается прежней.

Теорема. Если числовой ряд сходится условно, то задав любое число a, можно так переставить члены ряда, что его сумма окажется равной a. Более того, можно так переставить члены условно сходящегося ряда, что ряд полученный после перестановки, будет расходящимся.

Пример. Пусть сумма ряда 1 1  1 L 1^{n1 1} L равна S.

                                                                                     2     3                        n

Переставим его члены так, чтобы за одним положительным членом следовало 2 отрицательных: 

1  L 

  L 

1      1          1          1          1          1                    1

                1                     L  S

2      2          3          4          5          6                    2

Таким образом сумма ряда уменьшилась вдвое!

                                                                                                              ^              n1 2n 1

        Пример. Исследовать на сходимость ряд n_11  nn 1.

2n 1

lim 0 Ряд сходится по признаку Лейбница. ^n nn 1

^ 1n 1  2n 1  ^ 2n 1 n1                n _{n 1}      n1 _n_{n 1}

Используем интегральный признак

           ^ 2x 1dx      ^b 2x 1dx       ^b dx² 1^      2^b                 2        

 xx 1  blim1 x2  x                               blim1 x2  x      blim lnx  x 1  blim ln b  b ln2  

1

Ряд не сходится абсолютно, т.е. сходится условно.

Всякая n - ная  частичная сумма сходящегося ряда является приближением к его сумме с точностью не превосходящей абсолютной величины остатка ряда δ ≤ | r_n|.

                                                                                                                   2                       3                                n

1       1 1          1 1             1 1 

             Пример. Вычислить сумму ряда                     L         с точностью     

2       2!  2       3!  2           n! 2 

δ = 0,001.

Нужно оценить какое количество членов ряда надо суммировать, чтобы остаток ряда    

| r_n| ≤ δ.

n1       n2 1     1    1          1 

              r_n                                        L

                    n 1! 2   n  2!  2 

  Так как n 1! n  2! n  3! L_→     ¹      _      ¹      _         ¹   L

                                                                                                    n 1! n  2! n 3!

1  1 n^1  1  1 ²  1  1 ^n1 r_n    1        

                   n 1!  2       2    2    n 1!  2 

n1

1 1 

r_n   

n 1!  2 

2

                        1 1        1

              r₁             

                      2! 2       8

3

                        1 1         1

              r₂                  0.0208

                      3!  2       48

4

                        1 1            1

              r₃                         0.0026

                      4!  2      24 16

5

1                      1  1

              r₄                           0.00026

                      5!  2      120 32

Следовательно необходимо найти сумму 4-х членов ряда для получения заданной точности.

2                      3          4

                                   1     1 1        1 1        1 1        1     1      1        1

             S  S₄                                                        0.648

                                   2    2!  2      3! 2      4!  2       2     8     48     384

Функциональные и степенные ряды.

Определение. Пусть функции u_i(x), i = 1, 2, …, n определены в области D. Тогда выражение вида 



u₁x u₂ x u₃ xL u_n xL  u_n x(5) называется функциональным рядом.

n1

Если зафиксировать точку x₀, то из ряда (5) получим числовой ряд:

u₁x₀ u₂x₀ u₃x₀L u_nx₀L

Если полученный числовой ряд сходится, то точка x₀ называется точкой сходимости ряда (5), если же ряд расходится – точкой расходимости функционального ряда.

Множество значений x, при которых ряд (5) сходится, называется областью сходимости функционального ряда.

Как правило область сходимости является частью области определения функции.

(DS  Dx )

Пример. Найти область сходимости функционального ряда



lnx  ln² x  ln³ x Llnⁿ x L  lnⁿ x

n1

Это геометрическая прогрессия с q = ln x. При |q| < 1 геометрическая прогрессия сходится.

1

                lnx 1     x  e.

e

Так как каждой точке x  D_S соответствует некоторое число – сумма числового ряда, то в области сходимости функционального ряда его сумма является некоторой функцией от x: S = S(x). 

S_nx  u₁x u₂x u₃xLu_nx - n –ная частичная сумма ряда.

Также определен остаточный член ряда  r_nx  SxS_nx  u_n1x u_n2xL

В области сходимости ряда  limS_nx  Sx и lim r_nx  0 .

              n                                      n

Равномерная сходимость функционального ряда.



Сходимость ряда u_n x на множестве D_S к функции S(x) означает, что при x  D_S

n1

S_n(x) при достаточно большом n мало отличается от S(x), т.е  0 такой номер N₀ =N₀(x), что при n > N₀ справедливо | S_n(x) - S(x)| <   или | r_n(x)| <   .

Т.е. в общем случае N₀ зависит от x. Это означает неравное количество членов ряда для каждой точки x  D_S, т.е. неравномерная сходимость.



Определение. Функциональный ряд u_n x называется равномерно сходящимся на

n1

множестве D_S к функции S(x), если  0 найдется такое N, что  n > N и 

x  D_Sсправедливо неравенство | S_n(x) - S(x)| <   .

Графическое пояснение: Равномерная сходимость означает, что графики S_n(x) начиная с номера N попадают в  - коридор графика S(x).

Определение. Функциональный ряд (5) называется мажорируемым в некоторой



области D, если существует сходящийся числовой ряд _n, _n  0, такой что 

n1

x  D_Sсправедливо | u_n(x)| ≤ α_n (n = 1, 2, …) .

Теорема. (Признак равномерной сходимости Вейерштрасса). Если для рада (5) на D существует мажорирующий (мажорантный) числовой ряд, то функциональный ряд (5) сходится на D равномерно.

                                                                                                                   cos x     cos2x     cos3x             cosnx

              Пример. Рассмотрим функциональный ряд                   ₂              ₂       L ₂  L.

                                                                                                                        1            2              3                     n

                                                                                                                                                                     cosnx       1

             Данный ряд мажорируемый на всей числовой оси Ox, так как  x         ₂           ₂ .

                                                                                                                                                                         n           n

 1

Числовой ряд  ₂ - сходится. Следовательно, рассматриваемый ряд равномерно

n_1 n

сходится на всей числовой оси.

Теоремы о равномерно сходящихся рядах.



Теорема 1. Если члены ряда u_n x - непрерывные функции и ряд на отрезке [a, b]

n1



сходится равномерно к S(x), то и Sx  u_n x является непрерывной функцией.

n1 

Теорема 2. (о почленном интегрировании). Если ряд u_n xсходится к  S(x)

n1

равномерно и каждая из функций u_i(x) (i = 1, 2, …, n) и S(x) интегрируема на отрезке [a, b],

 b    b т^о u_nxdx  Sxdx .

      n1a                         a



 Теорема 3. (о почленном дифференцировании). Пусть ряд u_n x сходится к

n1

некоторой функции S(x)  на отрезке [a, b] и каждая из функций u_i(x) (i = 1, 2, …, n)



непрерывно дифференцируема на отрезке [a, b]. Тогда если ряд u_n x, членами которого

n1

являются производные u′_i (x) от функций u_i(x), сходится равномерно, то функция S(x) 



дифференцируема и в каждой точке отрезка [a, b] справедливо равенство u_n x  Sx

n1

Среди всевозможных функциональных рядов особое значение имеют степенные и тригонометрические ряды (ряды Фурье).

Степенные ряды.

Определение. Степенным рядом называется функциональный ряд вида



a₀  a₁x  x₀  a₂ x  x₀ ² L a_n x  x₀ ⁿ L  a_n x  x₀ ⁿ (1),  

n0

где a₀, a₁, a₂, …, a_n  - постоянные числа, называемые коэффициентами ряда, а x₀ – фиксированное число.

При x₀ = 0 имеем частный случай степенного ряда:



a₀  a₁x  a₂x² L a_nxⁿ L  a_nxⁿ (2).

n0

Степенные ряды состоят из сравнительно простых функций u_n(x) = a_n(x - x₀)ⁿ  и их частичные суммы являются многочленами. Эта простота приводит к тому, что степенные ряды обладают многими свойствами, которыми другие функциональные ряды не обладают.

Теорема (Абеля). Для всякого степенного ряда существует такое неотрицательное число R, конечное или бесконечное (0 ≤ R ≤ ∞), что ряд сходится абсолютно при всех x, удовлетворяющим условию | x – x₀| < R  и расходится при всех x, удовлетворяющим условию

| x – x₀| > R . 

Если R = 0, ряд расходится везде кроме точки x = x₀. Если R = ∞, то ряд сходится на всей числовой оси.

Утверждение теоремы не относится к случаю | x – x₀| = R, здесь может быть как сходимость, так и расходимость.

 Множество точек  x, удовлетворяющих условию | x – x₀| < R , представляет собой внутренность круга с центром в x₀ на комплексной плоскости, а для действительных степенных рядов числовой интервал (x₀ – R, x₀ + R) с центром в x₀. Поэтому это множество точек называют кругом сходимости или интервалом сходимости. R  - радиус сходимости.

Свойства степенных рядов.



Теорема 1. Если степенной ряд  a_n x  x₀ ⁿ (1) имеет радиус сходимости R,  то на

n0

любом отрезке действительной оси (в  круге комплексной плоскости) вида | x – x₀| < r, r < R он сходится равномерно.

                                                                                                                                                                   aⁿ                     или lim, то

Теорема 2. Если для степенного ряда (1) существует предел lim

                                                                                                                                                         n an1                n n

этот предел равен радиусу сходимости R. 

                                                                       aⁿ            или R  lim.

Таким образом: R  lim

                                                              n an1                           n n

Данная теорема следует из признаков Даламбера и Коши для числовых рядов.

Свойство 1. На интервале сходимости (x₀ – R, x₀ + R) сумма S(x) степенного ряда является непрерывной функцией.

Свойство 2. Степенной ряд (1) можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости.

Свойство 3. Степенной ряд можно почленно дифференцировать внутри интервала сходимости.

Это все следствия из соответствующих теорем о равномерно сходящихся функциональных рядах.

 2n  xn

               Пример 1. Найти область сходимости ряда  _n              .

n_13  n

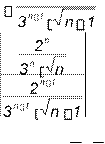2n             2n1 an    an1

                                                                                       2ⁿ 3^n1  n 1      3          n 1     3

R  lim           lim                         lim                                  lim               

           n                                        nn 2n1 3n  n                         2 n          n        2

                                                              3   3                      3

            Ряд сходится в интервале     ,     . При x      исследуем отдельно.

                                                                           2   2                      2

n

                                        2n  3     2n 1n  3n

                           3                          2          

             x                n                n         2n   1n . Данный ряд сходится по

2         n1 3       n          n1          3       n          n1           n

признаку Лейбница для знакопеременных рядов.

n

3         ^ 2n_n^ 3² ^       2_nn  ²3nn   1 . Это ряд Дирихле с  = ½ , то есть он

              x _         

2         n1 3       n          n1 3  n          n1          n

расходится.

3         3

             Область сходимости:[    ,     ).

                                                                   2    2

                                                                                                                   ^{          n} x  2ⁿ

           Пример 2. Найти область сходимости ряда 1  _n                   .

                                                                                                                 n_1             2    n 1

1n               1n1 an  n                an1     n1          

                         2    n 1               2       n  2

1ⁿ

R  lim an  lim 2n  n 1  lim 2n1  n  2  2 lim n 2  2

n an1 n 1n1 n 2n  n 1 n n 1

2n1  n  2

Так как x₀ = 2, интервал сходимости (x₀ – R, x₀ + R) = (2 – 2, 2 + 2) = (0, 4). На границах интервала в точках x = 0 и x = 4 исследуем дополнительно.

            0  2n                             n               2n                           2n                  1 n

x = 0 1^ _n  1^ _n  _n  n1 2  n 1 n1 2  n 1 n1 2  n 1 n1 n 1

Ряд расходится.

                                     ⁿ 4  2n                      n          2n                1n

x = 4 1 _n  1^ _n  Данный ряд сходится по n1 2  n 1 n1 2  n 1 n1 n 1

признаку Лейбница для знакопеременных рядов.

Область сходимости: (0, 4].

 xn

             Пример 3. Найти область сходимости ряда  .

n1 n!

1  1 an     an1  n!

aⁿ lim n!n 1  limn 1  

R  lim

                                             n ^a_n1n                              n!           n

Область сходимости: (- ∞, +∞).

Разложение функций в степенные ряды.



Пусть ряд a_n x  x₀ ⁿ сходится при | x – x₀| < r, и его суммой является функция f(x). 

n0



a_n x  x₀ ⁿ  fx.

n0

Говорят, что функция f(x) разложена в степенной ряд (1) на множестве | x – x₀| < r.

Разложение функции в степенной ряд (если это возможно) бывает полезным при решении многих математических задач.

Пусть функция f(x) определена в некоторой окрестности точки x₀ и бесконечное число раз дифференцируема в этой точке, тогда можно найти коэффициенты a_n степенного ряда по формулам:

a_n  _f nx0  и для функции построить бесконечный ряд n!

fx ^  a_n  f nx0x  x0n x  x0n 

n0              n0 n! называемый рядом Тейлора функции f(x) в точке x₀.

Частный случай ряда Тейлора при x₀ = 0 – ряд Маклорена.

x   a_nxⁿ   _f n^0x_n

f

                            n0                 n0      n!

Необходимое условие разложимости функции в степенной ряд это дифференцируемость бесконечное число раз. Но это не достаточное условие! Так как вовсе не следует, что ряд будет сходиться к данной функции f(x); он может оказаться расходящимся или сходиться, но не к функции f(x).

  12

Пример. Рассмотрим функцию f x  ^e ^x , x  0 . x0  0

                                                                                                   _   0, x  0

Функция бесконечное число раз дифференцируема в точке x₀ = 0. 0  f 0  f 0  f0  L  f ^n0 и степенной ряд Маклорена:

f0  f0 ^f⁰x  ^f⁰ x² L ^{f n}⁰ xⁿ L  0  0  x  0  x² L0  xⁿ L  0

                                            1!            2!                      n!

Этот ряд сходится в любой точке, но его сумма S(x) = 0 а не f(x).

Т.е. необходимо условие при котором ряд Тейлора, построенный по бесконечно дифференцируемой в точке x₀ функции f(x), совпадает с ней на всем интервале сходимости.

Необходимое условие разложимости функции в ряд Тейлора.

Пусть f(x) – заданная бесконечно дифференцируемая функция и ее ряд Тейлора

fx  fx₀ ^f^x0x  x₀ ^f^x0x  x₀² L ^{f n}^x0x  x₀ⁿ LR_nx, где R_n(x) –

                                                1!                        2!                                  n!

остаточный член данного ряда. Коротко можно записать  f x P_nx R_nx, где 

P x fx  fx0x  x  fx0x  x 2 L f nx0x  x n - многочлен

                 n                   0                                  0                                   0                                                  0

                                                   1!                        2!                                  n!

Тейлора. (n- ная частичная сумма ряда Тейлора S_n(x))

Теорема. Для того чтобы бесконечно дифференцируемая в точке x₀ функция f(x) являлась суммой составленного для нее ряда Тейлора, необходимо и достаточно, чтобы в каждой точке x его интервала сходимости выполнялось равенство  lim R_nx  0 . n

Данная теорема показывает, что вопрос о разложимости функции в ряд Тейлора сводится к исследованию поведения остатков Тейлора функции f(x) при n→∞, а именно если

lim R_nx₀  0 , то ряд Тейлора в точке сходится и f(x₀) является суммой ряда при x = x₀, если n

это не выполняется или предел не существует, то в точке x = x₀ ряд Тейлора или не сходится или его сумма не совпадает с f(x₀). Поэтому для решения вопроса требуется найти форму остатка Тейлора функции f(x).

Можно доказать, что остаточный член может быть представлен в виде:

                           f n1c       n1

          R_nx ^ x  x₀ , c x₀, x - остаточный член в форме Лагранжа.

n 1!

Теорема. (простой достаточный критерий разложимости функции в ряд Тейлора).

Пусть f(x) задана на (a, b) и имеет проиозводные всех порядков. Если число М такое, что  n  N  и  x [a, b] оказывается | f⁽ⁿ⁾(x)| ≤ M, то функция раскладывается в ряд Тейлора на [a, b].

Доказательство.

Необходимо доказать, что lim R_nx  0 .

n

lim R_nx  lim ^f n1cx  x₀n1 lim M  x  x0n1  M  lim x  x0n1 n            n n 1!n             n 1!        n n 1!

Осталось показать, что 

lim x  x0n1 _{ 0} ^n n 1!

 x  ^x₀n1

            Рассмотрим ряд  n 1!   

n0

lim

                       u^n1  lim n  2n!1  nlim n  2!                                 n 1!     x  x₀nlim n12  0 1

               n ^u_n          n x  ^x₀

n 1!

По признаку Даламбера этот ряд сходится на всей числовой оси. Тогда в силу необходимого признака сходимости

lim u_n  lim 0 n         n^          n 1!

То есть lim R_nx  0 и теорема доказана.

n

 Разложение некоторых элементарных функций в ряд Тейлора (Маклорена).

Для разложения функции f(x) в ряд Маклорена нужно:

1.      Найти производные fx, fx,L,f ^nx.

2.      Вычислить значения производных в точке x₀ = 0.

3.      Записать ряд для заданной функции и найти его интервал сходимости.

4.      Найти интервал (-R, R), в котором остаточный член ряда R_n(x) → 0 при n→∞.

Разложение функции e^x. fx  fx  L  f ^nx  e^x

Для ряда Маклорена при x₀ = 0: f0  f 0  L  f ^n0  e⁰ 1

1

a_n   n!

Составляем ряд Маклорена для функции e^x:

fx 1 ¹ x  ¹ x² L ¹ xⁿ L 1 ^x  ^x2 L ^xn L

                                   1!       2!                 n!                      1!     2!             n!

Найдем радиус сходимости. (уже находили такой радиус).

                                  aⁿ       lim lim n!n 1  limn 1  

R  lim

                        n ^a_n1                      nn                       n!           n

То есть ряд сходится в интервале (- ∞, +∞). Выпишем остаток ряда и покажем, что lim R_nx  0 .

n

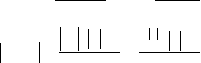x  ^f n1cxn1  ec xn1 c 0, x R_n n 1! n 1! ec  x n1 e x  x n1

           R_nx                                 

                                n 1!    n 1!

При фиксированном x R_n(x) → 0 при n→∞.

                                             2                   n

e^x 1 ^x  ^x L ^x L 

                                1!     2!             n!

Разложение функции sin(x). fx  cos x    f0 1 fx  sinx  f0  0 fx  cos x  f0  1

f ^4x  sinx f ^4x  0 f ^5x  cos x f ^5x 1