Cпособы решения банковских задач при подготовке к ЕГЭ.

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Cпособы решения банковских задач при подготовке к ЕГЭ

 

Исследовательская работа

 

 

 

 

 

 

 

 

                                                                Выполнила: И.В. Лужных,
                                                                 учитель математики МБОУ «СОШ № 2»,

                      г. Ленинск-Кузнецкий

 

______________

                                                                              (подпись)

 

 

Ленинск-Кузнецкий

2021

 

Оглавление

Введение…………………………………………………………………………..3

1.     Обоснование выбора описываемого в данной работе решения ……….4

2.     Основные виды банковских заданий ……………..……………………..5

2.1.          Банковские задачи направленные на уменьшение суммы основного долга на одну и ту же сумму ………………………………………….5

2.2.          Банковские задачи направленные на уменьшение суммы основного долга, когда сумма выплат одинаковая или разная …………………9

2.3.          Банковские задачи, направленные на вклад ……………………...…12

Заключение……………………………………………………………………….15

Литература……………………………………………………………………….16

Приложения………………………………………………………………….......17

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Во второй части ЕГЭ может присутствовать банковская задача, которую решить по силам даже десятикласснику, если изучить удобный и доступный способ решения. Методы решения задач данного типа, представленные в сети Интернет часто не являются универсальными, простыми, достаточно обоснованными. Поэтому необходимы способы, которые отвечали бы данным критериям.

Таким образом, изучение этих способов является актуальным уже в 10 классе.

Объект исследования: банковские задачи на ЕГЭ.

 Предмет исследования: основные типы банковских задач и способы их решения.

Гипотеза – существуют простые и удобные методы решения банковских задач, представленных в ЕГЭ, овладеть которыми могут учащиеся десятых классов общеобразовательных школ.

Цель: изучение наиболее рационального способа решения банковских задач

Задачи:

1.Рассмотреть типы банковских заданий на ЕГЭ и изучить их возможные способы решения.

2.Выбрать наиболее рациональный способ.

3.Применить способ для решения разных типов заданий

4.Создать сборник задач по данной теме.

Практическая значимость работы – составление задачника с распределением задач по способам решения.

 

 

 

 

Обоснование выбора описываемого в данной работе решения.

При выборе метода по решению банковских заданий мной предъявлялись следующие требования:

-полнота, обоснованность;

-простота применения;

-наглядность;

-универсальность;

-доступность для решения задачи десятыми классами.

Больше всего этим критериям соответствует решение с помощью таблиц. Также в решении удобно применять коэффициент, на который умножается основная сумма долга или вклада, b = 1 +  , где r - месячная или годовая ставка.[2]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.Основные виды банковских заданий и способы их решения.

2.1. Банковские задачи направленные на уменьшение суммы основного долга на одну и ту же сумму.

Для решения данного типа задач можно воспользоваться следующим алгоритмом.

1.     Обозначаем основную сумму долга за n×S, где n – количество месяцев или лет, месячную процентную ставку, коэффициент умножения суммы долга.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в третьей - сумма долга с процентами, в следующих – сумма платежа и сумма оставшегося долга.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию.

Примеры.

Рисунок 1.Задание 1[1]

Решение.

Пусть 6S – сумма, взятая Антоном в кредит

r % - месячная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

 

Месяц	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	6S	6Sb	6Sb-5S	5S
2	5S	5Sb	5Sb -4S	4S
3	4S	4Sb	4Sb - 3S	3S
4	3S	3Sb	3Sb - 2S	2S
5	2S	2Sb	2Sb - S	S
6	S	Sb	Sb	0

Сумма всех выплат равна 21Sb – 15 S

Обозначим изначальную сумму долга за 100 процентов, а сумму всех выплат за 163 процента, тогда

6S – 100%

21Sb - 15S   ̶  163%

Решая пропорцию, получаем:

2100Sb – 1500S = 978 S

2100b = 2478

b =  = 1,18

Так как b = 1 +  ,

Откуда r = 18%

Ответ: 18%.

Рисунок 2. Задание 2 [4]

Решение.

Пусть 24S – сумма, взятая Жанной в кредит

r % - месячная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,02

Месяц	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	24S	24Sb	24Sb - 23S	23S
2	23S	23Sb	23Sb - 22S	22S
3	22S	22Sb	22Sb - 21S	21S
4	21S	21Sb	21Sb - 20S	20S
5	20S	20Sb	20Sb -19S	19S
6	19S	19Sb	19Sb - 18S	18S
7	18S	18Sb	18Sb - 17S	17S
8	17S	17Sb	17Sb -16S	16S
9	16S	16Sb	16Sb -15S	15S
10	15S	15Sb	15Sb -14S	14S
11	14S	14Sb	14Sb - 13S	13S
12	13S	13Sb	13Sb - 12S	12S
13	12S	12Sb	12Sb - 11s	11S
14	11S	11Sb	11Sb - 10S	10S
15	10S	10Sb	10Sb - 9S	9S
16	9S	9Sb	9Sb - 8S	8S
17	8S	8Sb	8Sb - 7S	7S
18	7S	7Sb	7Sb -6S	6S
19	6S	6Sb	6Sb - 5S	5S
20	5S	5Sb	5Sb - 4S	4S
21	4S	4Sb	4Sb - 3S	3S
22	3S	3Sb	3Sb - 2S	2S
23	2S	2Sb	2Sb -s	S
24	S	Sb	Sb	0

Сумма всех выплат за первый год кредитования равна

37Sb*6 – 35S*6 = 222Sb –210S= 222*0,05*1,02 – 210*0,05= 0,822 млн рублей=

= 822000 руб.

Ответ: 822000 руб.

 

 

 

2.2 Банковские задачи направленные на уменьшение суммы основного долга, когда сумма выплат одинаковая или разная

        Для решения данного типа задач воспользуемся следующим алгоритмом.

1.     Обозначим сумму, взятую в кредит за S, месячную процентную ставку, коэффициент умножения суммы долга, платеж.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в третьей- сумма долга с процентами, в следующих – сумма платежа и сумма оставшегося долга.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию.

Примеры.

Рисунок 3. Задание 3[3]

Решение.

Пусть S руб. – сумма, взятая в кредит

r = 10% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,1

x руб. – сумма платежа в первый год

2x руб. – сумма платежа во второй год

3x руб. – сумма платежа в третий год

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	S	Sb	x	Sb -x
2	Sb -x	Sb² - bx	2x	Sb² -bx - 2x
3	Sb² -bx - 2x	Sb³ -b²x - 2bx	3x	Sb³ -b²x - 2bx - 3x = 0

 

 

x +2x + 3x =2395800

x = 399300

Так как долг погашен,

Sb³ -b²x - 2bx - 3x = 0

Sb³ = b²x + 2bx+ 3x

Sb³ = x(b² + 2b+ 3)

S =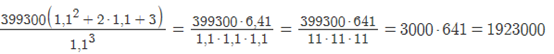руб.

 

 Ответ: 1923000 руб.

 

 

Рисунок 4. Задание 4[3]

Решение.

Пусть S руб. – сумма, взятая в кредит

r = 31% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,31

x = 69690821 руб. – сумма ежегодного платежа

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	S	Sb	x	Sb - x
2	Sb - x	Sb² - bx	x	Sb² - bx - x
3	Sb² - bx - x	Sb³ - b²x - bx	x	Sb ³- b²x-bx–x=0

 

Так как долг погашен,

 Sb³ - b²x - bx – x = 0

Sb³ - b²x - bx - x = 0

Sb³ = b²x + bx+ x

Sb³ = x(b² + b+ 1)

S = 124809100 рублей

 Ответ: 124809100 руб.

 

 

 

 

 

 

 

 

 

 

 

 

2.3. Банковские задачи, направленные на вклад.

        Для решения данного типа задач воспользуемся следующим алгоритмом.

1.     Обозначим сумму вклада за S, месячную процентную ставку, коэффициент умножения суммы долга, платеж.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма вклада, в третьей - сумма вклада с процентами, в следующих (если необходимо) - сумма платежа и сумма остатка.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию

Примеры.

Рисунок 5. Задание 5[1]

Решение.

Пусть S руб. – изначальная сумма вклада

r = 10% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма вклада

b = 1,1

x = 2000 руб.– сумма, которая снимается со вклада

Для запланированной суммы

Год	Вклад	Вклад с процентами
1	S	Sb
2	Sb	Sb²
3	Sb²	Sb³

 

 

 

Для фактической суммы

Год	Вклад	Вклад с процентами	Остаток
1	S	Sb	Sb - x
2	Sb - x	Sb² - bx	Sb² - bx +x
3	Sb² - bx +x	Sb³ - b²x +bx

 

Разница между запланированной и фактической суммой равна

Sb³ - (Sb³ - b²x +bx) = b²x - bx = 1,1²×2000 – 1,1×2000= 220 руб.

То есть, вкладчик получит на 220 руб. меньше запланированной суммы
Ответ: 220 руб.

Рисунок 6. Задание 6[5]

Решение.

Пусть S = 400000 руб. – изначальная сумма вклада

r = 12,5% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма вклада

b = 1,125

m – сумма, на которую пополняется вклад

Год	Основная сумма вклада	Платеж	Сумма вклада с процентами
1	S	-	Sb
2	Sb	-	Sb²
3	Sb²	m	Sb³+mb
4	Sb³+mb	m	Sb⁴+mb²+mb

 

Так как сумма на вкладе к четвертому году должна быть не меньше должна быть не меньше 7000000 руб.,

Sb⁴+mb²+mb >700000

m(b²+b)>700000 - Sb⁴

m >

m > 24795,751633…руб.

Так как m – целое число, m минимальное равно 25 тысяч рублей
Ответ: 25 тысяч руб.

Заключение

Был выбран наиболее рациональный и соответствующий критериям способ решения банковских задач. Этот метод был успешно применен для решения задач из разных сборников для подготовки к ЕГЭ. Была доказана его простота, доступность для учащихся десятых классов.

Для успешной подготовки учащихся к ЕГЭ был составлен задачник, помогающий в изучении данного способа решения банковских задач, который разбит на главы по типам заданий и содержит как задания с готовым решением, так и задачи для самостоятельного решения с ответами для самопроверки.

Данный задачник был предложен ученикам десятого класса школы №2 в качестве вспомогательного пособия для подготовки к ЕГЭ.

Работая над темой данной работы, можно сделать вывод, что несмотря на кажущуюся сложность и многообразие банковских задач на ЕГЭ, начинать готовиться к их успешному выполнению можно уже в десятом классе общеобразовательных школ, что становиться возможным, используя предложенный в данной работе способ.

 

Литература.

1.     Математика. Подготовка к ЕГЭ 2020. Профильный уровень. 40 тренировочных вариантов по демоверсии 2020 года : учебно-методическое пособие / под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион, 2019. – 416с. – (ЕГЭ)

2.     Алгебра : 9 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М. : Вентана-Граф, 2018. – 304 с. : ил.

3.     ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под редакцией И.В. Ященко. – М. :  Издательство «Национальное образование», 2019. – 256с. – (ЕГЭ. ФКР – школе)

4.     Решу ЕГЭ Дмитрий Гущин.

 https://math-ege.sdamgia.ru/test?theme=221

5.     ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под редакцией И.В. Ященко. – М. :  Издательство «Национальное образование», 2020. – 256с. – (ЕГЭ. ФКР – школе)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложения.

Задачник

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2»

НОУ «Эрудит»

 

 

 

 

Cпособы решения банковских задач при подготовке к ЕГЭ

 

Задачник с рекомендациями

 

 

 

 

 

 

 

 

 

 

 

Ленинск-Кузнецкий

2021

Содержание

 

Введение………………………………………………………………………..….3

§1. Банковские задачи направленные на уменьшение суммы основного долга на одну и ту же сумму ………………………………………………..…………..4

§2. Банковские задачи направленные на уменьшение суммы основного долга, когда сумма выплат одинаковая или разная …………………………..……….10

§3. Банковские задачи, направленные на вклад …………………….……..…..16

Ответы………………………………………………………………………...….19

Литература………………………………………………………………….……20

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Данное пособие предназначено для подготовки к ЕГЭ по математике профильного уровня. Банковские задачи относятся к заданиям, готовиться к которым можно с успехом уже в десятом классе. Существует много методов решения задач этого типа, но в этом задачнике рассмотрен рациональный способ, отвечающий всем критериям к решению. В данном задачнике представлены основные способы решения, проработанные примеры и задания для самостоятельного решения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§1. Банковские задачи направленные на уменьшение суммы основного долга на одну и ту же сумму.

Для решения данного типа задач можно воспользоваться следующим алгоритмом.

1.     Обозначаем основную сумму долга за n×S, где n – количество месяцев или лет, месячную процентную ставку, коэффициент умножения суммы долга.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в третьей- сумма долга с процентами, в следующих – сумма платежа и сумма оставшегося долга.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию.

Примеры.

Решение.

Пусть 6S – сумма, взятая Антоном в кредит

r % - месячная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

 

 

 

 

Месяц	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	6S	6Sb	6Sb-5S	5S
2	5S	5Sb	5Sb -4S	4S
3	4S	4Sb	4Sb - 3S	3S
4	3S	3Sb	3Sb - 2S	2S
5	2S	2Sb	2Sb - S	S
6	S	Sb	Sb	0

Сумма всех выплат равна 21Sb – 15 S

Обозначим изначальную сумму долга за 100 процентов, а сумму всех выплат за 163 процента, тогда

6S – 100%

21Sb - 15S   ̶  163%

Решая пропорцию, получаем:

2100Sb – 1500S = 978 S

2100b = 2478

b =  = 1,18

Так как b = 1 +  ,

Откуда r  = 18%

Ответ: 18%.

 

 

 

 

 

Решение.

Пусть 24S – сумма, взятая Жанной в кредит

r % - месячная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,02

Месяц	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	24S	24Sb	24Sb - 23S	23S
2	23S	23Sb	23Sb - 22S	22S
3	22S	22Sb	22Sb - 21S	21S
4	21S	21Sb	21Sb - 20S	20S
5	20S	20Sb	20Sb -19S	19S
6	19S	19Sb	19Sb - 18S	18S
7	18S	18Sb	18Sb - 17S	17S
8	17S	17Sb	17Sb -16S	16S
9	16S	16Sb	16Sb -15S	15S
10	15S	15Sb	15Sb -14S	14S
11	14S	14Sb	14Sb - 13S	13S
12	13S	13Sb	13Sb - 12S	12S
13	12S	12Sb	12Sb - 11s	11S
14	11S	11Sb	11Sb - 10S	10S
15	10S	10Sb	10Sb - 9S	9S
16	9S	9Sb	9Sb - 8S	8S
17	8S	8Sb	8Sb - 7S	7S
18	7S	7Sb	7Sb -6S	6S
19	6S	6Sb	6Sb - 5S	5S
20	5S	5Sb	5Sb - 4S	4S
21	4S	4Sb	4Sb - 3S	3S
22	3S	3Sb	3Sb - 2S	2S
23	2S	2Sb	2Sb -s	S
24	S	Sb	Sb	0

Сумма всех выплат за первый год кредитования равна

37Sb*6 – 35S*6 = 222Sb –210S= 222*0,05*1,02 – 210*0,05= 0,822 млн рублей=

= 822000 руб.

Ответ: 822000 руб.

 

Решение.

Пусть 9S – сумма, взятая Антоном в кредит

r  = 12% - месячная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,12

Месяц	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	9S	9Sb	9Sb - 8S	8S
2	8S	8Sb	8Sb - 7S	7S
3	7S	7Sb	7Sb -6S	6S
4	6S	6Sb	6Sb - 5S	5S
5	5S	5Sb	5Sb - 4S	4S
6	4S	4Sb	4Sb - 3S	3S
7	3S	3Sb	3Sb - 2S	2S
8	2S	2Sb	2Sb -s	S
9	1S	1Sb	Sb	0

 

Сумма всех выплат равна

10Sb *4 + 5Sb – 9S*4= 45Sb – 36S

Пусть сумма всех выплат – z%, а изначальная сумма кредита – 100%

45Sb – 36S  -z%

9S - 100%

4500Sb – 3600S = 9 Sz

9z = 1440

z = 160% cумма, выплаченная банку

160% - 100% = 60%  составляет плата сверх кредита

Ответ: 60%.

Задания для самостоятельного решения

1.     1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей?

2.     31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

3.     31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§2. Банковские задачи направленные на уменьшение суммы основного долга, когда сумма выплат одинаковая или разная

Для решения данного типа задач воспользуемся следующим алгоритмом.

1.     Обозначим сумму, взятую в кредит за S, месячную процентную ставку, коэффициент умножения суммы долга, платеж.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма долга, в третьей- сумма долга с процентами, в следующих – сумма платежа и сумма оставшегося долга.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию.

Примеры.

Решение.

Пусть S руб. – сумма, взятая в кредит

r  = 10% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,1

x руб. – сумма платежа в первый год

2x руб. – сумма платежа во второй год

3x руб. – сумма платежа в третий год

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	S	Sb	x	Sb -x
2	Sb -x	Sb² - bx	2x	Sb² -bx - 2x
3	Sb² -bx - 2x	Sb³ -b²x - 2bx	3x	Sb³ -b²x - 2bx - 3x = 0

 

 

x +2x + 3x =2395800

x = 399300

Так как долг погашен,

Sb³ -b²x - 2bx - 3x = 0

Sb³ =  b²x + 2bx+ 3x

Sb³ =  x(b² + 2b+ 3)

S =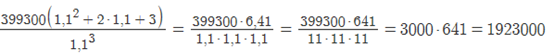руб.

 

 Ответ: 1923000 руб.

 

 

Решение.

Пусть S руб. – сумма, взятая в кредит

r  = 31% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,31

x = 69690821 руб. – сумма ежегодного платежа

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	S	Sb	x	Sb -x
2	Sb -x	Sb² - bx	x	Sb² -bx - x
3	Sb² -bx - x	Sb³ -b²x - bx	x	Sb³ -b²x-bx–x=0

 

Так как долг погашен,

 Sb³ -b²x - bx – x = 0

Sb³ -b²x - bx - x = 0

Sb³ =  b²x + bx+ x

Sb³ =  x(b² + b+ 1)

S = 124809100 рублей

 Ответ: 124809100 руб.

Решение.

Пусть S = 2180000 руб. – сумма, взятая в кредит

r  = 40% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,4

x руб. – сумма ежегодного платежа

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа	Сумма оставшегося долга
1	S	Sb	x	Sb -x
2	Sb -x	Sb² - bx	x	Sb² -bx - x
3	Sb² -bx - x	Sb³ -b²x - bx	x	Sb³ -b²x-bx–x=0

Так как долг погашен,

 Sb³ -b²x - bx – x = 0

Sb³ -b²x - bx - x = 0

Sb³ =  b²x + bx+ x

Sb³ =  x(b² + b+ 1)

x = 1372000 руб.

Сумма всех выплат равна 3x

Сумма переплат равна 3x – S = 1 936 000 руб.

Ответ: 124809100 руб.

Решение.

Пусть S руб. – сумма, взятая в кредит

r  = 5% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма долга

b = 1,05

Год	Основная сумма долга	Сумма долга с процентами	Сумма платежа
1	S	Sb	Sb - 0,9S
2	0,9S	9Sb	0,9Sb - 0,8S
3	0,7S	8Sb	0,8Sb - 0,7S
4	0,8S	7Sb	0,7Sb -0,6S
5	0,6S	6Sb	0,6Sb - 0,5S
6	0,5S	5Sb	0,5Sb

 

Сумма всех выплат равна

4,5Sb – 3,5 S = 1, 225S

1, 225S – z%

S – 100%

z =

z = 122,5%

Сумма выплат сверх суммы основного кредита равна

122,5% - 100% = 22, 5%

Ответ: 22,5 %.

 

Задания для самостоятельного решения

1.     Фермер получил кредит в банке под определенный процент годовых. Через год фермер в счет погашения кредита вернул в банк  от всей суммы, которую он должен банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму, на 21% превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

2.     15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

3. В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:

— каждый январь долг возрастает на r% по сравнению с концом предыдущего года.

— с февраля по июнь необходимо выплатить часть долга.

— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.

— суммы выплат 2020 и 2021 годов равны.

Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Банковские задачи, направленные на вклад.

        Для решения данного типа задач воспользуемся следующим алгоритмом.

1.     Обозначим сумму вклада за S, месячную процентную ставку, коэффициент умножения суммы долга, платеж.

2.     Строим таблицу, в первой колонке – месяц или год, во второй – основная сумма вклада, в третьей- сумма вклада с процентами, в следующих (если необходимо) - сумма платежа и сумма остатка.

3.     Пользуемся таблицей и находим нужные величины, решая уравнение или составляя пропорцию

Примеры.

Решение.

Пусть S руб. – изначальная сумма вклада

r  = 10% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма вклада

b = 1,1

x= 2000 руб.– сумма, которая снимается со вклада

Для запланированной суммы

Год	Вклад	Вклад с процентами
1	S	Sb
2	Sb	Sb²
3	Sb²	Sb³

 

 

 

Для фактической суммы

Год	Вклад	Вклад с процентами	Остаток
1	S	Sb	Sb - x
2	Sb - x	Sb² - bx	Sb² - bx +x
3	Sb² - bx +x	Sb³ - b²x +bx

 

Разница между запланированной и фактической суммой равна

Sb³ - (Sb³ - b²x +bx) = b²x  - bx = 1,1²×2000 – 1,1×2000= 220 руб.

То есть, вкладчик получит на 220 руб. меньше запланированной суммы
Ответ: 220 руб.

Решение.

Пусть S = 400000 руб. – изначальная сумма вклада

r  = 12,5% - ежегодная процентная ставка

b = 1 +  – коэффициент, на который умножается основная сумма вклада

b = 1,125

m – сумма, на которую пополняется вклад

Год	Основная сумма вклада	Платеж	Сумма вклада с процентами
1	S	-	Sb
2	Sb	-	Sb²
3	Sb²	m	Sb³+mb
4	Sb³+mb	m	Sb⁴+mb²+mb

 

Так как сумма на вкладе к четвертому году должна быть не меньше должна быть не меньше 7000000 руб.,

Sb⁴+mb²+mb >700000

m(b²+b)>700000 - Sb⁴

m >

m > 24795,751633…руб.

Так как m – целое число, m минимальное равно 25 тысяч рублей
Ответ: 25 тысяч руб.

Задания для самостоятельного решения

1.     Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?

2.     Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей?

3.     Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?

 

 

 

 

 

 

Ответы.

§ 1.

1. на 9 месяцев.

2. 2 296 350 руб.

3. 806400 руб.

§ 2.

1. 120 %.

2. 3%.

3.20%.

§ 3.

1. Маша, на 1100 рублей.

2. у Саши, на 1155 рублей.

3. 240 тыс. рублей.

 

 

 

 

 

 

 

 

 

 

 

 

Литература

1.     Математика. Подготовка к ЕГЭ 2020. Профильный уровень. 40 тренировочных вариантов по демоверсии 2020 года : учебно-методическое пособие / под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион, 2019. – 416с. – (ЕГЭ)

2.     Алгебра : 9 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М. : Вентана-Граф, 2018. – 304 с. : ил.

3.     ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под редакцией И.В. Ященко. – М. :  Издательство «Национальное образование», 2019. – 256с. – (ЕГЭ. ФКР – школе)

4.     Решу ЕГЭ Дмитрий Гущин.

 https://math-ege.sdamgia.ru/test?theme=221

5.     ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под редакцией И.В. Ященко. – М. :  Издательство «Национальное образование», 2020. – 256с. – (ЕГЭ. ФКР – школе)

 

Скачано с www.znanio.ru