Задача скачана с сайта www.MatBuro.ru

Решебник Чудесенко по теории вероятностей и математической статистике ©МатБюро - Решение задач по математике, экономике, статистике

Тема: Геометрическая вероятность (Чудесенко, задача 6, вариант 6)

ЗАДАНИЕ. Моменты начала двух событий наудачу распределены в промежутке времени от ^T₁ до ^T₂ . Одно из событий длится 10 мин., другое – t мин. Определить вероятность того, что: а) события «перекрываются» по времени; б) «не перекрываются». T₁=1100; ^T₂ =1300; t=15

РЕШЕНИЕ.

Используем для решения задачи геометрическое определение вероятности.

Обозначим моменты начала первого и второго события за x и y . Так как события поступают в промежуток  T₁ до T₂ , то справедливы следующие условия: T x y T₁ ≤ , ≤ ₂ .

Рассмотрим прямоугольную систему координат xOy . В этой системе координат всем возможным значениям времени начала событий соответствуют точки квадрата со стороной T T₂ − ₁ =1300−1100 = 200 (см. рисунок). 

Закрашенная область S соответствует тем моментам начала событий, при которых они «перекрываются», так как между началами событий проходит не больше времени, чем длится событие (самое первое). 

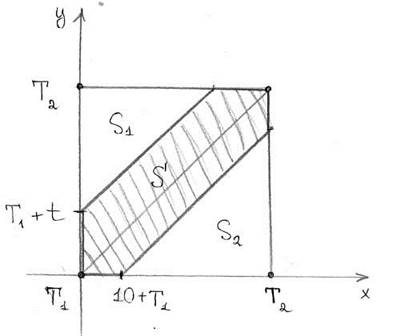
Тогда по геометрическому определению вероятности вероятность события A =(События «перекрываются» во времени) равна отношению площади заштрихованной фигуры к площади всего квадрата. Площадь фигуры вычислим как площадь квадрата минус площади двух равнобедренных прямоугольных треугольника:

Задача скачана с сайта www.MatBuro.ru

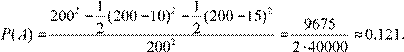
Решебник Чудесенко по теории вероятностей и математической статистике ©МатБюро - Решение задач по математике, экономике, статистике

Вероятность противоположного события A =(События не «перекрываются» во времени)

равна P A( ) = −1 P A( ) = −1 0,121= 0,879 .

ОТВЕТ: 0,121; 0,879.