Доклад на тему: «Роль игровых технологий на уроках математики»

 

 

 

МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ 

« СРЕДНЯЯ БЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №19 им. Л.А. ПОПУГАЕВОЙ»

             Г. УДАЧНЫЙ   МИРНИНСКОГО МУНИЦИПАЛЬНОГО  РАЙОНА

 

 

 

 

 

 

 

 

Доклад

 

«Роль игровых технологий на уроках математики»

 

 

Выполнил

Учитель математики МАОУ                         «СОШ №19 им. Л.А. Попугаевой»

Деева Наталья Александровна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2023 год

 

 

 

«Игра – это огромное светлое окно,

 через которое в духовный мир ребёнка

 вливается живительный поток

 представлений, понятий об окружающем мире

Игра – это искра, зажигающая огонёк пытливости и любознательности.»

(В.А.Сухомлинский.)

 

        В связи с увеличением умственной нагрузки на уроках математики необходимо задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. Как можно заставить учащихся поверить в свои силы?

 

В связи с этим, основная задача, которую я ставлю перед собой, заключается в том, чтобы отыскать новые эффективные методы обучения и такие методические приемы, которые активизировали бы мысль школьников, стимулировали бы их к самостоятельному приобретению знаний. И таким методом, безусловно, является применение игровых технологий на уроках математики.

 

        Данная проблема широко рассмотрена в работе В. А. Сухомлинского “О воспитании”. В этой книге он знакомит нас со своими мыслями о воспитании детей в семье и в школе, в том числе автор пишет об использовании игры: “…Игра – это огромное светлое окно, через которое в духовный мир ребёнка вливается живительный поток представлений, понятий об окружающем мире. Игра – это искра, зажигающая огонёк пытливости и любознательности”. Продолжая работу Сухомлинского, в своей работе “Психология игры” Д. Б. Эльконин пишет, что игра влияет на развитие психических процессов: “Значение игры не ограничивается тем, что у ребёнка возникают новые по своему содержанию мотивы деятельности и связанные с ними задачи. В игре возникает новая психологическая форма мотивов

         Возникновение интереса к математике у значительного числа учащихся зависит в большей степени от методики преподавания, от того, насколько умело будет построена учебная работа. Необходимо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности, творческого интереса и глубокого познавательного интереса. 5Познавательный интерес –это соединение психических процессов: ; интеллектуальная деятельность; эмоциональные проявления; волевые проявления.

Это особенно важно в подростковом возрасте, когда еще формируются, а иногда и только определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрывать притягательные стороны математики.

 

        Игры на уроках математики, считаю современным методом обучения и воспитания, обладающим образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. В играх различные знания и новые сведения ученик получает свободно. Поэтому часто то, что на уроке казалось трудным, даже недостижимым, во время игры легко усваивается. Здесь интерес и удовольствие – важные психологические показатели игры.

 

       Основная цель моей работы – активизация познавательной деятельности учащихся на уроках математики, развитие любознательности и глубокого познавательного интереса к предмету через игровую деятельность. Ведь игра – это вид деятельности в условиях ситуаций, направленных на воссоздание и усвоение общественного опыта, в котором складывается и совершенствуется самоуправление поведением. Мотивация игровой

 

деятельности обеспечивается её добровольностью, возможностями выбора и элементами соревнования, удовлетворения потребности в самоутверждении, самореализации.

 

Считаю, что математическая игра помогает закреплять и расширять предусмотренные школьной программой знания, умения и навыки.

Математическая игра, включенная в занятие, и просто игровая деятельность в процессе обучения оказывают заметное влияние на деятельность учащихся. Игровой мотив является действительным подкреплением познавательному мотиву, способствует созданию дополнительных условий для активной мыслительной деятельности учащихся, повышает концентрированность внимания, настойчивость, работоспособность, создает дополнительные условия для появления радости успеха, удовлетворенности, чувства коллективизма.

Актуальность применения игровых технологий на уроках математики :

-игровые формы обучения на уроках создают возможности

эффективной организации взаимодействия педагога и учащихся, продуктивной формы их общения с присущими их элементами соревнования;

-в игре заложены огромные воспитательные и образовательные возможности

-игры очень хорошо уживаются с «серьёзным» учением;

-включение в урок игр делает процесс обучения интересным и занимательным, облегчает преодоление трудностей в усвоении учебного материала

-разнообразные игровые действия ,при помощи которых решается та или иная умственная задача , поддерживают и усиливают интерес к учебному предмету.

Математическая игра: цели, задачи, функции и требования.

Цели применения математических игр:

• развитие мышления;
• углубление теоретических знаний;
• самоопределение в мире увлечений и профессий;
• организация свободного времени;
• общение со сверстниками;
• воспитание сотрудничества и коллективизма;
• приобретение новых знаний, умений и навыков;
• формирование адекватной самооценки;
• развитие волевых качеств;
• контроль знаний;
• мотивация учебной деятельности

 

Задачи математических игр:

1. образовательные:

• способствовать прочному усвоению учащимися учебного материала;
• способствовать расширению кругозора учащихся и др.
• 2. развивающие:

• развивать у учащихся творческое мышление;
• способствовать практическому применению умений и навыков, полученных на уроках и внеклассных занятиях;
• способствовать развитию воображения, фантазии, творческих способностей и др.

3.воспитательные:

• способствовать воспитанию развивающейся и реализующейся личности;
• воспитать нравственные взгляды и убеждения;
• способствовать воспитанию самостоятельности и воли в работе.

 

 

 

Функции математических игр:

1.Во время математической игры происходит одновременно игровая, учебная и трудовая деятельность. Действительно, игра сближает то, что в жизни не сопоставимо и разводит то, что считается едино.

2.Математическая игра требует от школьника, то чтобы он знал предмет. Ведь не умея решать задачи, разгадывать, расшифровывать и распутывать ученик не сможет участвовать в игре.

3.В играх ученики учатся планировать свою работу, оценивать результаты не только чужой, но и своей деятельности, проявлять смекалку при решении задач, творчески подходить к любому заданию, использовать и подбирать нужный материал.

4.Результаты игр показывают школьникам их уровень подготовленности. Математические игры помогают в самосовершенствовании учащихся и, тем самым побуждают их познавательную активность, повышается интерес к предмету.

5.Во время участия в математических играх учащиеся не только получают новую информацию, но и приобретают опыт сбора нужной информации и правильного ее применения.

Требования к игровым урокам

 

      К участникам математической игры должны предъявляться определенные требования в отношении знаний. В частности, чтобы играть – надо знать. Это требование придает игре познавательный характер.

 Правила игры должны быть такими, чтобы учащиеся проявили желание поучаствовать в ней. Поэтому игры должны разрабатываться с учетом возрастных особенностей детей, проявляемых ими интересов в том или ином возрасте, их развития и имеющихся знаний.

 Математические игры должны разрабатываться с учетом индивидуальных особенностей учащихся, с учетом различных групп учащихся: слабые, сильные; активные, пассивные и др. Они должны быть такими, чтобы каждый тип учащихся смог проявить себя в игре, показать свои способности, возможности, свою самостоятельность, настойчивость, смекалку, испытать чувство удовлетворенности, успеха.

 При разработке игры нужно предусмотреть более легкие варианты игры, задания для слабых учащихся и, наоборот, более сложный вариант для сильных учеников. Для совсем слабых учащихся разрабатываются игры, где не нужно думать, а нужна, лишь смекалка. .

          Математические игры должны разрабатываться с учетом предмета и его материала. Они должны быть разнообразны. Многообразие видов математических игр поможет повысить эффективность урока математики, послужит дополнительным источником систематических и прочных знаний.

 Таким образом не только сильные учащиеся е проявляют заинтересованность к предмету, но и слабые учащиеся начинают проявлять свою активность в учении.

Виды математических игр:

• игры-упражнения;
• игры-путешествия;
• сюжетная ролевая игра:
• игра-соревнование.

Игры-упражнения занимают обычно 10-15 минут и направлены на совершенствование познавательных способностей учащихся, осмысления и закрепления учебного материала,Это разнообразные викторины ,кроссворды, ребусы,шарады, головоломки ,загадки.

Игры-путешествия служат, в основном ,целям углубления , осмысления и закрепления учебного материала.

 

 

 

Сюжетная игра отличается тем ,что инсценируются условия воображаемой ситуации., а учащиеся играют определённые роли.

Игра-соревнование ,Существенной особенностью игры-соревнования является наличие в ней соревновательной борьбы и сотрудничества.Элементы соревнования занимают ведущее место в основных игровых действиях,а сотрудничество,как правило,определяется конкретными обстоятельствами и задачами.

Игра-соревнование позволяет учителю в зависимости от содержания материала вводить в игру не просто занимательный материал ,но весьма сложные вопросы учебной программы.

 Классификация математических игр по назначению.

 По назначению различают: обучающие, контролирующие и воспитывающие игры. Также можно выделить развивающие и занимательные.

 Участвуя в обучающей игре, школьники приобретают новые знания, навыки. Так же такая игра может служить стимулом для получения новых знаний: ученики вынуждены приобрести новые знания перед игрой; очень заинтересовавшись каким-либо материалом, полученным на игре, ученик может изучить его подробнее уже самостоятельно.

         Воспитывающая игра имеет целью воспитать у учащихся отдельные качества личности, такие как: внимание, наблюдательность, смекалка, самостоятельность и др.

 Для участия в контролирующей игре учащимся достаточно имеющихся у них знаний. Цель такой игры и состоит в том, чтобы школьники закрепили свои полученные знания, проконтролировать их.

         Занимательные игры отличаются от других видов тем, что для участия в ней никаких конкретных знаний не надо, нужна только смекалка. Основная цель такой игры - это привлечь к математике слабых учеников, не проявляющих интереса к предмету.

 И последний вид в этой классификации, это развивающие игры. Они в основном предназначены для сильных учеников, увлекающихся математикой. Они развивают нестандартность мышления при решении соответствующих заданий.

 Все эти виды переплетаются между собой, и одна игра может быть одновременно и контролирующей, и обучающей, лишь в соотношении между целями можно говорить о принадлежности математической игры к тому или иному виду.

По массовости различают коллективные и индивидуальные игры.

 Игры чаще всего принимают коллективный характер. Они привлекают не только сильных учеников, но и слабых, желающих поучаствовать в игре вместе со своими друзьями. Такие ученики, не проявляющие интереса к математике, в коллективной игре могут добиться успеха, у них появляется чувство удовлетворенности, интерес.

 С другой же стороны, сильные ученики предпочитают индивидуальные игры, так как они более самостоятельны. Они стремятся к самоанализу, самооценке, и поэтому у них возникает потребность проявить свои индивидуальные возможности, качества.

 

 По реакции выделяют подвижные и тихие игры.

 Основной деятельностью учащихся является учеба. Они проводят в школе 5 - 6 часов в день в школе, и дома 2-3 часа уходит на выполнение домашнего задания. Естественно, что их растущий организм требует движения, поэтому на занятиях нужно вводить элементы подвижности.

 Математическая игра позволяет включить в себя подвижную деятельность и не мешает умственной работе.       Встречаются дети, которые предпочитают тихие игры, требующие пытливости ума, настойчивости. Для таких детей подойдут тихие игры, такие как различные головоломки, кроссворды, игры на складывание и разрезание фигур, и многие другие.

 

 

 

По темпу выделяют скоростные и качественные игры.

 Некоторые математические игры должны принимать форму состязаний, соревнований между командами или на личное первенство, это обусловлено характерной чертой подростков, стремления к различным видам состязаний.

 Следует различать два вида состязаний. Во-первых, это игры, в которых победа достигается за счет скорости действий, но это без ущерба качеству решения задач. Например, задания на скорость выполнения вычислений, преобразований, доказательств теорем и т. д. Такие игры называются скоростными. Во-вторых, так же можно выделить игры, победа в которых достигается не за счет скорости выполнения заданий, а за счет качества его выполнения, правильности решения, безошибочности. Такие игры условно называют качественными.

 Первый вид игр (скоростные) необходим, когда нужен автоматизм действий, формируется навык быстрого вычисления, выполнения действий, не требующих большого умственного труда. Также элементы скоростных игр могут быть включены в другие математические игры. Использование таких игр сопровождается эмоциональным подъемом, желанием выиграть, стремлением быть не только лучшими, но и самым быстрым, вызывает интерес учащихся.

 Качественные же игры направлены на серьезные вычисления, требует вдумчивой работы над трудными задачами, теоремами. Такие игры способствуют пробуждению мыслительной деятельности учащихся, заставляют их активно думать над задачей, развивают настойчивость, упорство, что необходимо в учебе. Неразрешимые, казалось бы, сложные задачи способствуют повышению умственного труда, упорства, и, как следствие, желанию узнать больше, появлению интереса к предмету.

 

        Выводы

 

Задача учителя организовать процесс обучения таким образом, чтобы каждое усилие по овладению знаниями протекало в условиях развития познавательных способностей учащихся, формирование у них таких основных приёмов умственной деятельности, как: анализ, синтез, абстрагирование, обобщение, сравнение. Считаю, что учитель должен восхищаться красотой и мощью математических методов и заражать этим своих учеников. Помнить, что встречаясь даже с одарёнными учениками, он готовит из него не математика, а прежде всего, всесторонне развитую личность, ведь в процессе обучения в школе формируется человеческое сознание, взгляд, мировозрение , убеждения, творческие способности.

 Игровые технологии используются на уроках в следующих случаях: в качестве самостоятельной технологии для освоения понятия, темы или даже раздела учебного предмета; как элемент более обширной технологии; в качестве урока или его части; как технология внеклассной работы. Уроки, проводимые мною с применением игровой технологии, приведены ниже.

 И закончить хочется словами великого русского писателя Л. Н. Толстого: «Если ученик в школе не научился сам ничего творить, то в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы научившись копировать, умели сделать самостоятельное приложение этих сведений».

 

 Игровые ситуации на уроках математики

 

Привожу некоторые примеры использования дидактических игр на уроках математики в 5-6 классах. Работаю по учебнику Н.Я. Виленкин и др.

Пример 1.

 

 

 Тема «Прямоугольная система координат на плоскости» (6 класс)

Игра «Соревнование художников»

 На доске записаны координаты точек: (0;0),(-1;1),(-3;1),(-2;3),(-3;3),(-4;6),(0;8),(2;5),(2;11),(6;10),(3;9),(4;5),(3;0),(2;0),(1;-7),(3;-8),(0;-8),(0;0).

 Отметить на координатной плоскости каждую точку и соединить с предыдущей отрезком. Результат – определенный рисунок.

 Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.

 Эта игра очень нравится учащимся.

Игра «Морской бой» тоже нравиться учащимся.

 Эти игры развивают внимание, наблюдательность, сообразительность, ученики быстрее усваивают и убеждаются, что положение точки на плоскости определяется с помощью двух её координат.

Пример 2.

 Тема «Действия с целыми числами» (6 класс)

Игра «Математическое лото»

 Каждому ученику выдается конверт, в котором 1 большая карта с заданиями и маленькие, их больше, чем заданий. На маленьких – результаты вычислений. Ученик должен выполнить задание на большой карте и накрыть его ответом (результатом его вычислений). После выполнения всех заданий ученик переворачивает маленькие карточки и получает задание (если верно выполнены все вычисления). Например: определение целых чисел, правило сравнения, правило сложения, вычисление, деление, умножения целых чисел и др. Затем ученики выполняют полученные задания.

 

Игра «Магические квадраты»

 А) В клетки квадрата записать такие числа, чтобы сумма чисел по любой вертикали, горизонтали была равна 0.

 

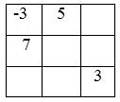
Б) Записать в клетки квадрата числа -1; 2; -3; -4; 5; -6; -7; 8; -9 так, чтобы произведение по любой диагонали, вертикали, горизонтали было равно положительному числу.

 

Игра «Забег по кругу»

 

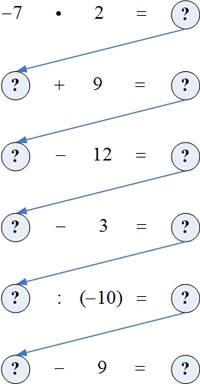
На доске записана цепочка примеров, которые нужно выполнить строго по указанию стрелки. При правильном выполнении заданий получают первое число цепочки.

 Эти игры помогают усвоить все действия с целыми числами, вычислительные навыки, сообразительность, внимательность.

Пример 3.

 Тема «Десятичные дроби»

Игра «Цветочек»

 В листе цветка помещается дробь, которую нужно сложить, умножить, разделить, вычесть. Дроби, с которыми нужно произвести эти действия, записаны на лепестках цветка.

 

 

 

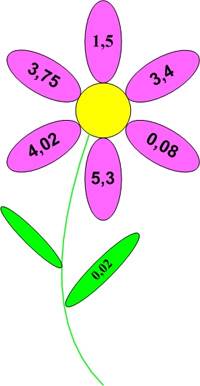
1) 1,5 ∙ 0,2

 2) 3,75 ∙ 0,2

 3) 3,4 : 0,2

 4) 0,08 + 0,2

 5) 4,02 + 0,2

 6) 5,3 – 0,2

 После того, когда ученики выполнят указанные действия, рисует на доске такой же цветок тот, кто первым выполняет все вычисления, только в лепестках пишет результаты вычислений.

Пример 4.

 Тема «Признаки делимости чисел»

Игра «Лучший счетчик»

 Класс делится на три команды. Каждая выбирает «счетчика», который будет защищать свою команду. Примеры «счетчику» задают члены других команд до тех пор, пока он не собьется. Затем его сменяет «счетчик» другой команды. За каждый правильный ответ 1 очко. Побеждает команда, которая набрала больше очков. Условие игры – отвечать на вопросы быстро.

 В ходе игры вырабатывается быстрота вычислений, внимательность, сообразительность.

 Основным в дидактической игре на уроках математики является обучение математике. Игровые ситуации лишь активизируют деятельность учащихся, делают восприятие более активным, эмоциональным, творческим. Создание игровых ситуаций на уроках повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебной работе, снижает утомление, развивает внимание, взаимопомощь.

 Дидактические игры влияют на повышение качества знаний, умений и навыков

учащихся, развитие умственной деятельности.