Муниципальное казенное общеобразовательное учреждение

«Туршунайская общеобразовательная школа»

 

 

 

 

 

ДОКЛАД

на тему

«Развитие познавательного

интереса учащихся 5-9 классов на уроках математики  и

во внеурочное время»

Доклад на семинаре учителей математики

 

Подготовила: Джанакавова Б.М.,

учитель математики

 МКОУ «Туршунайская СОШ»

 

 

 

2019 год

 

Величие человека - в его способности мыслить.

(Б. Паскаль)

Введение

 

Проблема интереса в обучении не нова. Значение его утверждали многие дидакты прошлого. В самых разнообразных трактовках проблемы в классической педагогике главную функцию его все видели в том, чтобы приблизить ученика к учению, приохотить, «зацепить» так, чтобы учение для ученика стало желанным, потребностью, без удовлетворения которой немыслимо его благополучное формирование.

Ян Амос Коменский, совершивший революцию в дидактике, рассматривая новую школу как источник радости, света и знания, считал интерес одним из главных путей создания этой светлой и радостной обстановки обучения.                  Ж.-Ж. Руссо, опираясь на непосредственный интерес воспитанника к окружающим его предметам и явлениям, пытался строить доступное и приятное ребенку обучение. К. Д. Ушинский в интересе видел основной внутренний механизм успешного учения. Он показал, что внешний механизм приневоливания не достигает нужного результата. Даже И. Ф. Гербарт, признавая интерес имманентным, свойством, призывал учителя не быть скучным, а основывать обучение на интересах, присущих ребенку.

Весь многовековой опыт прошлого дает основание утверждать, что интерес в обучении представляет собой важный и благоприятный фактор его построения.

Современная дидактика, опираясь на новейшие достижения педагогики и психологии, видит в интересе еще большие возможности и для обучения, и для развития, и для формирования личности ученика в целом.

Я работаю в сельской школе в классах с малой накопляемостью,  учащимися разных способностей и возможностей. Из своего опыта работы я знаю, что среди  всех мотивов учебной деятельности самым действенным является познавательный интерес. Первичной формой познавательного интереса является любопытство, затем появляются любознательность и увлеченность предметом. Познавательный интерес, возникающий в процессе обучения, активизирует умственную деятельность не только в данный момент, но и  направляет её к последующему решению различных  интеллектуальных задач. Формируется устойчивый познавательный  интерес не сразу и разными средствами. Одним из них является занимательность. Прежде всего элементы занимательности вызывают богатое своими последствиями чувство удивления: это  могут быть новизна, необычность, странность, противоречивость прежним  представлениям, неожиданность  и т.д. А роль эмоций в процессе познания  очевидна.

Познавательный  интерес побуждает подростка не только к восприятию определенного учебного материала, но, что  особенно важно для обучения, располагает его к самостоятельной учебной деятельности, которая, в свою очередь, в состоянии удовлетворять и поддерживать его познавательный интерес;  обусловливает создание таких условий,  благодаря которым процесс деятельности становится более активным, творческим; сам характер деятельности ученика может стать стимулом для укрепления появившегося интереса.

Ученик может получать постоянно хорошие оценки по математике, но это еще не свидетельствует об интересе его к предмету. Другой школьник может получать удовлетворительные оценки, однако это не говорит об отсутствии у него интереса к предмету. Первому ученику легко дается учение, но, возможно, он не проявляет интереса к математике. Второму ученику учение дается не очень легко, но, возможно, ему интересно учиться. Оценка чаще всего показывает успехи и старания в изучении данного предмета. Одна только оценка не может являться признаком наличия интереса к этому предмету.

Из опыта работы я сделала вывод,  что интерес к математике  может возникать у учащегося, слабо успевающего по предмету. Я  вижу его  затруднения, связанные с плохим знанием теоретического материала за прошлые годы или с неумением быстро и умело проводит вычисления, преобразования и рассуждения, помогаю ему  и поддерживаю появившийся у него  интерес к математике.

Некоторые ученики, не проявлявшие ранее особых успехов в математике, показывали мне свои решения задач, которые задавались более способным ученикам. Я стала предлагать им нестандартные задачи, которые решали и отличники. Очень часто эти ученики справлялись с заданием одновременно с отличниками, а иногда и раньше их, нередко представляли оригинальные решения.

Поддержка учащихся, ранее не отличавшихся знаниями, но неожиданно проявившиеся себя в нескольких случаях как умеющих мыслить не стандартно, поднимал их авторитет перед учениками класса и вдохновлял на дальнейшее более серьезное изучение предмета. Здесь, по моему мнению, имеет место не гласное соревнование.

Учащиеся часто задают мне вопросы, которые могут возникнуть в результате личных наблюдений и размышлений или в результате чтения дополнительной литературы. Ни один вопрос не остаётся без ответа, в тоже время каждый учащийся заслуживает похвалу за хорошую постановку вопроса. Иногда я рекомендую  математическую литературу, в которой можно получить исчерпывающий ответ на интересующий ученика вопрос, так как это лучший способ  поддержания интереса к предмету, формирования самостоятельности поиска.

Я считаю, что интерес играет главную роль в учебной деятельности. Осознанное, планируемое создание условий для развития познавательного интереса – это одно из сильных средств повышения эффективности обучения на уроке математике.

 

 

Основные формы и методы формирования познавательного интереса учащихся на уроках математики

 

Уровни развития познавательного интереса

 

У школьников одного и того же класса познавательный интерес может иметь разный уровень своего развития и различный характер проявлений, обусловленных различным опытом, особыми путями индивидуального развития. Элементарным уровнем познавательного интереса можно считать открытый, непосредственный интерес к новым фактам, к занимательным явлениям, которые фигурируют в информации, получаемой учениками на уроке.

Более высоким уровнем его является интерес к познанию существенных свойств предметов или явлений, составляющих более глубокую и часто невидимую их внутреннюю суть. Этот уровень требует поиска, догадки, активного оперирования имеющимися знаниями, приобретенными способами.

На этом уровне познавательный интерес часто связан с решением задач прикладного характера, в которых школьника интересует не столько принцип действия, сколько механизм, при помощи которого оно происходит. На этом уровне интерес уже не находится на поверхности отдельных фактов, но еще не проникает настолько в познание, чтобы обнаружить закономерности. Этот уровень, пожалуй, можно назвать стадией описательства, в которой фиксация внешних признаков и существенных свойств изучаемого находится на равных началах. Эта стадия характерна для младших подростков, которые еще не имеют достаточного теоретического багажа, чтобы проникнуть в суть и глубь вещей, но уже оторвались от элементарных конкретных действий и становятся способными к самостоятельному дедуктивному подходу в изучении.

Еще более высокий уровень познавательного интереса составляет интерес школьника к причинно-следственным связям, к выявлению закономерностей, к установлению общих принципов явлений, действующих в различных условиях. Этот уровень бывает сопряжен с элементами исследовательской творческой деятельности, с приобретением новых и совершенствованием прежних способов учения. На этом уровне в учебном процессе особенно ощутимо движение ученика, который обнаруживает не только схватывание общего смысла, но и глубокое опосредованное осознание самых важных, существенных сторон изучаемого, который способен видеть диалектику явлений, обнаруживать глубокий интерес  к познанию закономерностей. Указанные уровни познавательного интереса довольно обобщенно рисуют нам тенденции его развития.

 

 

 

Содержание  учебного материала как источник стимуляции

познавательного интереса

 

Стимуляция познавательных интересов школьников поступает из различных источников. Она поступает из содержания учебного материала, которое несет учащимся  новую, неизвестную еще ранее информацию, вызывающую чувство удивления перед тем, как богат мир и как мало он еще открыт ему, ученику, и как заманчиво и увлекательно познавать это новое на каждом уроке.

Содержание знаний заключает в себе и возможности по-новому проникнуть в уже известное, открывать в имеющихся знаниях новые грани, рассматривать их под новым углом зрения и испытывать при этом глубочайшее чувство удовлетворения от того, что теперь ты знаешь предмет лучше, глубже и основательней.

Содержание знаний позволяет проникать в тайники науки от момента ее зарождения до современных научных достижений, открытий, переворачивающих весь арсенал научных знаний, добытый ранее. Содержание знаний несет в себе и такой важный стимул познавательного интереса, как осознание и понимание практической роли познания.

 

 

Постановка текстовых задач как один из способов повышения интереса учащихся к математике

Задачи прикладного содержания

Одним из способов повышения интереса к математике у учащихся является усиление практической направленности преподавания.

В.Г. Болтянский писал, что «задачи прикладного характера имеют в общеобразовательной школе важное  значение для воспитания интереса к математике. На примере хорошо составленных задач прикладного содержания  учащиеся убеждаются в значении  математики для различных сфер человеческой деятельности, в ее пользе и необходимости для практической работы, увидят широту возможных  приложений математики, поймут ее роль в современной культуре.

Приведу пример задачи.

В распоряжении бригадира имеются два тракториста. Производительность труда первого тракториста равна 15 га/ч, второго – 20га/ч. Площадь поля равна 240 га. Через сколько часов после начала работы первого тракториста к нему должен присоединиться второй, чтобы поле было обработано за 8 часов.

Творческие задания

Работая в сельской школе, нельзя строить урок на одних только сложных заданиях, которые оказываются обычно непосильными для большей половины класса. Обучение, вовлекающее в творческую работу весь класс, должно проходить на легком материале. Но этот материал должен быть подан разнообразно не столько в математическом, сколько в методическом плане. Под методическим разнообразием имеется в виду следующее: формулировка задачи должна содержать конфликт, который виден учащемуся сразу, без обращения к математической стороне вопроса. К задачам такого рода часто относят следующие:

• задачи, где предлагаются ошибочные рассуждения или нереальные конфигурации и требуется найти ошибку и исправить ее;

• задачи, в которых по предлагаемым данным нужно отыскать все, что возможно (т.е. учащиеся вынуждены сами формулировать цели своей работы);

Приведу пример  задач указанных видов при повторении темы «Четырехугольники» и «Теорема Пифагора».

Задача 1.Найдите ошибки на рис.1, а-г.

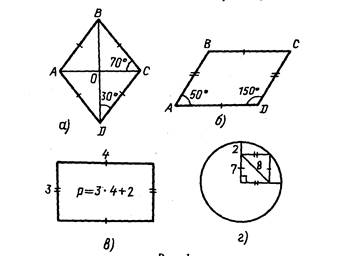
                                  Рис.1.

Рассмотрев рис. 1, учащиеся установят, что треугольники ВОС и DОС равны и, значит, угол DСО составляет 70°, а тогда угол СОD равен 80°, что противоречит перпендикулярности диагоналей ромба.

На рис. 1, г ошибочно показаны неравными смежные стороны квадрата и неправильно указана его диагональ. Это один из самых трудных случаев, поскольку здесь скрыты сразу две трудности, и одна из них графического плана. В предыдущих заданиях ребята встречались с ошибками лишь метрического характера: или с неправильно измеренными углами параллелограмма (рис. 1, б), или с ошибочно подсчитанным периметром (рис. 1, в).

Задача 2. Определите вид треугольников на рис. 2, а, б. Узнайте о них  все, что возможно.

Прежде всего учащиеся должны понять, что на рис. 2, а дан равносторонний треугольник, имеющий три угла по 60°. Отсюда остается сделать простейшие логические шаги до нахождения длины отрезка АС, а затем периметра треугольника АВС. По рис. 2, б ребята вычислят второй острый угол, гипотенузу, второй катет, а затем смогут найти периметр и площадь данного треугольника.

 

 

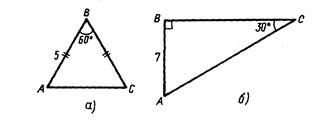
                     Рис.2.

 

Как видно, задания нетрудные. Но все дело в том, что этих заданий учащимся никто непосредственно не предлагает. Они сами ставят перед собою маленькие цели, продвигаясь в том порядке, какой им кажется наиболее разумным. Вот так и оттачивается то, что в дальнейшем сложится в умение находить верный путь решения.

 

Поисковые задания

 

Поисковые задания должны быть ориентированы на всех учащихся. Они должны быть доступны для каждого ученика и в то же время способны быть эффективным средством для развития творческих способностей. Поисковые задания, применяемые мною, тесно связаны с основным учебным материалом.

 Приведу пример задач к теме «Смежные углы» по геометрии 7-го класса.

1.По рис. 1 составьте задачу, в которой бы требовалось найти величины смежных углов. Решите ее.

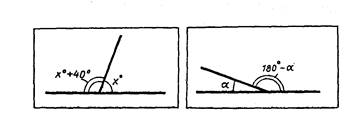
                Рис.1.                         Рис.2.

 

 

2. Составьте задачу на нахождение величин смежных углов, которая бы сводилась к решению уравнения х+ (х-20) = 180. Решите ее.

3. Составьте задачу на нахождение величин смежных углов, которая бы сводилась к решению уравнения х+5х=180. Решите ее.

4.Смежные углы равны α и 180° — α (рис. 2). Над этими величинами выполним следующие действия:

1) α⁄2; 180°-α/2

2) α⁄2+ 180°- α⁄2 =90°.

Получили угол, равный 90°. Что это за угол? Изобразите его на рис. 2. Какую геометрическую закономерность вы заметили? Сформулируйте ее.

Из опыта своей работы я могу сказать что, применение поисковых заданий снижает подражание,  действовать по образцу, развивает способность к преобразованию математических объектов, критическому осмыслению способов решения задач.

 

Задачи, реализующие межпредметную связь

 

При решении в 5-6  классах математических задач, имеющих неинтересные и не несущие какой-либо информации тексты, часто наблюдается у учащихся быстрое утомление, а вследствие этого — потеря интереса к решению задач. Это, естественно, снижает эффективность работы учащихся.

С этой целью я применяю задачи, содержание которых связано с материалом, изучаемым по другим дисциплинам. Приведу пример задачи такого типа.

Историко - математическая задача.

Чтобы спуститься с Везувия, спартаковцы сплели лестницу, 875 м которой были сделаны из пеньковых веревок. Часть лестницы, выполненной из ивовых прутьев, составляла 20 % от длины веревочной части, а остальные 321 м были сделаны из виноградных лоз. Какова высота Везувия? О т в е т: 1371 м.

Дифференцированное обучение

 

Дифференцированный подход в обучении  играет важную роль в развитии познавательного интереса у учащихся. Для учащихся разных способностей ставлю различные цели: одни ученики должны достичь определенного уровня математической подготовки, называемого базовым, а другие, проявляющие интерес к математике и обладающие хорошими математическими способностями должны добиться более высоких результатов.  

В соответствии с этим в классе выделяю две группы учащихся: группа базового уровня и группа повышенного уровня.

Дифференцированный подход я   осуществляю на определенных этапах урока. На этапе введения нового понятия, свойства, алгоритма я работаю со всем классом, без деления его на группы. Но после того, как несколько упражнений выполнено на доске,  учащиеся могут приступить к дифференцированной самостоятельной работе.  Её особенность состоит в том, что группа базового уровня и группа повышенного уровня получают задания, различающиеся не только содержанием, но и формой их подачи.

Приведу пример разноуровневых заданий.

I вариант.

Коля сделал 27 деталей за 3ч, а Петя 20 деталей за 2,5ч. У кого из них производительность выше ?

II вариант.

Коля может выполнить всю работу за 3ч, Петя – за 4ч, Вася – за 5ч, Дима – за 6ч. Кто быстрее выполнит работу: Коля вместе с Димой, или Петя вместе с Васей ?

Таким образом, разноуровневые задания, составленные с учетом возможностей учащихся, создают в классе благоприятный  психологический климат. У ребят возникает чувство удовлетворения после каждого  верно решенного задания. Успех, испытанный в результате преодоления трудностей, дает мощный импульс к повышению познавательной активности. У учащихся, в том числе и у слабых,  появляется уверенность в своих силах, они уже не чувствуют страха перед новыми задачами, пробуют свои силы в незнакомой ситуации.

 

Нетрадиционные формы повторения

 

Работая  в сельской школе, я убедилась, что без повторения нет учения, однако осуществлять повторение нужно не только на зачетах в конце темы, но и ежеурочно. Именно ежедневные повторения закрепляют знания учащихся, и организовывать их нужно разными методами, не жалея на это ни сил, ни времени, ни творческой энергии. Например: математическая гармошка.

«Гармошкой» я называю обычную тетрадку-раскладушку, которые дети мастерят сами по моей просьбе. Такая гармошка должна быть у каждого ученика. В ней каждая полоса посвящена какой-либо одной теме. Например, на одной полосе записываются единицы измерения, на другой — формулы приведения, на третьей — формулы для вычисления периметра и площади прямоугольника и т.д. Приведу пример такой гармошки.

Ребята любят свои гармошки, с удовольствием их мастерят, делают в них аккуратные записи, и такие гармошки действительно помогают им и задачи решить, и весь курс усвоить.

В середине урока, когда ребята уже немного устали, я часто им говорю: «Поиграем на гармошке», быстро задаю вопросы по изученному материалу:

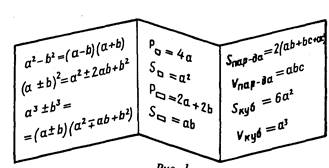
«Как найти объем куба? Чему равна разность квадратов двух чисел? Вопросы идут в разбивку, не всякий быстро сориентируется даже с помощью гармошки, а я доказываю ребятам, что быстрее отвечает тот, кто хорошо помнит, что у него в гармошке записано, т.е. кто материал лучше знает, тот и на гармошке веселей играет.

Игровые формы урока

 

Для успешного усвоения знаний, их отработки, я применяю игровые формы уроков.  Игра  приносит удовольствие, наслаждение, радость от получения новых знаний, наслаждение от осознания ребенком того, что он стал умнее, радость от победы в интеллектуальной игре.

Я приведу примеры  игровых форм проведения урока при закреплении и контроля знаний учащихся.

 

Математическая зарядка

Данная игра позволяет оперативно проверить знания большого количества учеников. Класс делится на команды по рядам, а каждый ряд подразделяется на два варианта. Учащиеся каждого варианта либо встают, либо поднимают руки, если речь идет об объекте, за который они отвечают.

Допустим, идет проверка навыков вычислений с целыми числами. Я читаю задания. Учащиеся распределяются следующим образом:

I вариант отвечает за отрицательные числа, II вариант — за положительные. Если в результате вычислений получилось отрицательное число, то все ученики первого варианта в каждом ряду должны на пальцах показать ответ. Если результат положительный, то ответ дают ученики вторых вариантов. Если в ответе получился нуль, то оба варианта не двигаются.

Кросснамберы

Кросснамбер  — один из видов числовых ребусов. Он служить одной из форм дидактической игры.

В кросснамберах предметом отгадывания являются математические задачи. Разгадывание кросснамберов я предлагаю  учащимся для проверки усвоения ими знаний по определенной теме, разнообразив тем самым виды контроля.

Разгадывание кросснамберов предпочтительнее других видов контроля тем, что в них присутствуют элементы игры, а это снимает психическое напряжение, которым, как правило, сопровождается любая проверочная работа.

Приведу пример.

 

		а	б
	в			г
д				е

 

 

 

 

По горизонтали

а) Площадь квадрата, периметр которого равен 36 см.

в)Самое маленькое четырехзначное число, в записи которого все цифры различны.

д) Наибольшее двузначное число.

е) 3/5 часа, выраженные в минутах.

По вертикали

а) Число (а) по горизонтали, уменьшенное на единицу.

б) Дюжина.

в) Делимое при известном неполном частном 16,делителе 12, остатке 6.

г) Корень уравнения 9408 : х = 517 - 489.

 

 

 

 

 

 

 

Самостоятельная деятельность как источник стимуляции

познавательного интереса

 

Формирование интереса к учению поступает из самой деятельности ученика, рождающей интеллектуальные и эмоциональные удовлетворения.

Познавательная самостоятельность, формирующаяся на базе активности,  характеризуется следующими признаками:

·         стремление  и умение самостоятельно мыслить;

·        способность ориентироваться в новой ситуации, найти свой подход к новой задаче;

·        желание  не только понять усваиваемые знания, но и способы их добывания;

·        критический  подход к суждению других;

·        независимость собственных суждений.

Развивающая функция обучения  требует не простого изложения знаний,  в определенной системе, а предполагает также учить школьников мыслить, искать и находить ответы на поставленные вопросы, добывать новые знания, опираясь на уже известные. Учащихся надо целенаправленно учить познавательной деятельности, вооружать их учебно-познавательным аппаратом. Уместно в связи с этим привести  слова М. Монтеня: “Мозг хорошо устроенный— стоит больше, чем мозг хорошо наполненный”.

Степень развитости ученика измеряется и оценивается  его способностью самостоятельно приобретать новые  знания, использовать в учебной и практической деятельности уже полученные знания.

С этой целью я предлагаю учащимся выполнять творческие домашние  задания. Например, ученикам предлагается сочинить дома задачу определенного типа, опираясь на задачи, рассмотренные в классе или имеющиеся в учебнике. Ее текст и решение учащимся необходимо аккуратно оформить. Таким образом, ребятам придется проанализировать данный материал, синтезировать свой вариант и проработать решение. Или прошу сочинить математическую сказку на применение и усвоение математических понятий (ноль, точка, дробь, прямая, луч и т.д.).

Усилить интерес школьников к математике мне помогает прием, к которому я иногда обращаюсь на уроках повторения — составление кроссвордов самими учащимися. Ребята, которые или с трудом одолевают математику, или просто не вкладывают в нее достаточно усилий, с увлечением работают на таких уроках и с удовольствием доделывают уже дома, начатый в классе кроссворд. Таким образом, они усваивают математическую терминологию, учатся формулировать вопросы, находить на них ответы.

 

 

 

 

 

 

 

Планирование лекционно–практических занятий в процессе обучения учащихся  с целью развития  их познавательного интереса

 

Опыт работы свидетельствует об эффективности применения лекционно-практической формы преподавания при изучении ряда тем курса математики. Такая организация занятий требует тщательного подбора учебного материала и конкретного планирования каждого урока.

Лекция должна охватить весь теоретический и практический материал темы. При чтении  лекции определяются крупные блоки в изложении материала, которые озаглавливаются, так что в конце лекции ученик легко просматривает ее план. Количество уроков на лекцию определяется объемом изучаемого материала, а также способностью класса воспринимать  большие дозы информации. Обычно на нее  отводятся 1—2 урока.

В конце лекции учитель сообщает учащимся о том,  что какая форма отчетности по теме  намечается, какие  вопросы выносят на зачет, объем итоговой контрольной работы.

На практических  занятиях ученики должны закрепить и углубить теоретический материал, изложенный на лекции, научиться применять его на практике, усвоить несколько алгоритмов решения типовых примеров и задач,  подготовиться к зачету и контрольной работе. На первом уроке отрабатывается материал на I уровне усвоения знаний (понял, запомнил, воспроизвел), на следующих — на II (понял, запомнил, воспроизвел, применил по образцу  в измененных условиях, где надо узнать образец) и  III (овладел знаниями на II уровне  и научился переносить их в новые условия) уровнях.

На уроках практических занятий ребята учатся отвечать на вопросы,  которые им будут предложены на зачете. Полезно проводить промежуточный контроль знаний, который позволяет своевременно  обнаружить пробелы в знании школьников и принять меры к их ликвидации. Достаточно провести 1-2 кратковременные проверочные работы.

На зачете   я осуществляю  предварительный контроль знаний, при проведении контрольной работы – окончательный. Зачет провожу письменно, по индивидуальным карточкам, которые содержат теоретические вопросы и задачи, не включенные в контрольную работу.

На обобщающем уроке проводиться обзорное повторение узловых вопросов темы и основных методов решения задач.

Урок коррекции посвящается работе по ликвидации пробелов знании учащихся, выявившихся на зачете и на контрольной работе.

 

Формирование познавательного интереса во внеурочное время

 

Основным видом внеклассной работы по математике в школе являются  математические кружки. Вызывая интерес учащихся к предмету, кружки способствуют развитию  математического кругозора,  творческих способностей учащихся, привитию навыков самостоятельной   работы и тем самым повышению качества математической подготовки  учащихся.

На занятиях кружка я готовлю опору для своей работы на уроках. В свою очередь на эти занятия переносятся с уроков наиболее тонкие и сложные моменты.

На уроках нерешенные задачи со звездочкой по изучаемой тематике, разбираю решение этих задач на занятиях кружка.

Планирование кружковых занятий носит гибкий характер: неожиданно возникший на уроке вопрос  служит темой ближайшего занятия.

Занятие математического кружка строится  по следующему  плану:

1) доклад одного из участников кружка на 5—10 мин по истории математики;

2) решение задач, в том числе повышенной трудности (*);

3) решение задач занимательного характера (о) и задач на смекалку;

 4) ознакомление участников кружка с задачами, предлагавшимися на приемных экзаменах в различные учебные заведения (к);

5) ответы на разные вопросы учащихся.

При решении задач обращаю внимание учащихся на отыскание  наиболее рациональных, оригинальных способов их решения. Так же как и при выполнении учащимися экзаменационных работ в школе и на вступительных экзамёнах в вузы или техникумы, выбор способа решения—право учащегося.

На занятиях кружка проводим разовые  мероприятия (математические вечера, викторины, олимпиады, КВН, соревнования команд и др.).  

 

 

Результативность

 

Выработанная мною система работы с учащимися по развитию познавательного интереса дает свои результаты.

1.            Доброжелательное отношение учащихся в классе.

2.            Заинтересованность учащихся в получении знаний.

3.            Умение работать с дополнительной литературой.

4.            Учащиеся могут защищать свое мнение, приводить в его защиту аргументы, доказательства.

5.            Учащиеся не боятся  задавать вопросы учителю, одноклассникам, выяснять неясное.

6.            Оценивают ответы одноклассников и вносят коррективы.

7.            Помогают одноклассникам при затруднениях, объясняют непонятое.

8.            Любят выполнять несложные поисковые и творческие задания.

9.            Любят обмениваться интересной информацией между собой.

10.        Качество знаний учащихся в зависимости от класса 40 - 70%.