ДополнительныйДидактическийМатериал2

Задача 1. Дано: АВ=12см, АМ=2см, МС=4см. На отрезке АВ случайным образом отмечается точка Х. Какова вероятность того, что точка Х попадет на отрезок:

1) АМ;  2) АС;  3) МС;  4) МВ;  5) АВ?

Задача 2. Оконная решетка состоит из клеток со стороной 20см. Какова вероятность того, что попавший в окно мяч, пролетит через решетку, не задев ее, если радиус мяча равен: а) 10см, б) 5см?

Задача 3. Оконная решетка состоит из клеток со стороной 20см. В решетку 100 раз бросили наугад один и тот же мяч. В 50 случаях он пролетел через решетку не задев ее. Оцените приближенно радиус мяча.

Задача 4.  Два друга договорились встретиться в определенном месте с 12⁰⁰ до 13⁰⁰. Пришедший ждёт другого в течение 20 минут и, если встреча не состоялась, уходит. Приход их не зависит друг от друга и равновозможен в любой момент из указанного промежутка времени. Найти вероятность того, что встреча состоится.

Задача 5. В круг вписан правильный шестиугольник. Найти вероятность того, что точка, наудачу брошенная в круг, не попадёт в правильный шестиугольник, вписанный в него.

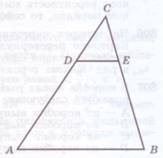Задача 6. В треугольнике АВС проведен отрезок DE, параллельный АВ. Известно, что  

Какова вероятность того, что случайным образом выбранная точка треугольника АВС окажется принадлежащей треугольнику CDE?

Задача 7. Пункты А и В находятся друг от друга на расстоянии 2,5 км. Телефонная линия, соединяющая эти пункты, оборвалась в неизвестном месте. Какова вероятность того, что точка разрыва удалена от точки А не более чем на 500 м?

Задача 8. На координатной прямой отмечены точки А(0) и В(3). На отрезке АВ наугад выбрана точка С(х). Какова вероятность того, что ?

Ответ:  6.  1/9;    7. 0,2;      8. 1,2/3=0,4