Дослідження моделі Неймана

Дослідження моделі Неймана

Модель Неймана на відміну від моделі Леонтьєва, в якій розглядається тільки один виробничий цикл, носить динамічний характер.

В моделі Неймана розглядається економіка, яка описується базисними виробничими процесами (галузями або підприємствами).

Кожен базисний процес можна зобразити в вигляді

 (), ,

де  - вектор витрат,  - вектор випуску. Зміст процесу  такий: він витрачає вектор =(a'_ij), , та випускає вектор =(x'_ij), , тобто переробляє вектор  в вектор . Ці вектори невід'ємні. Позначимо через A' та X' матриці

                                              A'=(),

                                           X'=().

Модель задається парою невід'ємних матриць A' та X'. Матриця A' називається матрицею витрат, матриця X' - матрицею випуску.

Комбінуючи базисні процеси, можна одержати нові виробничі процеси. Якщо взяти невід'ємний вектор-стовпець , , то можна описати новий виробничий процес

в якому витрати характеризує вектор , а випуск – вектор .

Нові процеси показують режим спільної роботи різних галузей. Отриманий виробничий процес позначимо (A',X') .

Вектор-стовпець  зветься вектором інтенсивностей.

Модель Неймана лінійна та замкнута. Замкнутість моделі можна показати так.

Нехай для виробництва в (t+1)-й період можна витрачати тільки ті товари, які були вироблені в попередній t-й період. Через  позначимо вектор запасів, які є до початку всього планового періоду [1,Т]. Запишемо нерівності

A' ⁽¹⁾ ≤ ,

A' ⁽²⁾ ≤ X'⁽¹⁾,

...

A' ^(t+1) ≤ X'^(t),

t=1,...,(T-1).

Позначимо також через  вектор цін

= (p_i), ,

де p_i - ціна одиниці і-го товару.

За матрицями A' та X' технологічних процесів, вектором цін  та вектором  знайти інтенсивності технологічних процесів, які максимізують вартість продукції та саму цю максимальну вартість.

Для пошуку вектора інтенсивностей = та максимального вартості необхідно використати задачу лінійного програмування. Цільову функцію можна зобразити у вигляді.

X'→max.

Обмеження будуть такі:

A'≤ ,

≥0.

Зобразимо цю задачу в розгорнутій формі

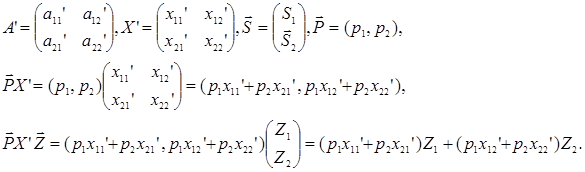
Обмеження в розгорнутій формі мають такий вигляд:

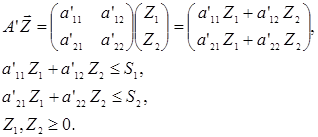
Для розв'язання задачі використати графічний метод. Побудувати координатну площину Z₁, Z₂ . Використовуючи обмеження, побудувати випуклий многокутник. Далі знайти перетин цільової функції з тією вершиною, де значення цільової функції найбільше. Координати вершини дають необхідні інтенсивності. Знайдені інтенсивності підставляють у цільову функцію для визначення максимальної вартості продукції.