Дослідження моделі Солоу

Дослідження моделі Солоу

Стан економіки в моделі Солоу задається змінними:

Y -  кінцева продукція;

L - трудові ресурси;

K - основні виробничі фонди або виробничий капітал;

І - інвестиції;

С - продукція невиробничого споживання.

Всі змінні взаємопов'язані (рис.4.1).

Назвемо нормою накопичення ρ долю кінцевої продукції, яка використовується в інвестиціях. Тоді

I=ρY,

C=(1-ρ)Y,

 0<ρ<1.

Інвестиції використовуються для відновлення фондів, які вибувають, та на їх приріст. Приймемо, що фонди вибувають із постійним коефіцієнтом вибування ОВФ μ, 0<μ<1.

Також зробимо припущення, що інвестиції у тому ж році повністю витрачаються на приріст ОВФ і на амортизацію. В дискретному варіанті цей зв'язок має вигляд

IΔt=ΔK+DΔt,

де Δt - приріст часу, ΔK - приріст капіталу, D - амортизаційні відрахування.

Перепишемо останній вираз у формі

ΔK=IΔt - DΔt,

ΔK=Δt(I-D),

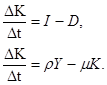
Тут амортизаційні відрахування дорівнюють D=μK.

У випадку неперервного часу аналогом останнього рівняння є

.

Якщо вважати, що приріст трудових ресурсів пропорційний наявним трудовим ресурсам (ΔL=nLΔt) , то одержуємо диференційне рівняння

де n - доля приросту трудових ресурсів.

Розв'язання рівняння дає

L=L₀e^nt,

де L₀ = L(0) - трудові ресурси на початку спостереження (для t=0).

Модель Солоу задається системою рівнянь

C=(1-ρ)Y,

Y=f(K,L),

L=L₀e^nt,

,

K(0)=K₀.

На початку спостереження основні фонди дорівнюють K₀.

Розглянемо стаціонарну траєкторію, на якій середня фондоозброєність

постійна і дорівнює своєму початковому значенню:

k(t) = const = k₀.

Позначимо стаціонарне значення фондоозброєності через . Для функції Кобба-Дугласа

Y₁= f(K₁,L₁)=F(K₁,L₁)/2=aK₁^αL₁^1-α /2,

 воно обчислюється за формулою

₁ = [ρa /( 2μ +2 n)]^{1/(1 - α)}.

Середня продуктивність праці y=.

На стаціонарній траєкторії позначимо продуктивність праці . Для функції Кобба-Дугласа можна знайти за формулою:

₁=a[ρa / (2μ +2 n)]^{α / (1 - α)} / 2.

За даними для функції Кобба-Дугласа (п.4.2) та нормою накопичення

   ρ=α, коефіцієнтом вибування фондів μ=0,03і за рік, долею приросту трудових ресурсів n=0,05і знайти значення фондоозброєності та продуктивності праці на стаціонарній траєкторії. Тут і – номер заданого варіанта.

Дослідити модель Солоу для лінійної виробничої функції (п. 4.2)

Y₂=(b₁K₂+b₂L₂)/2,

b₁=10i,  b₂=і,

 і – номер заданого варіанта.

 На основі використання рівняння

визначити математичні вирази для  та . Обчислити їх значення, підставляючи у вирази чисельні значення  . Проставити одиниці вимірювання.