Дослідження виробничих функцій

Дослідження виробничих функцій

Підсистему виробництва продукції F (рис. 4.1) можна описати за допомогою виробничої функції

X=F(K, L).

Тут змінні характеризують такі фактори: K - обсяг виробничих фондів у вартісному або натуральному вигляді (вартість або кількість обладнання), L - обсяг трудових ресурсів (кількість робітників, кількість людино-днів) , X - обсяг продукції (валової) у вартісному або натуральному вигляді.

У даному підрозділі розглядаються виробнича функція Кобба-Дугласа (для першої галузі) та лінійна виробнича функція (для другої галузі). Припускається, що ці функції неперервні та диференційовані.

Виробнича функція Кобба-Дугласа ( CDPF ) належить до найбільш відомих, широко використовуваних функцій. Функція має вигляд

X₁=aK₁ ^αL₁^1-α,

(a,α,(1-α))>0, α<1,

де (a,α) - параметри моделі.

Параметр a залежить від одиниць вимірювання змінних.

Для функції Кобба-Дугласа виконуються такі вимоги:

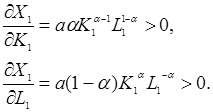
Перша похідна  характеризує граничну фондовіддачу. З виразу видно, що для цієї функції гранична фондовіддача пропорційна середній фондовіддачі та менше її

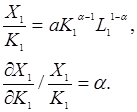
Аналогічно визначається середня та гранична продуктивність праці. Для них також виконується відношення: гранична продуктивність праці  пропорційна середній продуктивності  і менше її. Знайдемо тепер еластичність продукції за основними фондами

,

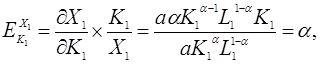та еластичність продукції за трудовими ресурсами

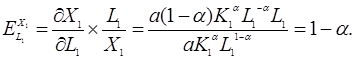
Еластичність показує, як зміниться величина Х₁, якщо величина К₁ або L₁ зміниться на 1%.

Знайдемо також граничні норми заміщення основними фондами трудових ресурсів

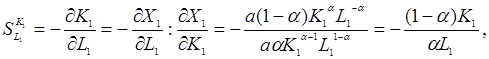
та трудовими ресурсами основних фондів

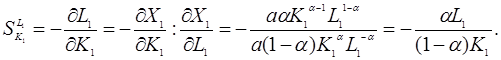
Ці норми показують, як при незмінній величині продукції можна змінити співвідношення між факторами.

За значеннями a та α заданого варіанта побудувати виробничу функцію Кобба-Дугласа для першої галузі та визначити основні характеристики

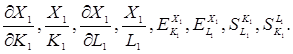
Довести однорідність першого степеня виробничої функції Кобба-Дугласа.

Для другої галузі необхідно розглянути лінійну виробничу функцію

C₂=b₁K₂+b₂L₂,

b₁=10i,  b₂=і,

де і - номер заданого варіанта. Дослідити цю функцію, обчисливши характеристики

                        , , , , .

Доказати однорідність першого степеня лінійної виробничої функції.