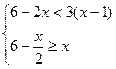Аннотация программы

 

Данная программа  курса по выбору своим содержанием может привлечь внимание учащихся 9 классов. В  9-ом классе, дети начинают чувствовать тревожность  перед  экзаменами, пытаются как-то готовиться к ним, но самостоятельно повторять и систематизировать весь материал, пройденный за последние  годы обучения, не каждому девятикласснику под силу. На занятиях этого курса  есть возможность устранить пробелы ученика по тем или иным темам. Ученик более осознанно подходит  к материалу, который изучался  в предыдущих классах, т.к. у него уже более большой опыт и богаче багаж знаний. Учитель помогает выявить  слабые места ученика, оказывает помощь при систематизации материала, готовит правильно оформлять экзаменационную работу.

 Стоит отметить, что навыки решения математических задач совершенно необходимы всякому ученику, желающему хорошо подготовиться и успешно сдать экзамены по алгебре, добиться значимых результатов при участии в математических конкурсах и олимпиадах.

Исторические моменты в рамках курса будут особо привлекательны для учеников с гуманитарными наклонностями. Не исключено, что данный курс поможет ученику найти свое призвание в профессиональной деятельности, требующей использования точных наук или, по крайней мере, приобрести вне профессиональное увлечение, пусть и не на всю оставшуюся жизнь. Поэтому его можно использовать как в рамках подготовки учащихся, так и для профильных классов различного направления.

 

Пояснительная записка

В 2018-2019 учебном году начат эксперимент по созданию системы подготовки учащихся основной школы, которая, в частности, предполагает изучение школьниками предметных курсов по выбору. Подходы к созданию таких курсов могут быть различны.

Особенность принятого подхода курса по выбору «Математика: подготовка ГИА» состоит в том, что для занятий по математике предлагаются небольшие фрагменты, рассчитанные на 2-3 урока, относящиеся к различным разделам школьной математики.

Каждое занятие, а также все они в целом направлены на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и  методами, расширить представление об изучаемом в основном курсе материале, а главное, рассмотреть интересные задачи.

 Этот курс предлагает учащимся знакомство с математикой как с общекультурной ценностью, выработкой понимания ими того, что математика является инструментом познания окружающего мира и самого себя.

Если в изучении предметов естественнонаучного цикла очень важное место занимает эксперимент и именно в процессе эксперимента и обсуждения его организации и результатов формируются и развиваются интересы ученика к данному предмету, то в математике эквивалентом эксперимента является решение задач. Собственно весь курс математики может быть построен и, как правило, строится на решении различных по степени важности и трудности задач.

Курс по  выбору «Математика: подготовка к ГИА» рассчитан на 34 часа для работы с учащимися 9 классов и предусматривает повторное  рассмотрение теоретического материала по математике, поэтому имеет большое общеобразовательное значение, способствует развитию логического мышления, намечает и использует целый ряд межпредметных связей (прежде всего с историей).

 

Цель данного курса: оказание индивидуальной  и систематической помощи девятикласснику при повторении алгебры и подготовке к экзаменам.

 

   Задачи курса:

- обучающие: (формирование познавательных и логических УУД) подготовить учащихся к экзаменам.

- развивающие: (формирование регулятивных УУД) развивать умение пользоваться полученной информацией; формировать коммуникативную компетенцию учащихся, а также контроль и оценку процесса и результатов деятельности.

- воспитательные: (формирование коммуникативных и личностных УУД) формировать умение слушать и вступать в диалог; воспитывать ответственность и аккуратность; участвовать в коллективном обсуждении при этом учиться умению осознанно и правильно строить речевое высказывание в устной и письменной форме.

Функции  курса:

·            ориентация на совершенствование навыков познавательной, организационной деятельности;

·            компенсация недостатков ЗУН по математике.

                                                             

Методы и формы обучения

Методы и формы обучения определяются требованиями обучения, с  учетом  индивидуальных и возрастных особенностей учащихся, развития и саморазвития личности. В связи с этим основные приоритеты методики изучения  курса:

·            обучение через опыт и сотрудничество;

·            учет индивидуальных особенностей и потребностей учащихся;

·            интерактивность (работа в малых группах, ролевые игры, тренинги, вне занятий - метод проектов);

·            личностно-деятельностный и субъект–субъективный подход (большее внимание к личности учащегося, а не целям учителя, равноправное их взаимодействие).

Для работы с учащимися безусловно применимы такие формы работы, как лекция и семинар. Помимо этих традиционных форм рекомендуется использовать также дискуссии, выступления с докладами, содержащими отчет о выполнении индивидуального или группового домашнего задания или с содокладами, дополняющими лекцию учителя. Возможны различные формы творческой работы учащихся, как например, «защита решения», отчет по результатам «поисковой» работы на образовательных сайтах в Интернете по указанной теме. Таким образом, данный курс не исключает возможности проектной деятельности учащихся во внеурочное время. Итогом такой деятельности могут быть творческие работы.

     Предлагаемый курс является развитием системы ранее приобретенных программных знаний, его цель - создать целостное представление о теме и значительно расширить спектр задач, посильных для учащихся. Все свойства, входящие в курс, и их доказательства не вызовут трудности у учащихся, т.к. не содержат громоздких выкладок, а каждое предыдущее готовит последующее. При направляющей роли учителя школьники могут самостоятельно сформулировать новые для них свойства и даже доказать их. Все должно располагать к самостоятельному поиску и повышать интерес к изучению предмета. Представляя учащимся возможность осмыслить свойства и их доказательства, учитель развивает геометрическую интуицию, без которой немыслимо творчество. "Интуиция гения более надежна, чем дедуктивное доказательство посредственности" (Клайн).

Таким образом, программа применима для различных групп школьников, в том числе, не имеющих хорошей подготовки. В этом случае, учитель может сузить требования и предложить в качестве домашних заданий создание творческих работ, при этом у детей развивается интуитивно-ассоциативное мышление, что несомненно, поможет им при выполнении заданий ГИА.

Основная функция учителя в данном курсе состоит в «сопровождении» учащегося в его познавательной деятельности, коррекции ранее полученных учащимися ЗУН.

 

 

 

 

 

 

 

 

Программа содержит шесть блоков, связанные единой идеей, в то же время они построены по модульному принципу. Учитель, в зависимости от уровня математической подготовки класса, может использовать все разделы блока или любой из них.

            Первый блок систематизирует ранее полученные знания о числах и действиях с числами. На блок отводится 4 часа вместе с решением задач на проценты.

o    Натуральные числа. Делимость натуральных чисел

o    Дроби. Все действия с дробями

o    Отношения. Пропорции. Проценты.

o    Действия чисел с разными знаками. Сравнение чисел

            На второй блок отводится 7 часов, их цель - вывод формул, эффективно используемых при решении многих других задач. Их полезно свести в таблицу и использовать в дальнейшем, как справочный материал. У школьников появится некоторый минимум знаний, без которых они не могут продвинуться дальше в решении даже простейших задач.

o    Иррациональные числа. Действия с иррациональными числами

o    Степень с натуральным показателем

o    Квадратный корень. Свойства квадратных корней и их применение в вычислениях

o    Алгебраические выражения и их преобразования

o    Многочлены, разложение многочленов на множители

o    Алгебраические дроби, действия с алгебраическими дробями

o    Рациональные выражения и их преобразования

            В зависимости от уровня подготовки класса, на доказательство основных соотношений может быть отведено 2 или 3 занятия, на оставшихся школьники учатся применять полученные знания к практике решения задач.

 Третий блок включает в себя задачи на  решение уравнений и систем уравнений,  также

рассматривает функции.

o    Уравнения. Квадратные уравнения

o    Рациональные уравнения

o    Системы уравнений

o    Графический способ решения уравнений

o    Функции. Способы задания функций. Область определения и область значений функции

o    Графики функции

Четвертый блок посвящен решению задач, решаемых с помощью числовых последовательностей.

o    Последовательности.

o    Арифметическая прогрессия.

o    Геометрическая прогрессия.

Пятый блок посвящен решению задач по планиметрии, на этот блок отводится 5 часов.                                                                                                              

o    Геометрические фигуры и их свойства. Измерение геометрических величин.

o    Треугольник

o    Многоугольники.

o    Окружность и круг.

o    Измерение геометрических величин.

o    Векторы на плоскости.

 

Шестой блок посвящен  элементам логики, комбинаторики, статистики и теории вероятностей.

o    Описательная статистика.

o    Вероятность.

o    Комбинаторика

 

Итоговым занятием планируется провести зачет.

Таким образом, на изучение шести  блоков отводится 34 часов, из них 5 часов - на определение успешности усвоения материала.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ  УЧАЩИХСЯ 9 КЛАССА

 

Выпускник научится / получит возможность узнать:

• значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе;
• значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;  вероятностный характер различных процессов окружающего мира;
• существо понятия алгоритма; примеры алгоритмов;
• как используются математические формулы, уравнения; примеры их применения при решении  математических и практических задач;
• как математически определённые функции  могут описывать реальные зависимости; приводить примеры такого описания;
• как  потребности практики  привели математическую науку к необходимости расширения понятия числа;
• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

·                выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

·                моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

·                описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;

интерпретации графиков реальных зависимостей между величинами

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ В ОСВОЕНИИ ШКОЛЬНИКАМИ  УУД ПО ЗАВЕРШЕНИИ ОБУЧЕНИЯ
Личностные	Специально-предметные УУД	Метапредметные УУД
		Регулятивные	Познавательные	Коммуникативные
-положительное отношение к урокам математики; -умение признавать собственные ошибки; -формирование ценностных ориентаций (саморегуляция, стимулирование, достижение и др.); -формирование математической компетентности В сфере личностных ууд у выпускников будут сформированы внутренняя позиция обучающегося, адекватная мотивация учебной деятельности, включая учебные и познавательные мотивы, ориентация на моральные нормы и их выполнение.	--выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; --составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные; --выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять тождественные преобразования рациональных выражений; --применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни; --решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения; --решать текстовые задачи алгебраическим методом,  проводить отбор решений, исходя из формулировки задачи; --определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства; --находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей; --определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств; --описывать свойства изученных функций, строить их графики.	-отслеживать цель учебной деятельности (с опорой на маршрутные листы) и внеучебной (с опорой на развороты проектной деятельности); -учитывать ориентиры, данные учителем, при освоении нового учебного материала; -проверять результаты вычислений; -адекватно воспринимать указания на ошибки и исправлять найденные ошибки. -оценивать собственные успехи в вычислительной деятельности; -планировать шаги по устранению пробелов (знание состава чисел). В сфере регулятивных ууд выпускники смогут овладеть всеми типами уч.действ.направленных на организацию своей работы в ОУ и вне его, включая способность принимать и сохранять учебную цель и задачу, планировать ее реализацию, контролировать и оценивать свои действия, вносить соответствующие коррективы и их выполнение	--анализировать условие задачи (выделять числовые данные и цель — что известно, что требуется найти); -сопоставлять схемы и условия текстовых задач; -устанавливать закономерности и использовать их при выполнении заданий; -осуществлять синтез числового выражения, условия текстовой задачи (восстановление условия по рисунку, схеме, краткой записи); -сравнивать и классифицировать изображенные предметы и геометрические фигуры по заданным критериям; -понимать информацию, представленную в виде текста, схемы, таблицы. -видеть аналогии и использовать их при освоении приемов вычислений; -конструировать геометрические фигуры из заданных частей; достраивать часть до заданной геометрической фигуры; мысленно делить геометрическую фигуру на части; -сопоставлять информацию, представленную в разных видах; -выбирать задание из предложенных, основываясь на своих интересах. В сфере познавательных УУД выпускники научатся воспринимать и анализировать сообщения и важнейшие их компоненты-тексты, использовать знаково-символические средства, в том числе овладевают действием моделирования, а также широким спектром логических  действий и операций, включая общие приемы решения задач	--сотрудничать с товарищами при выполнении заданий: устанавливать и соблюдать очерёдность действий, сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках; -задавать вопросы с целью получения нужной информации; -организовывать взаимопроверку выполненной работы; -высказывать свое мнение при обсуждении задания В сфере коммуникативных ууд выпускники приобретут умения учитывать позицию собеседника(партнерства), организовывать и осуществлять сотрудничество и кооперацию с учителем и сверстниками, адекватно воспринимать и передавать информацию, отображать предметное содержание и условия деятельности в сообщениях, важнейшими компонентами которых являются тексты заданий.

 

 

 

 

 

 

 

 

 

 

 

 

 

Общая характеристика курса

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика, алгебра, геометрия, элементы комбинаторики теории вероятностей, статистики и логики.  В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.

Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как  языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

Геометрия – один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит  вклад в развитие логического мышления, в формирование понятия доказательства.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Организация и проведение аттестации учеников

 

       Основными результатами освоения содержания элективного курса учащимися может быть определенный набор общеучебных умений, а также приобретение опыта проектной внеурочной деятельности, содержательно связанной с предметным полем – математикой. При этом должна использоваться преимущественно качественная оценка выполнения заданий, хотя возможно и итоговое тестирование учащихся.

 

Начинается курс с ознакомительной вводной лекции. Следующее за ней занятие посвящается входному тестированию, цели которого:

Ø Составить представление учителя об уровне базовых знаний учащихся, выбравших курс.

Ø Коррекция в связи с этим уровня подачи материала по данному курсу.

При прослушивании блоков лекционного материала и проведения семинара, закрепляющего знания учащихся, предусматривается индивидуальное или групповое домашнее задание, содержащее элементы исследовательской работы, задачи для самостоятельного решения. Защита решений и результатов исследований проводится на выделенном для этого занятии и оценивается по пятибалльной системе или системе «зачет-незачет», в зависимости от уровня подготовленности группы.

Начиная с 5 – 7 занятия учащиеся сами выбирают форму итоговой аттестации:

Ø         Защита проекта.

Ø         Итоговая контрольная работа.

 

 

 

 

Методические рекомендации по реализации программы.
Основным дидактическим средством для предлагаемого курса являются тексты рассматриваемых типов задач, которые могут быть выбраны из разнообразных сборников, различных вариантов ЕГЭ или составлены самим учителем.

Курс обеспечен раздаточным материалом, подготовленным на основе прилагаемого ниже списка литературы.

Для более эффективной работы учащихся целесообразно в качестве дидактических средств использовать плакаты с опорными конспектами или медиа - ресурсы.

 

Содержание курса и распределение часов по темам

Данный элективный курс рассчитан на 34  тематических занятия.

 

 

 

Планирование занятий курса по выбору по математике в 9 классе

«Математика: подготовка к ГИА»

№	Тема
	МАТЕМАТИКА
	Первый блок
1.	Натуральные числа. Делимость натуральных чисел
2.	Дроби. Все действия с дробями
3.	Отношения. Пропорции. Проценты.
4.	Действия чисел с разными знаками. Сравнение чисел
	Второй блок
5.	Иррациональные числа. Действия с иррациональными числами
6.	Степень с натуральным показателем
7.	Квадратный корень. Свойства квадратных корней и их применение в вычислениях
8.	Алгебраические выражения и их преобразования
9.	Многочлены, разложение многочленов на множители
10.	Алгебраические дроби, действия с алгебраическими дробями
11.	Рациональные выражения и их преобразования
	Третий блок
12.	Уравнения. Квадратные уравнения
13.	Рациональные уравнения
14.	Системы уравнений
15.	Графический способ решения уравнений
16.	Функции. Способы задания функций. Область определения и область значений функции
17.	Графики функции
	Четвертый блок  (3часа)
18.	Последовательности.
19.	Арифметическая прогрессия
20.	Геометрическая прогрессия
	ГЕОМЕТРИЯ (ПЛАНИМЕТРИЯ)
	Пятый блок (6 часов)
21.	Геометрические фигуры и их свойства. Измерение геометрических величин
22.	Треугольник
23.	Многоугольники
24.	Окружность и круг
25.	Измерение геометрических величин
26.	Векторы на плоскости
	Шестой блок
	РЕАЛЬНАЯ МАТЕМАТИКА
	Статистика и теория вероятностей
27.	Описательная статистика
28.	Вероятность
29.	Комбинаторика
30-33	Решение тестовых заданий. Подготовка к ГИА
34	Резерв

 

 

                                                               ОСНОВНОЕ СОДЕРЖАНИЕ
                                                                                    (34часа)                                          

                Арифметика

Натуральные числа.  Степень с натуральным показателем.

Рациональные числа. Модуль (абсолютная величина) числа. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Степень с целым показателем.

Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий: переместительный, сочетательный, распределительный.

Действительные числа. Квадратный корень из числа. Корень третьей степени. Понятие о корне n-ой степени из числа1. Нахождение приближенного значения корня с помощью калькулятора. Запись корней с помощью степени с дробным показателем.

Понятие об иррациональном числе. Иррациональность числа. Десятичные приближения иррациональных чисел.

Действительные числа как бесконечные десятичные дроби. Сравнение действительных чисел, арифметические действия над ними.

Этапы развития представлений о числе.

Измерения, приближения, оценки . Размеры объектов окружающего нас мира (от элементарных частиц до Вселенной), длительность процессов в окружающем нас мире.

Представление зависимости между величинами в виде формул.

Выделение множителя – степени десяти в записи числа.

Алгебра 

Алгебраические дроби. Арифметические операции над алгебраическими дробями. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных. Равенство буквенных выражений. Тождество, доказательство тождеств. Преобразования выражений.

Свойства степеней с целым показателем. Многочлены. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формула суммы кубов и разности кубов. Разложение многочлена на множители. Квадратный трехчлен. Выделение полного квадрата в квадратном трехчлене. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Многочлены с одной переменной. Степень многочлена. Корень многочлена.

         Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями.

Рациональные выражения и их преобразования. Свойства квадратных корней и их применение в вычислениях.

Уравнения и неравенства. Уравнение с одной переменной. Корень уравнения. Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения, Решение рациональных уравнений. Примеры решения уравнений высших степеней; методы замены переменной, разложения на множители.

Уравнение с двумя переменными; решение уравнения с двумя переменными. Система уравнений; решение системы. Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением. Уравнение с несколькими переменными. Примеры решения нелинейных систем. Примеры решения уравнений в целых числах.

Неравенство с одной переменной. Решение неравенства. Линейные неравенства с одной переменной и их системы. Квадратные неравенства. Примеры решения дробно-линейных неравенств.

Числовые неравенства и их свойства. Доказательство числовых и алгебраических неравенств.

Переход от словесной формулировки соотношений между величинами алгебраической.       Решение текстовых задач алгебраическим способом.

 

Числовые последовательности. Понятие последовательности. Арифметическая и геометрическая прогрессии. Формулы общего члена арифметической и геометрической прогрессий, суммы первых нескольких членов арифметической и геометрической прогрессий.

Числовые функции. Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства. Чтение графиков функций.

Функции, описывающие прямую и обратную пропорциональную зависимости, их графики. Линейная функция, ее график, геометрический смысл коэффициентов. Гипербола. Квадратичная функция, ее график, парабола. Координаты вершины параболы, ось симметрии. Степенные функции с натуральным показателем, их графики. Графики функций: корень квадратный, корень кубический, модуль. Использование графиков функций для решения уравнений и систем.

Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост; числовые функции, описывающие эти процессы.

Параллельный перенос графиков вдоль осей координат и симметрия относительно осей.

Координаты. Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Числовые промежутки: интервал, отрезок, луч. Формула расстояния между точками координатной прямой.

Декартовы координаты на плоскости; координаты точки. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых. Уравнение окружности с центром в начале координат и в любой заданной точке.

Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем.

 

Геометрия

Начальные понятия и теоремы геометрии .

Возникновение геометрии из практики.

Геометрические фигуры и тела. Равенство в геометрии.

Точка, прямая и плоскость.

Понятие о геометрическом месте точек.

Расстояние. Отрезок, луч. Ломаная.

Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства.

Параллельные и пересекающиеся прямые. Перпендикулярность прямых. Теоремы о параллельности и перпендикулярности прямых. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой.

Многоугольники.

Окружность и круг.

Наглядные представления о пространственных телах: кубе, параллелепипеде, призме, пирамиде, шаре, сфере, конусе, цилиндре. Примеры сечений. Примеры разверток.

Треугольник. Прямоугольные, остроугольные, и тупоугольные треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника.

Признаки равенства треугольников. Неравенство треугольника. Сумма углов треугольника. Внешние углы треугольника. Зависимость между величинам сторон и углов треугольника.

Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников.

Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.

Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. Окружность Эйлера.

Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция.

Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Вписанные и описанные многоугольники. Правильные многоугольники.

Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Сектор, сегмент. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.

Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.

Измерение геометрических величин. Длина отрезка. Длина ломаной, периметр многоугольника.

Расстояние от точки до прямой. Расстояние между параллельными прямыми. Длина окружности, число p; длина дуги. Величина угла. Градусная мера угла, соответствие между величиной угла и длиной дуги окружности.

Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.

Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона. Площадь четырехугольника.

Площадь круга и площадь сектора.

Связь между площадями подобных фигур.

Векторы.

Длина (модуль) вектора. Координаты вектора. Равенство векторов. Операции над векторами: умножение на число, сложение, разложение, скалярное произведение. Угол между векторами.

Элементы логики, комбинаторики,
статистики и теории вероятностей

Доказательство. Определения, доказательства, аксиомы и теоремы; следствия. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы.

Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Эвклида и его история.

Множества и комбинаторика. Множество. Элемент множества, подмножество. Объединение и пересечение множеств. Диаграммы Эйлера.

Примеры решения комбинаторных задач: перебор вариантов, правило умножения.

Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки.

Понятие и примеры случайных событий.

Вероятность. Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.

 

 

Итоговая контрольная работа.

В зависимости от уровня подготовленности учащихся и степени совершенства выполненных проектов можно для хорошо подготовленных учащихся проводить защиту проектов по мере изучения тем, а в конце курса итоговую контрольную работу.

Если учащиеся имеют ограниченные возможности, слабые «математические» способности, то  можно ограничиться защитой проектов.

 

 

 

Комбинаторные задачи

Рассмотрим задачи математической науки, которая называется комбинаторикой.

Комбинаторика - это раздел математики, отвечающий на вопросы сколькими способами можно выбрать элементы определенного множества, если выборка удовлетворяет некоторым свойствам.

Или, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Эти методы носят следующие названия: метод перебора, дерево выбора (дерево возможных вариантов), и правило умножения.

Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?

Решение. Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Однако существует единый подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.

Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения можно построить специальную схему.

Эта схема действительно похожа на дерево, правда, "вверх ногами" и без ствола. Знак “*” изображает корень дерева, ветви дерева – различные варианты решения. Чтобы получить двузначное число, надо сначала выбрать первую его цифру, а для нее есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7.

Теперь надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры проведено по три отрезка, на концах которых снова записано 1, 4 или 7. Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

Дополнительная подзадача: Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7, если цифры десятков и единиц не повторяются? (Ответ: 6)

Задача 2. Сколько трехзначных чисел можно составить, используя цифры 3 и 5?

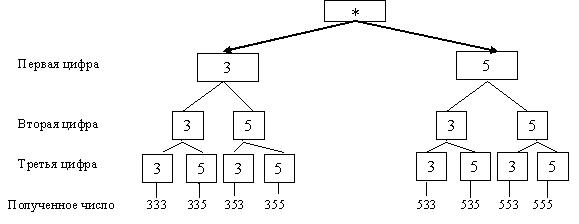
Ответ: 8

Задача 3. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

Перебор упрощается, если ввести удобные условные обозначения. Например, если в задаче речь идет о расположении в ряд нескольких красных и зеленых шаров, то не надо рисовать эти шары или писать полностью их цвета. Можно ограничиться только первыми буквами цвета этих шаров - К и 3. Такую замену предметов их условными обозначениями называют кодированием.

Обозначим города их первыми буквами. Тогда код каждого маршрута будет состоять из трех букв: В, Р и Ф, каждая из которых должна быть использована только один раз, например, ВФР или ФРВ.

Варианты путешествия получаются следующие: ВРФ, ВФР, РВФ, РФВ, ФВР, ФРВ, что хорошо видно из дерева вариантов.

Путешествие можно начинать в любом из трех городов. Если первой посетить Венецию, то затем можно поехать в Рим или во Флоренцию. Если вторым посетить Рим, то третьей будет Флоренция, если второй будет Флоренция, то третьим будет Рим. Это первые два варианта путешествия.

Таким образом, всего существует 6 вариантов путешествия.

Задача 4. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Дадим каждому из приятелей номер – от 1 до 8. Тогда каждое рукопожатие можно закодировать двузначным числом. Например, 47 – это рукопожатие между приятелями с номерами 4 и 7.

Ясно, что среди кодов рукопожатий у нас не появится, например, 33 – это означало бы, что один из друзей пожал руку сам себе. Кроме того, такие коды, как, например, числа 68 и 86, означают одно и то же рукопожатие, а значит, учитывать надо только одно из них.

Договоримся, что из чисел, кодирующих одно и то же рукопожатие, мы всегда будем учитывать меньшее. Поэтому из чисел 68 и 86 надо выбрать 68.

Коды рукопожатий естественно выписывать в порядке возрастания. Для подсчета их удобно расположить треугольником.

Число кодов равно: 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28. Таким образом, всего было сделано 28 рукопожатий.

Задача 5. Служитель зоопарка должен дать зайцу два различных овоща. Сколькими различными способами он может это сделать, если у него есть морковь, свекла и капуста?

В итоге получаем 6 вариантов при учете, что мы делаем различие между МС и СМ и другими аналогичными парами. Но, если смотреть на то, что три из них эквивалентны трем другим парам (МС – СМ, МК – КМ, СК – КС), то получаем, что различных вариантов только три.

Задача 6. В спортивном лагере “Орленок” собирались проводить первенство по футболу. Незадолго до начала соревнований к начальнику лагеря пришел вожатый, который должен был судить встречи, и сказал: “Иван Владимирович! У нас на складе есть трусы и майки только трех цветов: белого, черного и синего. А команд у нас восемь. Как быть?” – “Да совсем просто, Леня! – ответил тот.– Ведь необязательно, чтобы майки и трусы были одного цвета. Можно одну команду одеть в синие майки и белые трусы, а другую – в белые майки и синие трусы. Вот игроки и увидят, где свой, а где соперник”. – “А хватит ли таких комбинаций на восемь команд?” – "Не только хватит, еще одна останется про запас".

Посмотрим на табличку.

Здесь первая буква показывает цвет майки, а вторая – цвет трусов. Можно видеть, что получилось девять различных комбинаций, так что все в порядке.

Составляя такие таблицы, можно найти число комбинаций и в случае, когда, например, есть майки различных пяти цветов, а трусы – четырех цветов. В этом случае в таблице будет пять строк и четыре столбца, а потому общее число комбинаций окажется

равным 4 * 5, то есть 20. Вообще, если имеются майки т различных цветов и трусы п различных цветов, то общее число комбинаций для составления формы играющих команд равно т *  п.

Полученный результат верен и тогда, когда комбинируются не майки с трусами, а, например, ложки с вилками. Он гласит:

Если надо выбрать пару вещей, причем первую вещь можно выбрать m способами, а вторую n способами, то пару можно выбрать m* n способами.

Бывает, что надо выбрать не две, а три или четыре вещи. Тогда число комбинаций ищут похожим образом: смотрят, сколькими способами можно выбрать каждую вещь, и перемножают полученные числа. Поэтому правило называют правилом произведения (или правило умножения).

Вернемся теперь к первой задаче о комбинациях, которую мы решали, к задаче о выборе формы для футболистов. Чтобы решить ее, была составлена таблица из трех строк и трех столбцов. Но если бы надо было еще выбирать цвет бутс, то пришлось бы составлять не одну, а несколько таблиц – по одной для каждого цвета бутс. Поэтому, в этом случае, удобнее было бы изображать разные варианты выбора с помощью дерева возможных вариантов.

Такие деревья мысленно воображают себе шахматисты, выбирая наилучший ход в трудной позиции. Каждая полоса соответствует полуходу (ходу за белых или за черных). И думает шахматист: если я пойду так, а противник ответит так, а потом я пойду так, а он ответит так, то какой же ход мне выбрать? Мы уже видели, что с увеличением числа полос количество возможностей очень быстро возрастает. Поэтому пройти по всем веточкам дерева расчета бывает очень трудно, а иногда даже невозможно.

Со всем этим столкнулись ученые, составлявшие шахматные программы для вычислительных машин. Им удалось справиться со всеми трудностями, и теперь уже некоторые вычислительные машины играют сильнее мастера.

Задача 7. В том же спортивном лагере повар умел готовить четыре различных супа: щи, борщ, молочный суп с лапшой и фасолевый суп. Мясных блюд он умел делать пять: котлеты, зразы, шницели, биточки и суфле. При этом, к каждому мясному блюду он умел делать три гарнира: гречневую кашу, макароны и картофельное пюре. А на сладкое он готовил тоже три блюда: компот, кисель или печеные яблоки. Сколько различных обедов умел готовить этот повар?

Если вы разобрались в правиле произведения, то ответ найдете сразу: повар умел готовить 4 * 5 * 3 * 3, то есть 180 различных обедов. Так что он мог ни разу не повторить обеда за три смены.

Задача 8. В одном городе были трехзначные велосипедные номера. Но велосипедисты попросили, чтобы в этих номерах не встречались цифры 0 и 8, потому что первая из них похожа на вытянутое колесо, ну, а что значит для велосипедиста восьмерка колеса, знает каждый. Хватит ли им номеров, если в этом городе велосипеды имеют 710 человек?

Чтобы решить эту задачу, будем составлять номера следующим образом. Сначала выберем цифру сотен. Так как цифры 0 и 8 запретны, то остается 8 различных возможностей, а именно 1, 2, 3, 4, 5, 6, 7, 9. Столько же возможностей и для выбора цифры десятков, и для выбора цифры единиц. А тогда по правилу произведения получаем, что общее число велосипедных номеров,  которые  можно  было  выдать  в  этом городе, равно 8 * 8 * 8, то есть 512. Так что на всех обладателей велосипедов номеров не хватило. Поэтому пришлось велосипедистам смягчить свои пожелания. Они согласились на цифру 0. После этого число номеров стало равно 9 * 9 * 9, то есть 729, и их хватило на всех.

Задача 9. Катание на карусели. Ребята Андрей, Боря, Витя, Гриша, Дима и Женя решили покататься на карусели. На ней было 6 сидений. Одно изображало льва, другое - тигра, третье - слона, четвертое - оленя, пятое - медведя и шестое - жирафа. Ребята заспорили, кому на какого зверя садиться. Поэтому они решили перепробовать все способы. Сколько раз пришлось им прокатиться на карусели?

Чтобы решить эту задачу, будем сажать ребят в порядке алфавита. Первым выбирал Андрей. Он мог сесть на любого из шести зверей, так что у него было 6 возможностей выбора. Но когда он занял свое место. Боре остались лишь 5 возможностей – одно место было уже занято. Точно так же Вите остались 4 варианта выбора, Грише – 3, Диме – 2, а когда садился на карусель Женя, ему оставалось только одно свободное место.

А теперь по правилу произведения находим, сколькими способами могли сесть за карусель ребята: 6 * 5 * 4 * 3 * 2 * 1. В математике такое произведение обозначают 6! и называют “6-факториал”. Перемножая эти числа, получаем ответ 720. Так что, если даже они катались в день по 20 раз, то им пришлось бы больше месяца ходить каждый день в парк.

Если бы и ребят, и мест на карусели было не 6, а 8, то пришлось бы перемножать числа от 1 до 8. Это произведение равно уже 40 320. А для десятиместной карусели и десяти ребят получается более 3 миллионов вариантов.

В другой раз на ту же карусель пришли только четверо ребят: Андрей, Боря, Витя и Гриша. Узнаем, сколькими способами могут они сесть на нее. По правилу произведения надо перемножить лишь четыре числа: 6, 5, 4 и 3. Получится ответ 360. А если бы трое ребят решили перебрать все способы катания на десятиместной карусели, то умножать пришлось бы только три числа: 10, 9 и 8.

Задача 10. Хоккейная комбинация. На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. Сколько всего  возможных вариантов передачи шайбы может быть?

Есть фиксированные места, поэтому схема выглядит так:  №1, _ , _ , _ , №5. Тогда рассуждаем: Игроку №2 осталось 3 варианта выбора позиции (2 позиции заняты игроками №1 и №5), игроку №3 остались 2 варианта,  игроку №4 остался 1 вариант. Найдем все возможные передачи шайбы: 3 * 2 * 1 = 6.   Ответ: 6

 

 

 

 

Диагностический тест

                    Действия с обыкновенными дробями.

Вариант 1.

1.     Какая запись правильная, если из дроби  вычесть дробь ?

а) += ;               в) -=;

б)  -=;               г) свой ответ.

2.     Сумма чисел  и  равна:

а) ;               б) ;              в);              г) свой ответ.

3.     Разность чисел  и  равна:

а) ;               б) ;              в);              г) свой ответ.

4.     Значение выражения + равно:

а) ;               б) ;              в);              г) свой ответ.

5.     Значение выражения  -  равно:

а) ;               б) ;           в);              г) свой ответ.

6.   Корень уравнения х - =равен:

а) ;               б) ;           в);              г) свой ответ.

       7.   Укажите целую часть в смешанном числе .

а) 3;               б) ;           в) 7;              г) свой ответ.

       8.  Укажите дробную часть в смешанном числе .

а) 12;               б) 5;           в) ;              г) свой ответ.

 

9.   Сколько натуральных чисел заключено между числами  и ?

а) ;               б) 10;              в) 9;              г) свой ответ.

10.  Число 5 можно представить в виде дроби со знаменателем 20 так:

а) ;               б);              в) ;              г) свой ответ.

11.  Частное чисел 7 и 5 записывается в виде смешанного числа так:

а) ;               б);              в) ;              г) свой ответ.

 

 

 

    

                       Диагностический тест

                                      Проценты.

Вариант 1 .

1.     Какое из равенств верное?

а)  1%=0,01;                        в)  1%=100;

б)  1%=0,100;                      г) свой ответ.

2.     Как записать десятичной дробью 5%?

а)  0,0г5;                        в)  5,0;

б)  0,5;                          г) свой ответ.

3.     Как записать десятичной дробью 120%?

а)  1,2;                            в)  12,0;

б)  0,12;                          г) свой ответ.

4.     Как записать 0,2 с помощью процентов?

а)  0,02%;                            в)  20%;

б)  2%;                                г) свой ответ.

5.     Как записать 0,06 с помощью процентов?

а)  60%;                              в)  0,06%;

б)  6%;                                г) свой ответ.

6.     Найдите 1% от 200.

а)  20 000;                            в)  200;

б)  2;                                     г) свой ответ.

7.     Найдите 1% от 17.

а)  0,017;                            в)  0,17;

б)  1,7;                               г) свой ответ.

8.     Найдите 3% от 60.

а)  0,18;                            в)  180;

б)  1,8;                               г) свой ответ.

9.     Найдите 25% от 360.

а)  90;                             в)  120;

б)  9;                               г) свой ответ.

10. Из овса получается 40% муки. Сколько получится муки из 26,5 т овса?

а)  106 т;                                в)  1,06 т;

б)  10,6 т;                               г) свой ответ.

11. Чему равно число, 1% которого равен  96?

а)  9600;                                в)  0,96;

б)  960;                                г) свой ответ.

     12.Чему равно число, 3% которого равны 63?

а)  189;                                в)  210;

б)  2100;                               г) свой ответ.

13. Если 8% пути составляют 48 км, то чему равен весь путь?

а)  60 км;                                   в)  600 км;

б)  6000 км;                               г) свой ответ.

 

 

 

 

 

 

ТЕСТ

                 Делимость чисел. Признаки делимости.

Вариант 1

1.     Какие из данных утверждений не верны:

1)   3 делитель 26;        2)   37 делитель 814;

3)   23 делитель 943;   4)   67 делитель 3350;

5)   4 делитель 4;         6)   0 делитель 5.

а)   1 и 6;     б)  1, 4 и 6;     в)  1, 5 и 6;     г)  свой ответ.

2.     Какие из данных утверждений верны?

1)    33 кратно 11;        2)   565 кратно 15;

3)   67 кратно 67;         4)   672 кратно 1;

5)   17 кратно 0;           6)   45 кратно 2.

а)   1, 3, 4;     б)  1, 2, 3;     в)  1, 2, 3, 4;     г)  свой ответ.

3.     Какое из данных выражений принимает только нечетные значения, если a и b ­– нечетные натуральные числа и a>b?

а)   a+b;     б)  a-b;     в)  a·b;     г)  2a-2b.

4.     Какие из данных сумм кратны 5:

            1)  7316+97564;             2)  4523+7415;

            3)  678+991+31;             4)  230+179.

а)   1 и 3;     б)  1 и 4;     в)  1;     г)  таких нет.

5.     Какие из данных чисел не кратны 3:

            1)  1706;                  2)  12364;            3)  40215;

            4)  131421;              5)  18279.

а)   1 и 5;     б)  1 и 2;     в)  1 и 4;     г)  свой ответ.

6.     Найдите остаток от деления числа 78567 на 5.

а)   1;          б)  2;          в)  3;          г)  свой ответ.

7.     Разложите на простые множители число 420.

а)   420 = 2·2·3·5·7;     б) 420 = 1·2·2·3·5·7;     в) 420 = 4·3·5·7;   

г)  свой ответ.

8.     У каких из предложенных пар чисел НОД равен 4:

            1)  24 и 20;                  2)  24 и 30;            3)  24 и 32;

            4)  18 и 32;                  5)  4 и 16.

а)   2, 3, 5;          б)  1, 5;          в)  1, 3, 5;          г)  у всех.

9.     У каких из предложенных пар чисел НОК равно 24:

            1)  24 и 2;                  2)  18 и 12;            3)  3 и 8;

            4)  12 и 32;                 5)  4 и 6.

а)   1 и 3;          б)  1 и 5;          в)  1;          г)  свой ответ.

10. Сколько существует двузначных чисел кратных 11, но не кратных 33?

а)   6;          б)  5;          в)  4;          г) свой ответ.

 

 

Тест

 

Преобразование алгебраических выражений

Вариант №1

1. Расположите в порядке возрастания числа:

1) m,n,p               2) n,m,p               3) m,p,n                         4) p,m,n

 2. Упростите выражение: (3c – 2)² + 24c.

1) (3c + 2)²           2) 3c² + 2              3) 3c² - 4               4) 9c² - 4

 3. Выразите из формулы  переменную n.

1)        2)         3)                  4)

 4. Упростите выражение: .

1)                   2) 10                    3) 5                4) 2

 5. Выполните вычитание дробей: .

1)                2)                3)              4)

 

 

 

 Тест

Преобразование алгебраических выражений

Вариант 1.

1. Представьте в виде дроби:                     

 

А.

Б.

В.

Г.

 

 

2.Выполните  действия:

А.

Б.

В.

Г.

 

3. Вычислите:

 

 

А. 50,5

Б. 55

В.   5,5

Г.1

 

4. Сравните  числа  и

 

  Ответ _________________________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ИТОГОВЫЙ ТЕСТ №1

  I вариант            

Закрытые задания

Прочитайте задание, подумайте, выберите в предложенных ответах один правильный. За каждый правильный ответ — 2 балла.

№	Текст задания	Варианты ответа
1.	Выберите дробные выражения 1) m2 – n2                                         3)  a : (a + 6) 2)                  4)	А   2;3 Б   2;4 В   1; 4 Г   3; 4
2.	Укажите корни квадратного уравнения 2х2 = 3х.	А   0; 1,5 Б   0 В   0; – 1,5 Г   1,5
3.	Вычислите .	А   0,6 Б    0,6 В   6 Г    6
4.	Сократите дробь  .	А   а – 4 Б   В   Г   4 – а
5.	Какое из уравнений не имеет корней?	А   2х2 + 5х + 6 = 0 Б   х2 + 8х + 16 = 0 В   3х2 + х – 7 = 0
6.	Вычислите .	А   0,5 Б   8 В   16 Г
7.	При каких значениях х функция   у = – 5х  принимает  значения больше 7,5?	А   (– ; 1,5) Б   (– ; – 1,5) В   (– ; – 1,5] Г   (12,5; + )
8.	Выберите выражение, которое не имеет смысла при а = 0 1)                            3)  2)                       4)  .	А   1 Б   1; 3 В   1; 4 Г   2
9.	Расположите числа в порядке возрастания ; 2; 3.	А   ; 2; 3 Б   3; 2; В   ; 3; 2 Г   2; 3; Д  2;  ;  3
10.	Сумма квадратов трех последовательных натуральных чисел равна 3024. Найдите эти числа. Решая эту задачу, ученик составил уравнение n2  + (n – 1)2 + (n + 1)2 = 3024. Что он обозначил буквой n?	А   наименьшее число Б   наибольшее число В   среднее число
11.	При каких значениях х имеет смысл выражение ?	А   [; + ) Б   [1,6; + ) В   (– ;  1,6] Г   (– ; ]
12.	Выполните действие .	А        В   х (х – а) Б        Г
13.	Решите уравнение 4х2 – 25 = 0	А     6 Б    – 2,5; 2,5 В     2,5 Г    ; –
14.	Решите систему неравенств .	А   (– 3; 6) Б   [– 3; 6] В   [6; + ) Г   (6; + )
15.	Какое квадратное уравнение имеет корни 4 и 9?	А   х2 + 13х + 36 = 0 Б    х2 + 36х + 13 = 0 В   х2 – 36х + 13 = 0 Г   х2 – 13х + 36 = 0
16.	Внесите множитель под знак корня  – 7.	А   Б   – В   – Г   –
17.	Приведите дробь  к знаменателю а2 – b2.	А   В   Б     Г
18.	Решите неравенство   х – 4 < 3 х + 9.	А   (– 6,5; + ) Б   [– 6,5; + ) В   ( 6,5; + ) Г   (– ; – 6,5)
19.	Выберите неполные квадратные уравнения 1)  х2 – 6х  = 0; 2)  3х2 – 11  = 0; 3) – х2 + 2х  = 3; 4)  – х2 – 11  = 3х.	А   1; 2 Б   1; 3 В   2; 4 Г   3; 4
20.	Из данных чисел выберите то, которое записано в стандартном виде.	А   51,24 ∙106 Б   0,011 ∙ 10-2 В   2,2145 ∙ 104 Г   0,02

ОТКРЫТЫЕ  ЗАДАНИЯ

Выполните задания, решение оформите на отдельном листе. Мысли выражайте  логично, последовательно. Максимальное число баллов за открытые задания — 43 .

№, балл	Текст задания
21. 5 б.	Решите уравнение х2 + 2х  – 63 = 0.
22. 4 б.	Сократите дробь .
23. 6 б.	Упростите выражение  (.
24. 4 б.	Постройте график функции у = .
25. 6 б.	Найдите сумму целых решений системы неравенств .
26. 2 б.	Освободитесь от знака корня  в знаменателе дроби .
27. 2 б.	При каком значении а графики функций у = х2 и у = – 2х + а не пересекаются?
28. 4 б.	Упростите () ∙ .
29. 5 б.	Решите неравенство 0,5х – 3 < 2х – 1.
30. 5 б.	Упростите выражение .

 

Итоговый тест №1                                                                                                              1 вариант

 

За любое верное решение дается максимальный балл.

№, балл	Решения и указания	Балл за этап решения
21.   5 б.	За определение коэффициентов квадратного уравнения а = 1, b = 2, с = – 63. За нахождение дискриминанта D = 256. За нахождение корней уравнения х1 = – 9, х2 = 7. За запись ответа.	1 б.   1 б. 2 б. 1 б.
22.   4 б.	За вынесение общего множителя за скобки . За разложение на множители . За сокращение дроби  За запись ответа 3а+ 3.	1 б.   1 б.   1 б.   1 б.
23. 6 б.	За возведение одночлена в степень . За умножение одночленов и получение ответа .	3 б.   3 б.
24. 4 б.	За нахождение области определения функции. За составление таблицы значений. За построение графика функции (за каждую ветвь   графика по 1 б.)	1 б. 1 б. 2 б.
25. 6 б.	За решение первого неравенства  6 – 2х < 3х – 3;    – 5х < – 9; х > 1,8. За решение второго неравенства ;  12 – х  2х;  3х  12; х  4. За решение  системы  неравенств (1,8; 4]. За выбор целых решений и вычисление суммы  2 + 3+ 4 = 9.	2 б.   2 б.     1 б. 1 б.
26. 2 б.	За любое правильное решение. Решение:	2 б.
27. 2 б.	За любое правильное решение. Графики не пересекаются, если уравнение  х2 = –  2х +а не имеет корней. Уравнение  х2  +  2х – а = 0 не имеет корней, если D < 0. Ответ: а .	2 б.
28. 4 б.	За раскрытие скобок 3• 2 + 2 – . За вынесение множителя из-под знака корня  6 + 2 – . За приведение подобных слагаемых и получение ответа 6.	2 б. 1 б.   1 б.
29. 5 б.	За перенос слагаемых из одной части неравенства в другую 0,5х – 2 х  < – 1+ 3. За приведение подобных слагаемых  – 1,5х < 2. За нахождение х (деление на отрицательное число, смена знака) х > ;      х > ;       х > . За запись ответа х.	1 б.   1 б. 2 б.       1 б.
30. 5 б.	За нахождение общего знаменателя и дополнительных множителей  . За нахождение разности дробей . За нахождение произведения . За запись ответа.	2б.     1 б.     1 б.     1 б.

 

 

 

 

 

 

 

 

 

Список рекомендуемой учебно-методической литературы

·         Учебники: Мордкович А.Г., Николаев Н.П. «Алгебра,8», «Алгебра,9». Часть 1. Учебник .Мнемозина, 2006, 2009

·         Мордкович  А.Г. и др.«Алгебра,7», Мордкович А.Г., Рязановский А.Р. «Алгебра,8», «Алгебра,9». Часть 2. Задачник. Мнемозина, 2006, 2009

·         Дидактические материалы: Александрова Л.А. Алгебра. Самостоятельные работы. Мнемозина,2006

·         Дудницын Ю.П. Алгебра,7, Алгебра,8, Алгебра,9. Контрольные работы. Мнемозина,2006  

·         Контрольные и самостоятельные работы по алгебре: 7 класс: к учебнику А.Г.Мордковича и др. «Алгебра 7 класс» / М.А.Попов. – М.: Издательство «Экзамен», 2009.

·          Контрольные и самостоятельные работы по алгебре: 8 класс: к учебнику А.Г.Мордковича и др. «Алгебра 8 класс» / М.А.Попов. – М.: Издательство «Экзамен», 2009.

·          Контрольные и самостоятельные работы по алгебре: 9 класс: к учебнику А.Г.Мордковича и др. «Алгебра 9 класс» / М.А.Попов. – М.: Издательство «Экзамен», 2009.

·         А.А. Максютин, Ю.Н. Неценко, Т.П. Шаповалова. Тренировочные материалы для подготовки к ГИА по математике-2013. Самара: СИПКРО, 2012

·         А.А. Максютин. Математика-9. Учебное пособие для подготовки к выпускным экзаменам за 9 класс и вступительным экзаменам в лицеи, гимназии, математические классы. Самара, 2007.-422с

·         Методические материалы: Мордкович А.Г. Алгебра, 7 -9. Методическое пособие для учителей. Мнемозина,2006

·          Мордкович А.Г. Алгебра, 7 -9.Тесты. Мнемозина,2006

·         Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по геометрии для 7 класса. – М.: Илекса, Харьков: Гимназия, 1999.

·         Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по геометрии для 8 класса. – М.: Илекса, Харьков: Гимназия, 1999.

·         Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и контрольных работ по геометрии для 9 класса. – М.: Илекса, Харьков: Гимназия, 1999.

·         Сборник задач по геометрии в рисунках и тестах. 7-9./Уче6ное пособие. – М.: Аквариум, 1999.

·         Звавич Л.И. Алгебра и начала анализа. 8-11кл.: Пособие для школ и классов с углубленным изучением математики. – М.: Дрофа, 2002.

·         Звавич Л.И. Геометрия. 8-11кл.: Пособие для школ и классов с углубленным изучением математики. – М.: Дрофа, 2000.

 

 

 

 

ИНТЕРНЕТ   ИСТОЧНИКИ

ü  www.ege.moipkro.ru

ü  www.fipi.ru

ü  www.mioo.ru

ü  www.1september.ru

ü  www.math.ru

ü  www.allmath.ru

ü  www.uztest.ru

ü  http://schools.techno.ru/tech/index.html

ü  http://www.catalog.alledu.ru/predmet/math/more2.html

ü  http://shade.lcm.msu.ru:8080/index.jsp

ü  http://www.exponenta.ru/

ü  http://comp-science.narod.ru/

ü  http://methmath.chat.ru/index.html

ü  http://www.mathnet.spb.ru/

ü  http://vip.km.ru/vschool/demo/education.asp?subj=292

ü  http://som.fio.ru/subject.asp?id=10000191

ü  http:// education.bigli.ru

ü  http://informatika.moipkro.ru/intel/int mat.shtml

ü  http://www.informika.ru/; 

ü   http://www.ed.gov.ru/; 

ü  Тестирование online: 5 - 11 классы:      http://www.kokch.kts.ru/cdo/

ü  Педагогическая мастерская, уроки в Интернет и многое другое:      http://teacher.fio.ru

ü  Новые технологии в образовании:      http://edu.secna.ru/main/

ü  Путеводитель «В мире науки» для школьников:       http://www.uic.ssu.samara.ru/~nauka/

ü  Мегаэнциклопедия Кирилла и Мефодия:       http://mega.km.ru

ü  сайты «Энциклопедий», например:      http://www.rubricon.ru/;     http://www.encyclopedia.ru/

 

 

 

Список рекомендованной литературы:

Литература для учителя

1.        Виленкин Н. и др. Математика 5, Математика 6. Москва, «Мнемозина» 2009

2.        Кузнецова Л.В. и др.  Алгебра, сборник заданий. Москва, «Дрофа» 2010

3.        Макарычев Ю.Н. и др. Алгебра 7, Алгебра 8, Алгебра 9 , Москва, «Просвещение»,2009

4.        Пичурин Л.Ф. «За страницами алгебры», Москва: Просвещение, 1990.

5.        Талицкий и М.Л. др. «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся. Москва: Просвещение, 1999.

6.        Тлейзер. Г.И. «История математики в школе VII –VIII Кл.». Пособие для учителей. М.: Просвещение, 1982

7.        Ященко И.В., Семенов А.В., Захаров П.И.. ГИА 2009, Алгебра. Тематическая рабочая тетрадь. 9 класс (новая форма) – М.: Издателство «Экзамен», МЦННМО, 2009 Кочагин В.В., Алгебра: 9 класс: Тестовые задания к основным учебникам: Рабочая тетрадь – М.: Эксмо, 2007

ЛИТЕРАТУРА  ДЛЯ  УЧАЩИХСЯ: 

1.        Большой  справочник «Математика» для школьников и поступающих в ВУЗы. Д.И. Аверьянов и др.  Москва: Дрофа, 1999.

2.        Кордемский Б.А., Ахадов А.А. Удивительный мир чисел. Книга для учащихся.  Москва: Просвещение, 1986.

3.        Кочагин В.В., Алгебра: 9 класс: Тестовые задания к основным учебникам: Рабочая тетрадь – М.: Эксмо, 2007

4.        Ященко И.В., Семенов А.В., Захаров П.И.. ГИА 2009, Алгебра. Тематическая рабочая тетрадь. 9 класс (новая форма) – М.: Издателство «Экзамен», МЦННМО, 2009

 

---