Формирование функциональной грамотности на уроках математики

Формирование функциональной грамотности на уроках математики

• Математике должно учить еще с той целью, чтобы познания здесь приобретаемые, были достаточными для обыкновенных потребностей жизни». Н.И. Лобачевский

Одним из основных отличительных особенностей реализации Федерального Госстандарта является практическая направленность знаний, накопление и использование жизненного опыта ученика, т.е. не «знания для знаний», а «знания для жизни»: Требования стандарта таковы, что наряду с традиционным понятием «грамотность», появилось понятие «функциональная грамотность».

Что же такое «функциональная грамотность»?

Функциональная грамотность – «способность человека решать стандартные жизненные задачи в различных сферах  жизни и деятельности на основе прикладных знаний».

Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.

Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.

Особое место в представлении о функциональной грамотности занимает математическая  грамотность:

Состояние математической грамотности учеников оценивается развитием “математической компетентности”. Математическая компетентность определяется как “сочетание математических знаний, умений, опыта и способностей человека”, которые обеспечивают решение разных проблем, нуждающихся в применении математики.

         Задач, способствующих формированию ключевых компетентностей, в учебниках и дидактических пособиях немного. Поэтому для реализации компетентностного подхода через задачи единственным выходом для школьных учителей является составление компетентностно-ориентированных задач самим.

Рассмотрим несколько примеров использования задач из учебников математики для 5-7 классов, с помощью которых можно составить задание для формирования ключевых компетентностей учащихся.

Задача.

Антон,  Илья и Никита собрали  152 марки. Антон собрал в 3 раза больше марок, чем Никита, а Илья  в 4 раза больше, чем Никита. Сколько марок собрал каждый мальчик?

Эта задача не является компетентностно-ориентированной задачей. Добавив к условию задачи вопрос «постройте круговую диаграмму, изображающую распределение марок (в процентах)», задание становится компетентностно-ориентированной задачей.

Задача   В романе Жюля Верна «Дети капитана Гранта» читаем: «Погода стояла прекрасная, не слишком жаркая…Роберт узнал, что средняя годовая температура в провинции Виктория +74^о по Фаренгейту». Сколько это будет в привычных для нас градусах Цельсия? Составьте формулу для вычисления температуры в градусах Цельсия, если известна температура по Фаренгейту и наоборот.

В таблице  приведена температура таяния льда и кипения воды в градусах Цельсия и по Фаренгейту»

Эта задача является заданием первого уровня, так как учащимся необходимо с помощью таблицы составить формулу и используя эту формулу ответить на вопрос задачи. Для того чтобы задача стала заданием второго уровня, добавим в условие задачи несколько вопросов.

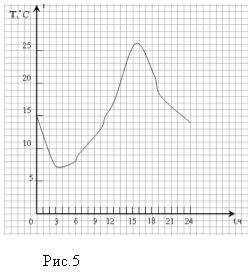
Например: Температура воздуха изменялась в течение дня от  до  Цельсия. На рисунке 5 изображен график изменения температуры. Изобразите график функции, на котором будет изображена температура воздуха в градусах по Фаренгейту, соответствующая температуре на графике.

Эта задача будет заданием второго уровня, так как в ходе решения задачи учащимся необходимо определить значения величин по графику и результатом решения задачи так же будет график.

Задача.  «Редактор  школьной стенгазеты поместил заметку: «На школьных соревнованиях быстрее всех пробежал стометровку ученик 7 «В» класса Аскар. Другие призеры пришли к финишу в таком порядке: Аслан, Паша, Дима. И удивительно – с одной и той же разницей в скорости: Аскар затратил на эту дистанцию 12 с, Аслан – 13 с, Паша – 14 с, Дима – 15 с».

Проверьте, прав ли наш «журналист». Для этого заполните таблицу :

В последней строке поместите разность скоростей каждого мальчика и предыдущего. Действительно ли разница в скорости одна и та же?».

Эта задача является заданием второго уровня, так как решение задачи будет состоять из нескольких шагов, учащимся нужно сравнить получившиеся результаты. Для того, чтобы задача стала заданием третьего уровня можно к условию добавить вопрос: скорость какого из мальчиков ближе к средней скорости бегунов? Результат представьте в виде диаграммы.

Таким образом, задачи из учебника можно использовать в качестве основы для компетентностно - ориентированных заданий.

Дидактические игры на уроках математики по формированию читательской грамотности учащихся:

5-6классы

1.      В начале урока можно предложить игру «Банк идей (гипотез)», куда ученики «складывают» свои мысли о том, что будет сегодня на уроке изучаться. Этот прием научит учеников выдвигать гипотезы исследования и определять, доказаны они или опровергнуты, что очень важно для формирования навыков научно-исследовательской деятельности учащихся при работе с литературой.

2.       «Верные или неверные утверждения», или «Верите ли Вы?» может быть началом урока, когда учащиеся, выбирая «верные утверждения» из предложенных учителем, описывают заданную тему. После знакомства с основной информацией (текст параграфа, лекция по данной теме)мы возвращаемся к данным утверждениям и просим детей оценить их достоверность, используя полученную на уроке информацию.

7-8 классы.Методика «Кластер»

 Кластер (англ. Cluster— пучок, гроздь) — объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определенными  свойствами.  В методике, кластер — это карта понятий, которая позволяет ученикам свободно размышлять над какой-либо темой, дает возможность оценить свои знания и представления об изучаемом объекте, помогает развивать память.

Этапы работы при составлении кластера

1-й этап — посередине чистого листа (классной доски) пишется ключевое слово или словосочетание, которое является «сердцем» идеи, темы.

2-й этап — учащиеся записывают все то, что вспомнилось им по поводу данной темы. В результате вокруг «разбрасываются» слова или словосочетания, выражающие идеи, факты, образы, подходящие для данной темы. Записывается все, что называют учащиеся, ничего не отсеивается.

3-й этап — осуществляется систематизация. После чтения учебника, объяснения учителя, учащиеся начинают анализировать и систематизировать изученный материал. Хаотичные записи слов-ассоциаций объединяются в группы, в зависимости от того, какую сторону содержания отражает то или иное записанное понятие, факт. Ненужное, ошибочное зачеркивается.

4-й этап — по мере записи появившиеся слова соединяются прямыми линиями с ключевым понятием. У каждого из «спутников» в свою очередь тоже появляются «спутники», устанавливаются новые логические связи. В итоге получается структура, которая графически отображает наши размышления, определяет информационное поле данной темы.

Методический прием — «Инсерт». Технически он достаточно прост. Учащихся надо познакомить с рядом маркировочных знаков и предложить им по мере чтения ставить их карандашом на полях специально подобранного и распечатанного текста. Помечать следует отдельные абзацы или предложения в тексте. Пометки могут быть следующие:

В 9-х классах для формирования всех видов функциональной грамотности, как нельзя лучше,  подойдут задания 1-5 из варианта ОГЭ

Практико-ориентированные задания нового типа для 9 класса (ОГЭ)

Задача о садовом участке

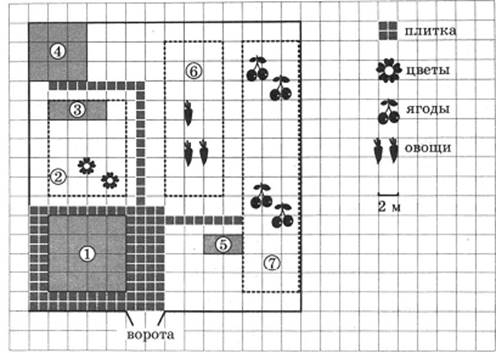
На плане изображен дачный участок по адресу: СНТ Рассвет, ул. Морская, 7 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота.

Площадь, занятая жилым домом, равна 64 кв. м. Помимо жилого дома, на участке есть баня, к которой ведет дорожка, выложенная специальным садовым покрытием. Между жилым домом и баней находится цветник с теплицей. Теплица отмечена на плане цифрой 3.

Напротив жилого дома находится бак с водой для полива растений, за ним плодово-ягодные кустарники. В глубине участка есть огород для выращивания овощей, отмеченный цифрой 6.

Все дорожки внутри участка имеют ширину 1 м и застелены садовым покрытием, состоящим из плит размером 1м х 1м. Площадка вокруг дома выложена плитами такого же размера, но другой фактуры и цвета.

 К дачному участку проведено электричество. Имеется магистральное газоснабжение.

1.                           Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.

Ответ :1254

2. Плиты для садовых дорожек продаются в упаковке по 6 штук. Сколько упаковок плит понадобилось, чтобы выложить все дорожки и площадку вокруг дома?

Решение:   дорожка от дома до бани имеет 22 плитки, дорожка от дома кустарников – 8 плиток,  площадка вокруг дома –

14 ∙ 11 – 8∙ 8 = 154-64 = 90 . Итого: 30 + 90 =120 плиток

120:6 = 20 упаковок

Ответ :20

3.      Найдите площадь бани. Ответ дайте в квадратных метрах. 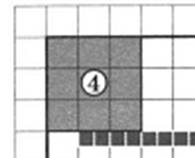Решение: S = a² = a ∙ а – площадь квадрата

1 кл=2м, значит а= 6м

S _бани= 6 х 6 =36 м²

Ответ : 36

4.Найдите суммарную площадь плитки на прямоугольной площадке вокруг дома. Ответ дайте в квадратных метрах.

Решение: S = a ∙ b – площадь прямоугольника

1 кл=2м ;1 кл=2плиткам по 1м, значит а= 14м, b = 11м,

дом –квадрат, сторона = 4∙2м=8м

                                       S _{площадки} = 14 х 11 - 8 х 8 = 90 м²

Ответ : 90

5. Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое и газовое отопление. Цены на оборудование  и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

Решение: стоимость оборудования и монтажа:

22000 +16412= 38412 руб. - газ ; 18000 + 12000 = 30000 руб. электр. отоп.

Разница между стоимостью установки: 38412 – 30000 = 8412 руб.

Расход 1 часа обогрева : 1,3 куб. м/ч ∙ 4,4 руб./ куб. м =5,72 руб./ч –газ

4,7 руб./ куб. м ∙ 4,2 руб./(кВт ∙ ч) = 19,74 руб./ч  - электричество

Разница между стоимостью потребления за 1 час: 19,74 - 5,72 = 14,02 руб./ч

Через сколько часов экономия от использования газа компенсирует затраты:

8412 руб. : 14,02 руб./ч  = 600ч

Ответ : 600

Для решения проблемы, связанной с жизненной ситуацией, математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленную в контексте реального мира, и сформулировать ее на языке математики.  Это преобразование требует математических рассуждений и, возможно, является центральным компонентом того, что значит быть математически грамотным в современном мире.