МБОУ «Лицей №177» Ново-Савиновского района г. Казани

III Республиканская научно-практическая конференция имени Александра Михайловича Бутлерова Секция: «Математика»

Научно – исследовательская   работа

«Формула пика»

Номинация «  математика »

Выполнила:  Зарипов Ильяс Фаязович,

                                                                       ученик 9 класса

                                                                        МБОУ Большенырсинская СОШ

                                                                      Тюлячинского МР РТ

                                                        Руководитель  :  

                                                          Зарипова Лилия Габдрауфовна

                       учитель математики первой

                                                       квалификационной категории,

                                                       МБОУ Большенырсинская СОШ

                                                       Тюлячинского муниципального района РТ

2022 год

Содержание

ВВЕДЕНИЕ. 3

ИСТОРИЧЕСКАЯ СПРАВКА.. 4

1.   СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ.. 6

3.    ФОРМУЛА ПИКА.. 9

4.   УЗЛЫ НА ОТРЕЗКЕ. 14

5.   ПРИМЕНЕНИЕ ФОРМУЛЫ ПИКА ПРИ ВЫПОЛНЕНИИ ЗАДАНИЙ ЕГЭ ПО МАТЕМАТИКЕ. 17

ЗАКЛЮЧЕНИЕ. 21

СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ РЕСУРСОВ.. 22

ВВЕДЕНИЕ

Актуальность:

Формулу Пика можно применять при вычислении площади фигуры, изображенной на клетчатой бумаге (это здание В₃ в контрольно-измерительных материалах ЕГЭ по математике).

Объект исследования: задачи на клетчатой бумаге

  Предмет исследования: задач на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

  Методы исследования: моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.

• Цель исследования:

1.      Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника.

2.      Области применения искомой формулы.

     Для достижения поставленной цели предусматриваем решение следующих задач:

• Подобрать необходимую литературу
• Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
• Проанализировать и систематизировать полученную информацию
• Найти различные методы и приёмы решения задач на клетчатой бумаге
• Создать электронную презентацию работы для представления собранного материала одноклассникам.

• Гипотеза: Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формулам площадей из учебника математики.

Многообразие задач на бумаге в клеточку, их «занимательность», отсутствие общих правил и методов решения  вызывают у школьников затруднения при их рассмотрении

       При решении задач на клетчатой бумаге нам понадобится геометрическое воображение и достаточно простые геометрические сведения, которые известны всем.

ИСТОРИЧЕСКАЯ СПРАВКА

       Георг Александр Пик – австрийский математик, родился 10 августа 1859 года в Вене. Мать его – Йозефа Шляйзингер (JosefaSchleisinger), отец – Адольф Йозеф Пик (AdolfJosefPick) – будучи руководителем частного института, предпочёл до одиннадцати лет обучать сына на дому, а затем отдал его в четвёртый класс гимназии. В 1875 году Г.А. Пик сдал выпускные экзамены и поступил в Венский университет.

       В 1876 году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику, университет окончил в 1879 году, получив возможность преподавать оба эти предмета. 16 апреля 1880 года Пик защитил докторскую диссертацию «О классе абелевых интегралов» .

       После защиты диссертации его утверждают на должность ассистента одного из ведущих физиков того времени, профессора Эрнста Маха, являющегося одновременно ректором Карлова университета в Праге – старейшего учебного заведения во всех славянских странах. За исключением академического 1884-1885 года, который Пик провёл в Лейпцигском университете, учась у Феликса Кляйна, он оставался в Праге до конца своей карьеры. В 1888 году он был назначен экстраординарным профессором математики, а затем ординарным профессором ( полным профессором) в 1892 году в немецком университете в Праге.

В 1882 году произошло разделение Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 году, он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры.

 В 1900-1901 годах Георг Пик был деканом философского факультета Карлова университета и в 1911 году Пик оказался во главе комиссии, которая приняла на кафедру математической физика Альберта Эйнштейна. Они становятся близкими друзьями, совершая длительные пешие прогулки и беседуя, вместе музицируют.

Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольникас вершинами в узлах клетки. В Германии эта теорема включена в школьные учебники. Широко известна она стала только лишь в 1969 году, после того, как Гуго Штейнгауз включил её в свою знаменитую книгу «Математический калейдоскоп».

       После того как Пик вышел в отставку в 1927 году, он получил звание почётного профессора и вернулся в Вену — город, в котором он родился. Однако в 1938 году после аншлюса (присоединение) Австрии 12 марта он вернулся в Прагу. За десять лет до того, в 1928 году, Пик был избран членом-корреспондентом Чешской академии наук и искусств, но в 1939-м, когда нацисты заняли Прагу, он был исключён из академии.
13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

1.                     СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ

Существует несколько способов вычисления площади  многоугольника на клетчатой бумаге:

·                   Подсчет  количества клеток

·                   Применение формул планиметрии

·                   Разбиение  фигуры на более простые фигуры

·                   Достроить фигуру до прямоугольника

·                   Формула Пика

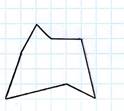Найдём площадь многоугольника (рис. 1).

Искать её можно по-разному.

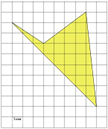
Это задание нам дал наш учитель на уроке. Хотя многоугольник выглядел достаточно просто, для вычисления его площади нам пришлось изрядно потрудиться. Мы потратили 15 минут времени на решение этой задачи. Хочу отметить, что не все учащиеся нашего класса справились с данным заданием. А когда нам сказали, что есть формула позволяющая вычислить площадь за одну минуту, то меня очень заинтересовало и я решила заняться изучением этого вопроса.

Сначала я решила узнать какими способами вычисляли площадь мои одноклассники, кто справился с заданием и заняться изучением формулы. В нашем классе не кто не знал формулы Пика. Также это задание мы решили дать учащимся 9 и 11 классов. Вот что у нас получилось.

1способ:Подсчет  количества клеток (для данной фигуры приближенный).

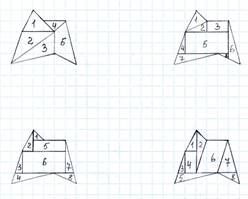
2 способ: попробовать разрезать многоугольник на достаточно простые фигуры(рис.2), найти их площади и сложить. Однако, это очень хлопотно!

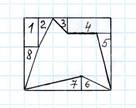3 способ: вычислить площадь фигуры (рис.3), которая дополняет многоугольник до прямоугольника, и вычесть эту площадь из площадипрямоугольника. Дополненная фигура (в отличие от исходного многоугольника) легко разбивается на прямоугольники и прямоугольные треугольники так, что её площадь вычисляется без усилий.

S = 2+1+0,5 + 3+ 2 + 1 + 2 +1,5=13 (кв.ед.)

Следовательно,  площадь исходного многоугольника равна

S = 5・6 – 13=17 (кв.ед.)

3 способ: Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислить гораздо проще: существует формула, связывающая площадь такого многоугольника с количеством узлов, лежащих внутри и на границе многоугольника.

По формуле Пика S=В+Г:2–1, гдеВ количество узлов, лежащих внутри прямоугольника, а Г – количество узлов на его границе.

S = 14 + 8/2 – 1 = 17(кв.ед.)

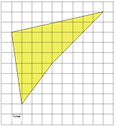
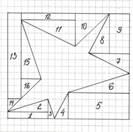Задача: Вычислить площадь звезды (рис 4)

Решение:1 способ:

Используя формулы для вычисления площади прямоугольника и площади треугольника, вычислю площади фигур 1-16.

 кв.ед.;   кв.ед.;  кв.ед. ; кв.ед. ;  кв.ед.;

S₆= 13,5 кв.ед.;S₇ = 9  кв.ед.; S₈ = 9  кв.ед.; S₉ = 18  кв.ед.; S₁₀ = 12,5 кв.ед.; S₁₁ = 16 кв.ед.; S₁₂ = 8 кв.ед.; S₁₃ = 26  кв.ед.; S₁₄ = 2  кв.ед.; S₁₅ = 13,5 кв.ед.;  S₁₆ = 4,5 кв.ед.

Площадь большого прямоугольника равнаS¹=16∙18=288 кв. ед.

Найду сумму площадейS₁ + S₂ +…+S₁₆ =185,5 кв.ед.

Следовательно, площадь многоугольника равна S=288-185,5=102,5 кв.ед.

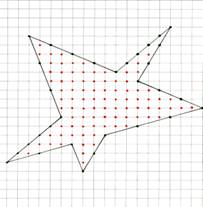2 способ: с помощью формулы Пика

1.                     Сосчитаю количество внутренних узлов. В=88(красные точки рис. 5).

2.                     Сосчитаю граничные узлы. Г=31

(чёрные точки рис. 5).

3.                     Применю формулу Пика.

S=88+31:2-1 = 88+15,5-1=102,5(кв.ед)

Ответ: 102,5 кв.ед.

3. ФОРМУЛА ПИКА

Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат).

      Линии, идущие по сторонам клеток, образуют на нём сетку, а вершины клеток – узлы этой сетки.

Пусть дан некоторый решётчатый многоугольник, с нулевой площадью. Обозначим его площадь черезS: количество точек с целочисленными координатами, лежащих строго внутри многоугольника – через В; количество точек с целочисленными координатами, лежащих на сторонах многоугольника – через Г.

Тогда справедлива формула  S=В+Г:2 – 1, которую открыл и доказал австрийский математик Георг Александр Пик в 1899 году. Докажем её.

Доказательство проведу в несколько этапов: от самых простых фигур до произвольных многоугольников:

1.                     Единичный квадрат. В самом деле, для него S=1, В=0, Г=4, и формула верна.

2.                     Прямоугольник со сторонами, параллельными осям координат. Для доказательства формулы обозначу через а и bдлины сторон прямоугольника. Тогда нахожу: S = a·b, В = (а-1)(b-1), Г=2(а+b). Непосредственной подстановкой убеждаюсь, что формула Пика верна.

3.                     Любой треугольник, расположенный на клетчатой бумаге, внутри которого нет узлов, а на его границе узлами являются только вершины треугольника, имеет площадь 0,5 кв.ед. Такие треугольники называются примитивными. Следовательно, справедливо следующее утверждение:

Все примитивные треугольники равновелики и их площади равны половине  площади единичного квадрата.

Множество примитивных треугольников разнообразно (рис.6).

Связь между площадью фигуры и количеством узлов, попавших в эту фигуру, особенно ясно видна в                           случае прямоугольника.

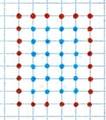
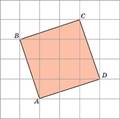
   Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рис. 7).

    Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов      на его границе. Сместим сетку на полклетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна S = В +  + 4 ·  = В +  - 1 .

    Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу.

Это равенство можно доказать другим способом. Если стороны прямоугольника равны а и в (рис.), то его площадь равна S=ав, число внутренних узлов равно В=(а-1)(в-1), а граничных – Г=2(а+в).

В+Г:2-1=(а-1)(в-1)+(а+в)-1=ав-а-в+1+а+в-1=ав=S

Пусть многоугольник М разрезан на многоугольники

М₁  и М₂ с вершинами в узлах. Докажем, что S_M = S_M1 + S_M2

Доказательство: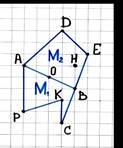Рассмотрим рис.8.Пусть многоугольник АДЕВСКР (многоугольник М) разрезан отрезком АВ на два многоугольника:

АВСКР (M₁) иАВЕД (M₂).

Сосчитаю внутренние и граничные узлы каждого многоугольника. Если узел внутренний для М и не лежит на отрезке АВ (как, например, точка Н), то он внутренний или для или для, поэтому его «вклад» в выражение S_M и в сумму S_M1 + S_M2  одинаков.

Одинаковым будет и «вклад»  каждого узла, не лежащего на отрезке АВ (например, Д): он равен 0,5.

Осталось рассмотреть узлы, лежащие на отрезке АВ. Если такой узел лежит между А и В (как, например, точка О), то для многоугольника М он внутренний, а для многоугольников M₁ и M₂ - граничный. Поэтому его «вклад» в S_M равен 1, а в каждое из выражений S_M1 + S_M2 – по 0,5. Замечу, что «вклады» такого узла в S_M и S_M1 + S_M2 равны.

Наконец, рассмотрю узлы A и B. Они граничные как для M, так и для M₁, M₂. Поэтому «вклад» каждого их этих узлов в S_M равен 1, а в S_M1+S_M2 равно 1, что на 1 меньше, чем их «вклад» в S_M1+S_M2. Но S_M=B_М+Г_М2-1, а S_М1+S_М2=В_М1 + Г_М1 –1 + ВМ₂ + Г_М2– 1 =В_М1+В_М2+Г_М1+Г_М2 – 2, так что из общего «вклада» всех узлов вычитается 1, а в (S_М1+S_М2) вычитается 2, и это компенсирует разницу «вкладов» узлов A и B.

Итак,  S_M= S_М1+S_М2.

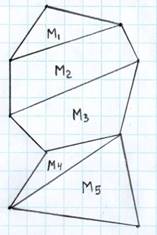Представлю, что многоугольник М с вершинами в узлах сетки можно разрезать на k многоугольников каждый из которых также имеет вершины в узлах сетки (рис.10).

Если я буду выполнять это разрезание шаг за шагом: сначала отрежу , потом , и так далее, до , то на каждом шаге я смогу воспользоваться формулой Пика. В результате получу равенство.

Докажу формулу Пика для произвольного треугольника с вершинами в узлах сетки.

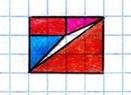 Любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямоугольников и прямоугольных треугольников с катетами на линиях         сетки (рис.11).

А так как формула Пика верна для таких прямоугольников и прямоугольных треугольников, то она верна и для исходного треугольника.

Если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

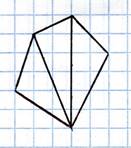У меня возник вопрос: а всякий ли многоугольник с вершинами в узлах можно разрезать на такие треугольники?

Если все углы многоугольника меньше 180°, т.е. многоугольник выпуклый, то его можно разрезать на треугольники, например, проведя диагонали, соединяющие одну из его вершин со всеми остальными (рис.12)

   Рис. 12

Следовательно, формула Пика верна для всех выпуклых многоугольников.

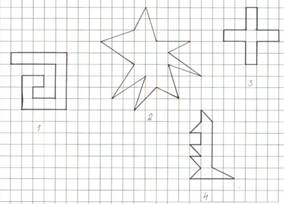Опять вопрос: а выполняется ли формула Пика для невыпуклых многоугольников? Я решила на конкретных примерах проверить формулу Пика для таких многоугольников (рис.13).

Решение:

1)         S=0+32:2-1=15 кв.ед

2)         S=18+17:2-1=25,5 кв.ед

3)         S=0+20:2-1=9 кв.ед

4)         S =0+19:2-1=8,5кв.ед

8. Вычислить площадь фигуры РИС. 14

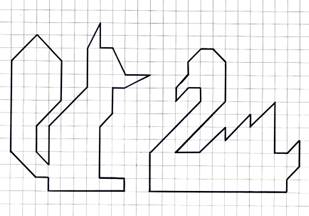Решение:

1) В = 44, Г = 57, S=44+57:2-1=71,5 кв.ед.

2) В = 40, Г = 54, S=40+54:2-1=66 кв.ед.

Ответ.71,5 кв.ед.; 66 кв.ед.

4.                     УЗЛЫ НА ОТРЕЗКЕ

Неудобство формулы Пика состоит в том, что уж очень четким должен быть чертеж и очень внимательно нужно его рассматривать, чтобы определить, лежит ли данный узел внутри фигуры или же попал на ее границу. Как точно сосчитать число узлов на границе? Поскольку граница состоит из отрезков, то меня заинтересовал вопрос о количестве узлов сетки, лежащих на произвольном отрезке с концами в узлах.

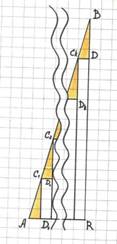Пусть А и В – узлы сетки. Обозначу через первый узел, встретившийся после А на отрезке АВ (значит, между точками А и  больше узлов нет). Построю прямоугольный треугольник АC₁D₁ с гипотенузойAC₁ и катетами, лежащими на линиях сетки (рис.14).

ЕслиC₁≠В, то смещу этот треугольник вдоль отрезка АВ на расстояние АC₁. Получу равный ему треугольник C₁C₂D₂.Следовательно,C₂ узел, и между C₁ и C₂нет узлов. Ясно, что если эту процедуру продолжить, то когда–нибудь в качестве очередной точки  C_k+1 можно получить точку В – узел сетки. Рассматривая большой прямоугольный треугольник АRВ с гипотенузой АВ, прихожу к выводу:

AR = (k +1)AD₁, BR = (k +1)C₁D₁, AB = (k +1)AC₁.

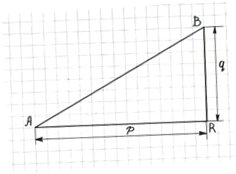
Сколько же узлов лежит между точками А и В (считаем, что А и В не лежат на одной линии сетки). Построю прямоугольный треугольник АRВ с вершинами в узлах сетки и с гипотенузой АВ (рис.15).Пуcть АR =р, BR=q. Очевидно, что p и q – целые положительные числа.

Теорема. Если p и q- взаимно просты, то между А и В на отрезке АВ нет узлов сетки. Если же наибольший общий делитель p и q равен n, где n>1(НОД (p, q)=n>1), то на отрезке АВ между точками А и В расположено ровно (n-1) узлов сетки.

Доказательство:

1)                    Пусть числа p и q взаимно просты. Если между А и В были k узлов

(k 1),  то, взяв ближайший узел к А узел , получу по формулам:

p=(, q, т.е. p и q имеют общий делитель (, больший 1. Но ведь они взаимно просты.

2)  Пусть НОД(p, q)= n>1. Поделю отрезок АR и ВR на n равных частей, опять прихожу к рис.10,- какие-то узлы сетки и k=n-1. Таким образом в этом случае между точками А и В есть хотя бы n-1 узел. Следовательно, если самый большой общий делитель чисел p и q  равенn, то между А и В ровно n-1 узел. Зная, это, можно не мучаясь сомнениями с уверенностью сказать, через сколько узлов проходит произвольный отрезок с концами в узлах сетки.

Сколько клеток рассекает на две части диагональ прямоугольника mn, где m и n взаимно простые числа?

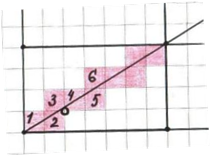Замечу, что диагональ такого прямоугольника не проходит через узлы. Буду считать, что диагональ идет из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку №1), потом она попадает в клетку №2 (рис.16),  и так далее.

                      Рис. 16

Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечет после клетки с номером k.

Итак, я получила «цепочку», идущую из левого нижнего угла в правый верхний. Мне необходимо понять, чему равно число клеток в этой цепочке. Дам каждой клетке адрес (t;s), если она расположена в горизонтальном ряду с номером t , и вертикальном ряду с номером s. Левый нижний угол получает адрес (1;1) а правый верхний – (m;n). Замечаю, что при переходе от клетки с номером k в нашей цепочке к клетке с номером k+1 сумма чисел t и s в адресе возрастает точно на 1. Значит, чтобы перейти от клетки с адресом (1;1) к клетке с адресом  (m;n), надо сделать ровно m+n-2 шагов, пройдя, таким образом, m+n-1 клеток.

Пусть m и n – произвольные натуральные числа. Сколько клеток рассекает диагональ прямоугольника mxn?

Пусть d – НОД (m;n). Очевидно, что вдоль диагонали исходного прямоугольника образуется d маленьких прямоугольников  Стороны этих маленьких прямоугольников  уже взаимно просты, поэтому их диагонали рассекают по  -1 клеток каждая. Значит, диагональ исходного прямоугольника рассечет  ( -1)d=m+n-d клеток.

В прямоугольнике mxn диагональ рассекает m + n - НОД(m;n) клеток.

Например, если m и n взаимно просты – то m+n-1 клеток.

 ПРИМЕНЕНИЕ ФОРМУЛЫ ПИКА ПРИ ВЫПОЛНЕНИИ ЗАДАНИЙ ЕГЭ ПО МАТЕМАТИКЕ

Все пособия по подготовке к ЕГЭ, диагностические работы, которые проводит Центр тестирования, а также демонстрационный вариант, содержат задания на вычисление площадей фигур, изображенных на клетчатой бумаге. Это задание В₃.Большинство таких заданий можно быстро выполнить, применив лишь формулы для вычисления площадей треугольника, прямоугольника, квадрата и трапеции. 

Примеры:

На клетчатой бумаге с клетками размером 1 см× 1 см  изображен  треугольник (трапеция) (см. рисунок). Найдите его площадь в квадратных сантиметрах:

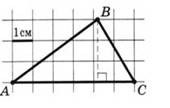
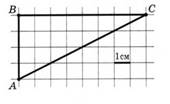
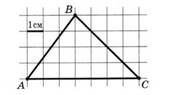
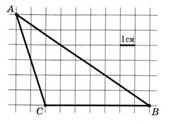
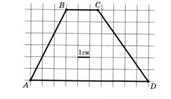
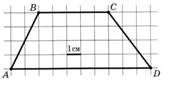
Но в некоторых вариантах применение формул площадей фигур приводит к более объемному решению, чем использование формулы Пика. S = В + Г : 2 – 1, где В – количество улов внутри фигуры, Г – количество узлов на границе фигуры.

Примеры:

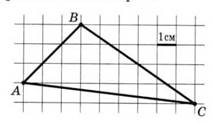1.  На клетчатой бумаге с клетками размером 1см × 1см  изображен треугольник. Найдите его площадь в квадратных сантиметрах.

I способ.

Из площади прямоугольника вычтем сумму площадей трех треугольников:

II способ.Применяем формулу Пика: S = В + Г : 2 – 1, где В – количество узлов внутри фигуры, Г – количество узлов на сторонах фигуры.

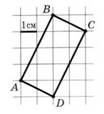  В=13, Г=6, S = 13 + 6 : 2 – 1 = 15(см²)

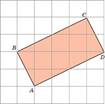
2.  На клетчатой бумаге с клетками размером 1см × 1см  изображен прямоугольник. Найдите его площадь в квадратных сантиметрах.

  В=8, Г=6, S = 8 + 6 : 2 – 1 = 10(см²)

3. Найдите площадь фигур, изображенного на клетчатой бумаге с размером клетки 1см × 1см. Ответ дайте       в квадратных сантиметрах.

1)        В = 9, Г = 8,

      S = 9 + 8 : 2 – 1 = 12(см²)

2)     В = 8, Г = 5,

      S = 9 + 5 : 2 – 1 = 10,5(см²)

3)        В = 6, Г = 5,

      S = 6 + 5 : 2 – 1 = 7,5(см²)

4)      В = 10, Г = 7, 

      S = 10 + 7 : 2 – 1 = 12,5(см²)

5)      В = 9, Г = 4,

      S = 9 + 4 : 2 – 1 = 10(см²)

6)       В = 5, Г = 4,

      S = 5 + 4 : 2 – 1 = 6(см²)

7)  В = 9, Г = 12,

      S = 9 + 12 : 2 – 1 = 14(см²)

8)   В = 8, Г = 6,

      S = 8 + 6 : 2 – 1 = 10(см²)

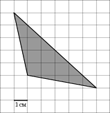
9)     В = 9, Г = 8,

     S = 9 + 8 : 2 – 1 = 12(см²)

10)  В = 22, Г = 12, S = 22 + 12 : 2 – 1 = 26(см²)

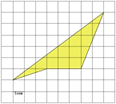
11)   В = 10, Г = 7, S = 10 + 7 : 2 – 1 = 12,5(см²)

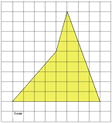
14)     В = 25, Г = 13,  S = 25 + 13 : 2 – 1 = 30,5(см²)

ЗАКЛЮЧЕНИЕ

Умение пользоваться формулой Пика позволяет вычислять площади выпуклых многоугольников, а так же площади невыпуклых многоугольников. А значит, ее можно применять для вычисления площадей многоугольников в задании В₃ на ЕГЭ.

ü     Для вычисления площади  многоугольника, нужно знать всего одну формулу: S = В + Г/2  - 1- формулу Пика.

ü     Формула Пика проста для запоминания.

ü     Формула Пика удобна и проста в применении.

ü     Многоугольник, площадь которого необходимо вычислить, может быть любой формы.

Формула Пика облегчает и ускоряет нахождение площади многоугольников. Но и она имеет свои недостатки:

1. Чертёж должен быть очень четким (для подсчета узлов);

2. Формула применяется лишь в том случае, если многоугольник изображен на клетчатой бумаге;

3. Формула не имеет аналогов в пространстве.

       Некоторые задачи в работе решены несколькими способами. Я познакомил своих одноклассников с формулой Пика и провел небольшую самостоятельную работу. Ребятам предлагалось вычислить площадь многоугольника, применяя названную формулу. По итогам этой работы можно сделать вывод, что на вычисление площади невыпуклого многоугольника с помощью формулы Пика было затрачено меньше времени, и не было допущено ошибок. Моей работой заинтересовались учащиеся 11 класса, после знакомства  с формулой Пика они спросили почему их с этой формулой не познакомили раньше.

      Эта работа способствовала более глубокому пониманию школьной программы и расширению кругозора.

СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ РЕСУРСОВ

1.                 Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.

2.            Задачи открытого банка заданий по математике ФИПИ

3.            Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.

Интернет ресурсы

• http://interneturok.ru

• http://live.mephist.ru

• http://mathege.ru

• ilib.mccme.ru

• le-savchen.ucoz.ru

• reshuege.ru

• diductio.ru

Скачано с www.znanio.ru