Формулы приведения

Тема: Формулы приведения.

 Тип урока: изучение нового материала.

Цели урока:

Образовательные- введение формул приведения; формирование умений и навыков применения формул приведения при преобразовании тригонометрических выражений и решении простейших тригонометрических уравнений; добиться усвоение темы всеми учащимися.

Развивающие: Формирование представления о математике как о необходимой для каждого человека составляющей общих знаний о мире и понимание значимости математических знаний для активного использования человеком в быту, в профессиональной деятельности, развитие логического мышления, внимания.

Воспитательные: развитие познавательного интереса, развитие познавательности, развитие умений преодолевать трудности при решении математических задач.

Оборудование: учебник А.Г.Мордкович А-10 , справочные материалы, доска, раздаточный материал.

План урока.

I. Организационный момент

II. Постановка целей и задач урока.

III. Изучение нового материала.

IV. Закрепление изученного материала.

V.  Подведение итогов.

VI. Домашнее задание.

Ход урока.

I.Организационный момент:

·         приветствие

·         проверка присутствующих учеников на уроке.

II. Постановка целей и задач урока:

Учитель делает краткий обзор темы и целей урока.

     Деятельность учащихся: постановка целей урока;  беседа; работа с учебником;                                   обобщение.

фронтальная устная работа: контрольные вопросы;    

1. Почему окружность называется единичной?
2. Назвать координаты точек пересечения окружности с осями координат.
3. Какие знаки имеют абсциссы и ординаты всех точек, лежащих в первой четверти, второй, третьей, четвертой?
4. Какое местоположение точки считается начальным?
5. Какой угол считаем положительным, а какой отрицательным?

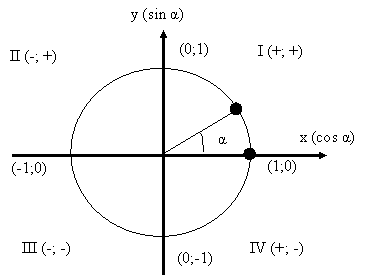
6.Определите четверть в которой располагается данный угол: а) 194⁰, 120⁰, 372⁰, 278⁰.

III. Изучение нового материала:

1. Вводное слово учителя

. - Здравствуйте, ребята! Мы продолжаем с вами изучать тригонометрические формулы, занимающие важное место в курсе математики.

- Они позволяют привести значение тригонометрических функций к более удобным для данной задачи углам).  Выражения типа ,   и т.п. можно упростить настолько, что они будут состоять лишь из одного аргумента α.         

- А раз они ПРИВОДЯТ,  как бы вы их назвали?

- Сформулируйте тему нашего урока:  Формулы приведения.

- Итак, сегодня на уроке мы познакомимся с формулами приведения, научимся применять их при преобразовании тригонометрических выражений.

- Формул приведения очень много. Запомнить их трудно – но самое главное, в этом нет необходимости. Достаточно запомнить одно-единственное правило – и вы легко сможете самостоятельно выводить формулы и упрощать выражения.

Формулировка правила:

Первое правило:  Если в левой части формулы угол равен , то синус заменяется на косинус, косинус – на синус, тангенс – на котангенс и котангенс – на тангенс (функция меняется на кофункцию).  Если угол равен , то замены не происходит.

Второе  правило:  В правой части формулы ставится тот знак, который имеет левая часть при условии 0<α<π/2.

Примеры на первое правило:

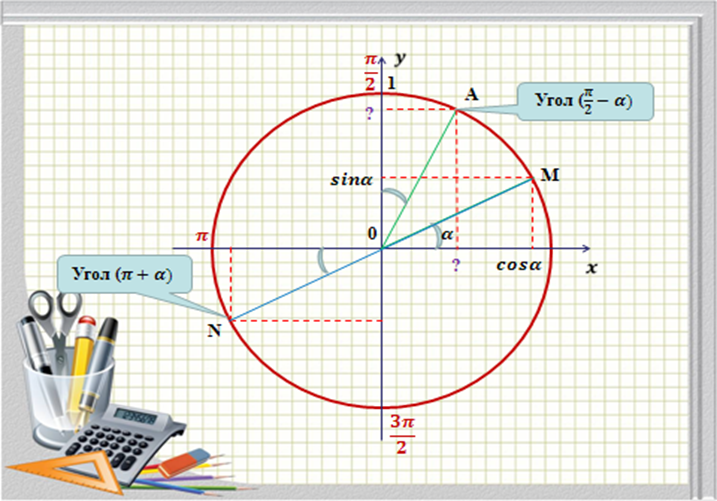
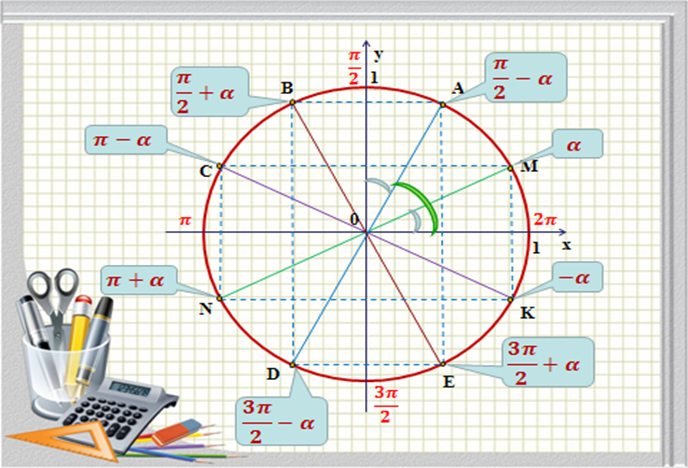
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется.

1) 

2) 

3) 

4) 

Для аргументов вида наименование функции следует изменить на кофункцию.

5) 

6) 

7) 

8) 

Для аргументов вида наименование функции не меняется.

Индивидуальная работа по заполнению таблицы

Учащимся предлагается заполнить таблицы.

Формулы приведения

Где же применяются формулы приведения?

Одно из применений – это нахождение значений тригонометрических функций различных углов.

 - упрощение тригонометрических выражений.

  И напоследок притча:

«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. Кто откроет тот и будет первым помощником. Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.

Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы и не боишься сделать попытку.»

IV ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА.

V.  Подведение итогов.

 - Ребята, наш урок подходит к концу. Давайте вспомним, какова была цель нашего занятия. Как вы думаете, мы достигли этой цели?

- Сегодня мы познакомились с  формулами приведения, позволяющие  выразить синус, косинус, тангенс и котангенс углов вида:  ,,, где 0<α<π/2, через угол α.

На следующих уроках нам потребуется умение находить синусы, косинусы, тангенсы углов больших 900, не только на уроках алгебры , но и на уроках  физики.

Я благодарю вас за урок. Вы подарили мне хорошее настроение, я надеюсь, что я вам тоже.

Выставление оценок.

Скачано с www.znanio.ru