Формулы синуса, косинуса и тангенса половинного угла.

Синус, косинус и тангенс половинного угла.

I.                 Вывод учащимися формул половинного угла.

План вывода формул:

1. Выписать формулу  косинуса двойного угла cos 2x =…  и основное тригонометрическое тождество cos ² x + sin² x =…

2. В этих формулах заменить угол х на угол   

получим формулы cos α = cos²  - … и   1=sin²  + …

3.  а)  сложить эти два равенства;

получить выражение 1 + cos α = …Выразить из этой формулы cos²  = …

     б)  вычесть из основного тригонометрического тождества 

формулу  cos α = cos²  -…

получить выражение 1 - cos α = … Выразить из этой формулы sin²  =…

4. По определению тангенса  получить tg ²  …

II. Выписать в тетрадь полученные формулы:

1.  sin² =…

2.  cos²

3.  tg ²

4.  tg ²

5.  tg ²

III.Решение примеров на полученные формулы.

Пример 1. Вычислить sin ,  если sin α= -   α

Решение.

Sin  = ± 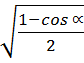;  cos α =± α- находится в IV четверти

cos α >0   cos α = ; угол  находится вo II четверти    Sin  = 

                                                                                Ответ: 0,5

Пример 2. Вычислить  3 + 6 cos²   cos α =

Решение.

cos² ;    cos² ;    3 + 6˔ =7.      Ответ: 7.

Пример 3. Вычислить  tg cos α = ; α

Решение.

α; угол α находится в III четверти, тогда угол  находится во II четверти.

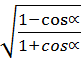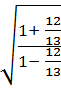 tg  = -   tg  = -  = - = -5.

                                                                                                Ответ:  -5.

Домашнее задание.

Упростить и вычислить:

1. 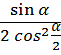      при  cos α= -0,5

2.        при

3.    при

4.    + 2cos ² α

5.          при α =

6.     -