Функции.

Функции.

Часто при разработке программ возникает ситуация, когда в разных частях создаваемой программы приходится выполнять одни и те же действия. Нередко бывает, что аналогичные действия нужно выполнять и в разных программах. К числу таких действий относится возведение числа в квадрат, извлечение квадратного корня, определение модуля (абсолютной величины) числа, вычисление тригонометрических функций, округление дробного числа до ближайшего целого, определение длины строковой переменной и другие.

Для того, чтобы облегчить процесс составления программ в языке Паскаль предусмотрены специальные функции, которые используются для автоматического выполнения этих действий. Такие функции называются стандартными и являются неотъемлемой частью языка Паскаль.

Каждая из этих функций по вводимым в нее исходным данным, определяет некоторый, результат, который далее используется в программе.

Исходные данные называются аргументом функции, а вычисленный результат

–   ее значением. При обращении к функции аргумент указывается в скобках.

К наиболее широко употребляемым стандартным функциям помимо уже известных нам функций length, ord и char, используемых для работы со строковыми переменными, относятся также следующие:

abs(x) – определяет aбсолютное значение аргумента, которым может быть число или выражение целого или вещественного типа.

arctan(x) – вычисляет арктангенс угла, значение которого выражено в радианах.

cos(x) – вычисляет косинус угла, значение которого выражено в радианах.

exp(x) – вычисляет экспоненту аргумента (то есть e в степени x).

ln(x) – вычисляет натуральный логарифм аргумента (т. е. логарифм по основанию e).

sin(x) - вычисляет cинус угла, значение которого выражено в радианах.

sqr(x) – вычисляет квадрат аргумента, которым может быть число или выражение целого или вещественного типа.

sqrt(x) – вычисляет квадратный корень из аргумента.

round(x) – округляет значение аргумента до ближайшего целого числа.

str(x) – преобразует числовое выражение в строку.

val(x) – преобразует строку, изображающую целое или вещественное число, в число.

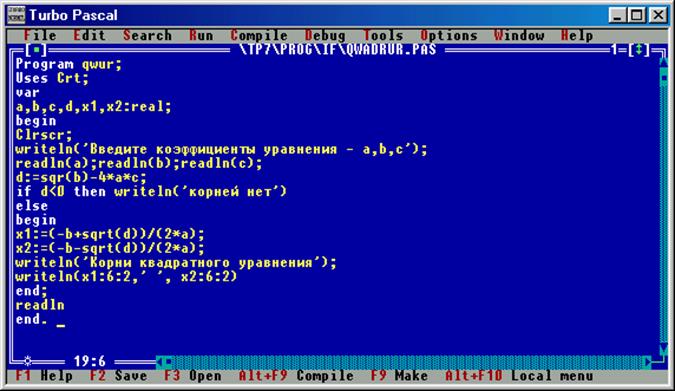
В качестве примера программы с использованием стандартных функций рассмотрим программу решения квадратичного уравнения ax²+bx+c=0 (см. рис. 25).

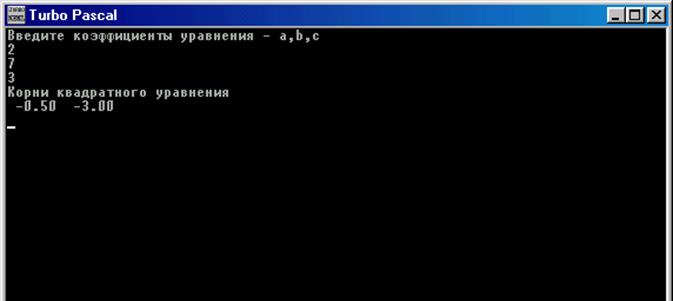Рис.   25.  Программа  решения  квадратичного  уравнения                   и результаты его решения.

В данной задаче сперва с помощью стандартной функции sqr вычисляется дискриминант уравнения. В зависимости от значения дискриминанта выясняется имеет ли данное уравнение решение. Если решения нет, то соответствующее сообщение выводится на экран компьютера. В случае же, если решение имеется, оно определяется с помощью стандартной функции sqrt.

При значениях коэффициентов уравнения 2, 7 и 3 получаем следующее решение (см. рис. 25).

Набор стандартных функций языка Паскаль достаточно обширен (он не ограничивается вышеприведенным списком), однако в ряде случаев программисту может потребоваться для решения поставленной задачи создать свою собственную функцию. Такая функция должна быть описана в тексте программы после раздела описания констант и переменных и до начала ее основной части (то есть до слова begin). Структура описания создаваемой программистом функции выглядит следующим образом:

заголовок функции;

раздел   описания      констант   и   переменных,   используемых                       внутри функции;

begin

операторы функции

end;

Теперь разберем более подробно элементы этой структуры. Общий вид заголовка функции следующий:

function имя_функции (параметры функции): тип функции;

где function – служебное слово, означающее функция; имя функции дается по тем же правилам, что и имена переменных, в скобках указываются аргументы функции, называемые ее параметрами, причем для каждого параметра обязательно должен быть указан его тип (если параметры относятся к одному типу, то они перечисляются через запятую, а после двоеточия указывается их общий тип, если же параметры относятся к разным типам, то они отделяются друг от друга точкой с запятой); после скобок обязательно указывается тип значения самой функции.

Пример заголовка функции:

function beta (x,y:integer; z:real):real;

данная функция имеет имя beta, в ней используются 3 параметра: x и y – целого типа, z – вещественного, а значение самой функции является вещественным.

Таким образом заголовок функции в целом напоминает описание переменной, но следом за заголовком в описании функции указываются оператор или группа операторов, по которым вычисляется ее значение. Эти действия записываются в виде составного оператора, который начинается со служебного слова begin и заканчивается словом end. В составном операторе могут использоваться свои, локальные переменные. Раздел описания этих переменных (для каждой из локальных переменных также должен быть указан ее тип) помещается между заголовком и составным оператором. Не забывайте о том, что в составном операторе обязательно должен быть оператор присваивания, который присваивает получившийся результат функции.

В основной части программы действия, указанные в разделе описания функции, выполняются тогда, когда необходимо найти ее значение. Для этого необходимо осуществить обращение к функции. Обращение к функции в основной части программы включает в себя имя функции и следующий за ним список параметров, заключенный в скобки. Параметры, указанные при обращении к функции, называются фактическими параметрами, а параметры указанные в описании функции – формальными. Фактические параметры должны быть того же типа, что и формальные.

Например, правая часть оператора присваивания

d:=beta(3,4, 7.5)

представляет собой обращение к функции beta, а 3, 4 и 7.5 – фактические параметры данной функции в отличие от формальных параметров х,y и z. В качестве фактических параметров функции могут выступать и константы (как в вышеприведенном примере) и переменные. Обратите внимание, что все фактические параметры перечисляются через запятую, даже если они принадлежат к разным типам.

Рассмотрим программу определения числа сочетаний из n по m. Это число определяется по следующей формуле:

ⁿ      m!(n - m)!

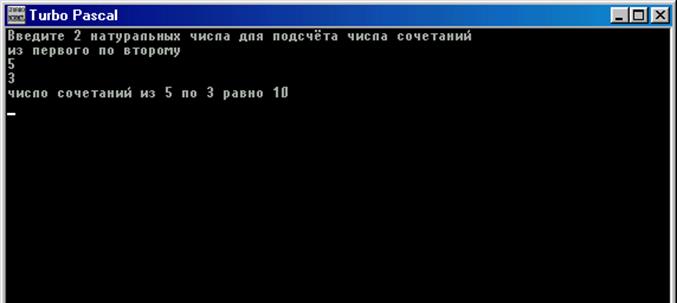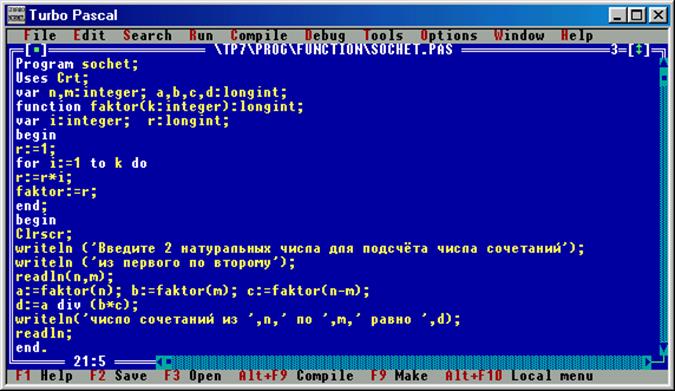
Рис.26. Программа подсчета числа сочетаний из n по m и результаты ее работы.

где   n!,m!   и   (n-m)!   –   соответственно   факториалы   n,m   и   (n-m).

Факториалом числа n называется произведение всех натуральных чисел от 1 до

n. Так как в программе нам предстоит три раза вычислять факториал различных чисел, то в целях рационализации программы вычисление факториала оформим в виде отдельной функции faktor.

Функция вычисления факториала состоит из оператора присваивания, в котором вспомогательной переменной r присваивается начальное значение 1, цикла с заданным числом повторений, в котором r последовательно умножается на числа от 1 до k и оператора присваивания, в котором функция faktor получает значение, равное конечному значению r. Так как факториалы даже небольших натуральных чисел представляют собой достаточно большие величины (например факториал числа 10 равен 3 628 800), то для описания значения функции используется тип longint.

В основной части программы осуществляется ввод исходных данных, затем производятся элементарные вычисления по формуле с использованием значений функции faktor и полученный результат выводится на экран. Ниже приведен результат работы программы при n, равном 5 и m, равном 3.

Скачано с www.znanio.ru