Функциональная грамотность на уроках математики

 «Функциональная грамотность на уроках математики»

                                                                             Составила

                                                                          учитель математики

                                                                           Гурова Валентина Николаевна

г. Конаково 2021

Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами. 

Термин «функциональная математическая грамотность» означает способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе».

 Понятие «функциональная грамотность» предполагает владение умениями:

- выявлять проблемы, возникающие в окружающем мире, решаемые посредством математических знаний,

- решать их, используя математические знания и методы,

- обосновывать принятые решения путем математических суждений,

- анализировать использованные методы решения,

- интерпретировать полученные результаты с учетом поставленной задачи.

   Предмет «Математика» играет важную роль в развитии функционально грамотной личности в школе. Его содержание направлено на формирование функциональной грамотности и основных компетенций. Математика является для школьников основой всего учебного процесса, средством развития логического мышления обучающихся, воображения, интеллектуальных и творческих способностей, основным каналом социализации личности.

            Приоритетами оценивания функциональной грамотности школьников проекта PISA являются три направления — читательская грамотность, математическая и естественнонаучная грамотность.

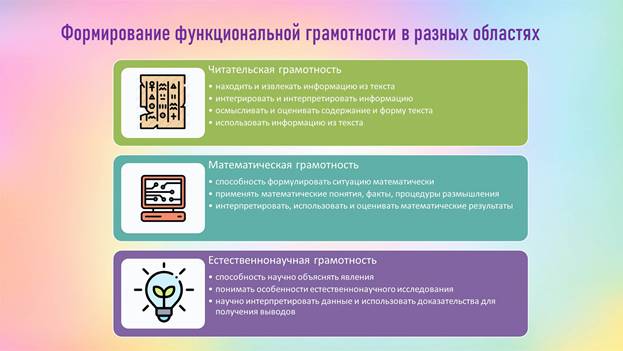
            Под «читательской грамотностью» понимается способность учащихся к осмыслению письменных текстов и рефлексии на них, использования их содержания для достижения собственных целей, развития знаний и возможностей для активного участия в жизни общества. При этом основными параметрами оценки читательской грамотности являются текст, ситуация и вопрос, так как только в совокупности они могут развивать умения не пересказа прочитанного, а поиска и интерпретации информации. В этом смысле полное понимание текста зависит от умения найти необходимую информацию и извлечь ее из общего контекста, сформулировать общее понимание текста и представить собственную точку зрения о содержании и форме текстового сообщения.

            Одно из ведущих мест в «математической грамотности» отводится учебной задаче.  Термин «учебная задача» - в широком понимании - это то, что выдвигается самим учеником для выполнения в процессе обучения в познавательных целях. Учебная задача часто рождается из проблемной ситуации, когда незнание сталкивается с чем-то новым, неизвестным, но решение учебной задачи состоит не в нахождении конкретного выхода, а в отыскании общего способа действия, принципа решения целого класса аналогичных задач. Учебная задача решается школьниками путем выполнения определенных действий: знаю – не знаю – хочу узнать.

Типы учебных задач:

• задания, в которых имеются лишние данные;

·         задания с противоречивыми данными;

• задания, в которых данных недостаточно для решения;
•  многовариативные задания (имеют несколько вариантов решения).

Задача учителя по формированию новых компетенций при работе с учащимися предполагает работу применения новых знаний, нового способа по выработанному алгоритму. Для этого учитель предлагает подросткам решить ситуационные, практико-ориентированные задания, задачи открытого типа.

Типы задач:

• Предметные задачи: в условии описывается предметная ситуация, для решения которой требуется установление и использование знаний конкретного учебного предмета, изучаемых на разных этапах и в разных его разделах; в ходе анализа условия необходимо «считать информацию», представленную в разных формах, сконструировать способ решения.
• Межпредметные задачи: в условии описана ситуация на языке одной из предметных областей с явным или неявным использованием языка другой предметной области. Для решения нужно применять знания из соответствующих областей; требуется исследование условия с точки зрения выделенных предметных областей, а также поиск недостающих данных, причем решение и ответ могут зависеть от исходных данных, выбранных (найденных) самими обучающимися.
• Практико-ориентированные задачи: в условии описана такая ситуация, с которой подросток встречается в повседневной своей жизненной практике. Для решения задачи нужно мобилизовать не только теоретические знания из конкретной или разных предметных областей, но и применить знания, приобретенные из повседневного опыта самого обучающегося. Данные в задаче должны быть взяты из реальной действительности.
• Ситуационные задачи: не связаны с непосредственным повседневным опытом обучающегося, но они помогают обучающимся увидеть и понять, как и где могут быть полезны ему в будущем знания из различных предметных областей. Решение ситуационных задач стимулирует развитие познавательной мотивации.

Задания по формированию математической грамотности на уроках математики

1.       Дидактические игры на уроках математики по формированию

                                 читательской грамотности учащихся

1. В начале урока можно предложить игру «Банк идей (гипотез)», куда ученики «складывают» свои мысли о том, что будет сегодня на уроке изучаться. Этот прием научит учеников выдвигать гипотезы исследования и определять, доказаны они или опровергнуты, что очень важно для формирования навыков научно-исследовательской деятельности учащихся при работе с литературой.

2. «Верные или неверные утверждения», или «Верите ли Вы?» может быть началом урока, когда учащиеся, выбирая «верные утверждения» из предложенных учителем, описывают заданную тему. После знакомства с основной информацией (текст параграфа, лекция по данной теме) мы возвращаемся к данным утверждениям и просим детей оценить их достоверность, используя полученную на уроке информацию.

3. Прием «План или конспект прочитанного»

Проработав доказательства теоремы, учитель может выдать каждому ученику карточку, на которой доказательство этой теоремы представлено в виде таблицы, состоящей из двух колонок, одна из которых содержит утверждения, другая — их обоснования, а также имеются пропуски в той или иной колонке. Такие карточки можно делать дифференцированными, изменив количество пропусков. Учащимся необходимо заполнить пустые места в доказательстве. Учащимся можно предложить работу с этой таблицы с использованием учебника.

2. Задания для учащихся по формированию функциональной грамотности.

5-6 класс

Задача 1.  «Геометрическая»

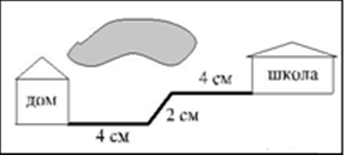
1.1. На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см:10000 см

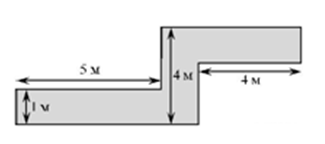
1.2. Определите, сколько необходимо закупить пленки для гидроизоляции садовой дорожки, изображенной на рисунке, если её ширина везде одинакова.

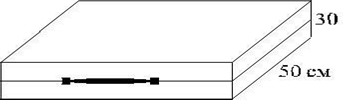
1.3.

Найдите периметр прямоугольного участка земли, площадь которого равна 800 м 2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.

1.4.

Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?

1.5.

Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см 2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).

1.6.

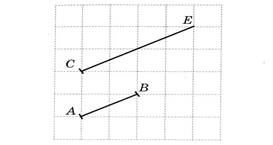
А.) Сравните длины отрезков. Сделайте вывод.

Б) Отложите от точки С отрезов, равный АВ. Можно ли это сделать. Сколько вариантов можно предложить?

В) От точки А отложите отрезок, равный СЕ. Можно ли это сделать?

Г) На каждом отрезки отметьте его середину. Сравните половину отрезка СЕ и отрезок АВ. Сделайте вывод.

1.7. Расположите номера длин отрезков в порядке возрастания.

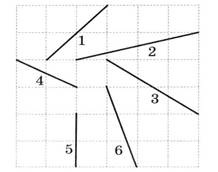
А) Придумайте и задайте вопросы своему однокласснику. Какие выводы можно сделать по итогам решения задачи?

Б) Изобразите отрезок, равный сумме отрезков №4 и № 5. Найдите его середину. Чему равна длина этого отрезка? Чему равна длины половины этого отрезка?

В) Изобразите отрезок, длина которого равна разности отрезков №6 и №5. Вычислите длину этого отрезка.

7-8 класс

Задача 2. «Ибупрофен».

Семья состоит из четырёх человек, мама и сын заболели. Надо купить лекарство, чтобы вылечить указанных членов  семьи, но лечение необходимо проводить всем членам семьи. Прежде чем купить выписанное врачом лекарство, надо прочитать инструкцию. Если противопоказания не принесут вред здоровью членам семьи, то нужно просчитать сколько упаковок данного лекарства нужно купить в аптеке. Для этого нужно знать вес членов семьи. Мама весит 65,8 кг, папа 96,3 кг, бабушка 85,6 кг, а малыш весит 9,5 кг.

А) Сколько нужно купить упаковок на всю семью, если курс лечения составляет 4 дня,

Б) Сделайте расчет, если ребенок не хочет принимать таблетки?

В) Какую сумму нужно потратить на покупку лекарства?

Г) Какую сумму нужно потратить на покупку лекарства, если в аптеке акция: при покупке двух упаковок таблеток на вторую 15% скидки.

Задача 3. «Проценты».

3.1. Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?

3.2. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?

3.3. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма в рублях из этой прибыли должна пойти на выплату частным акционерам?

3.4. В понедельник некоторый товар поступил в продажу по цене 1000 р. В соответствии с принятыми в магазине правилами цена товара в течение недели остается неизменной, а в первый день каждой следующей недели снижается на 20% от предыдущей цены. Сколько рублей будет стоить товар на двенадцатый день после поступления в продажу?

3.5. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек?

3.6. Суточная норма потребления витамина С для взрослого человека составляет 60 мг. Один помидор в среднем содержит 17 мг витамина С. Сколько процентов суточной нормы витамина С получил человек, съевший один помидор? Ответ округлите до целых.

8-9 класс

Задача 4. «Теорема Пифагора, признаки подобия и другое»

4.1. Мальчик прошел от дома по направлению на восток  метров. Затем повернул на север и прошел  метров. На каком расстоянии от дома оказался мальчик?

4.2.  В  метрах одна от другой растут две сосны. Высота одной  метр, а другой -  метров. Найдите расстояние между их верхушками.

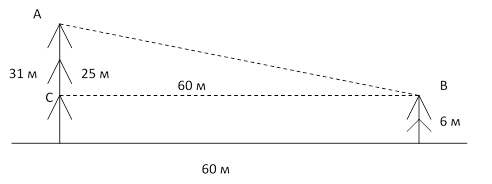
4.3. Длина тени фабричной трубы равна м; в это же время вертикально воткнутый в землю кол высотой  м дает тень длиной  м. Найдите высоту трубы.

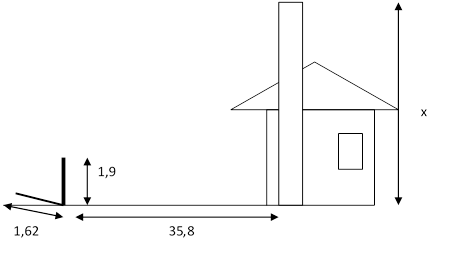
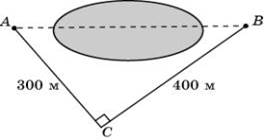
4.4. Используя данные, приведенные на рисунке, найдите расстояние в метрах между пунктами А и В, расположенными на разных берегах озера.

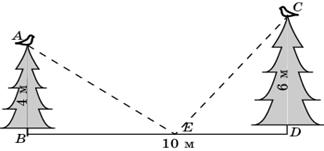
4.5.  На вершинах двух елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно 10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковыми?  

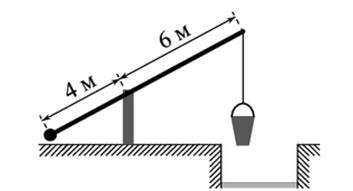
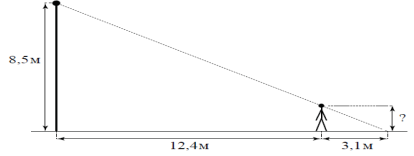
4.7.  Человек стоит на расстоянии 12,4 м от столба, на котором висит фонарь, расположенный на высоте 8,5 м. Длина тени человека равна 3,1 м. Какого роста человек (в метра)?

Задача 5. Задания с научными текстами:

 оценка вычислений при решении практических задач.

5.1.  Про­чти­те текст.

Масса самой боль­шой пла­не­ты Сол­неч­ной си­сте­мы — Юпи­те­ра — в 318 раз боль­ше массы Земли. Во­круг мно­гих пла­нет дви­жут­ся их спут­ни­ки, ко­то­рые также удер­жи­ва­ют­ся вб­ли­зи пла­нет си­ла­ми тя­го­те­ния. Спут­ник нашей Земли — Луна — самое близ­кое к нам не­бес­ное тело. Рас­сто­я­ние между Луной и Землёй равно в сред­нем 380 000 км. Масса Луны в 81 раз мень­ше массы Земли.

Чем мень­ше масса пла­не­ты, тем с мень­шей силой она при­тя­ги­ва­ет к себе тела. Сила тя­же­сти на по­верх­но­сти Луны в 6 раз мень­ше силы тя­же­сти, дей­ству­ю­щей на по­верх­но­сти Земли. На­при­мер, ав­то­мо­биль, масса ко­то­ро­го 600 кг, на Луне весил бы не 6000 Н, как на Земле, а 1000 Н, что со­от­вет­ству­ет 100 кг на Земле. Чтобы по­ки­нуть Луну, тела долж­ны иметь ско­рость не 11 км/с, как на Земле, а 2,4 км/с. А если бы че­ло­век вы­са­дил­ся на Юпи­тер, масса ко­то­ро­го во много раз боль­ше массы Земли, то там он весил бы почти в 3 раза боль­ше, чем на Земле.

Сможет ли семиклассник поднять на Земле предмет, который весит на Луне 60Н? Ответ объясните.

5.2. Прочтите текст.

Байкал — самое глубокое озеро на планете. Наибольшая глубина Байкала — 1642 метра. Байкал находится в Сибири между Иркутской областью и Республикой Бурятия. Живописные берега озера тянутся на 2000 километров, а площадь водной поверхности составляет 31 722 кв. км. Прибрежные территории отличаются уникальным разнообразием флоры и фауны. Вода в Байкале удивительно прозрачна: видно дно на глубине 40 метров. Запасы пресной воды в Байкале огромны: объём озера — 23 615 куб. км. Байкал является частью огромной экологической системы, охватывающей сотни тысяч квадратных километров. Специалисты считают, что снижение уровня воды в Байкале даже на 10 см приведёт к необратимым катастрофическим последствиям для всей Восточной Сибири. Есть план построить на берегу озера завод, который будет выпускать байкальскую воду в бутылках. Экологи сильно обеспокоены сложившейся ситуацией.

Предположим, что завод будет выпускать 20 миллионов 5-ых бутылок в год. Будет ли заметно понижение уровня воды в Байкале, вызванное деятельностью завода в течение трех лет? Ответ обоснуйте.

5.3  Прочтите текст.

В 1654 г. Отто Герике в г. Магдебурге, чтобы доказать существование атмосферного давления, провёл такой опыт. Он выкачал воздух из полости между двумя металлическими полушариями, сложенными вместе. Давление атмосферы так сильно прижало полушария друг к другу, что их не могли разорвать восемь пар лошадей. Силу F (в ньютонах), сжимающую полушария, вычисляют по формуле F = P · S, где P — давление в паскалях, S  — площадь в квадратных метрах. В опыте Отто Герике атмосферное атмосферное давление составляло 760 мм ртутного столба и действовало на площадь, равную 0,28 м². Известно, что 1 мм рт. ст. = 133 Па. С высотой давление атмосферы уменьшается на 1 мм рт. ст. при подъеме на каждые 12 метров. Это явление позволяет измерять высоту объектов приборами, называемыми высотометрами.

Значительно ли измениться сжимающая сила, действующая на магдебургские полушария, если опыт Герике проделать на 240 метров выше? ( Значительным изменением будем считать изменение более, чем 10 1%).

5.4. Прочтите текст.

Калория — количество теплоты, необходимое для нагревания 1 грамма воды на 1 градус Цельсия при стандартном атмосферном давлении. Калория (обозначается: кал) может быть выражена в джоулях: 1 кал = 4,1868 Дж точно, 1000 калорий обозначается ккал. Калория применяется при оценках энергетической ценности («калорийности») пищевых продуктов. На упаковках пищевой продукции, продаваемая на территории Российской Федерации и многих других стран мира, обязательно указывается ее энергетическая ценность.

Екатерина Молокова на каникулах посещала г.Пятигорск. перед тем как выйти из дома, она позавтракала следующими блюдами и напитками: омлет с ветчиной, овощной салат, картофель по-деревенски и чай с сахаром (две чайные ложки). Сначала Екатерина решила сходить на экскурсию по парку протяженностью 1,5 км, а потом посетить 10-этажную старинную башню. На прогулке девушка шла со скоростью 1м/с и тратила по 150 ккал/час. При подъеме или спуске на 1 этаж тратится 6,5 ккал. Используя данные таблицы, определите, истратила ли Екатерина всю энергию, которую получила на завтраке?

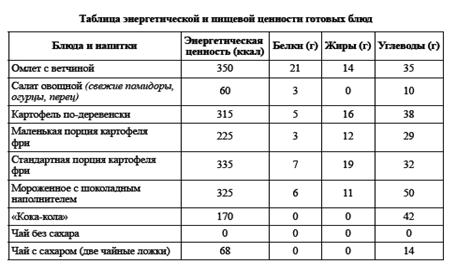
Для формирования информационной компетентности необходимо использовать задачи содержащие информацию, представленную в различной форме (таблицах, диаграммах, графиках и т.д.). Вопрос задачи может быть сформулирован следующим образом: переведите в графическую (словесную) форму; если возможно, хотя бы приближенно опишите их математической формулой; сделайте вывод, наблюдается ли в этих данных какая-то закономерность и др.

Примером такого задания может быть

Задача 5.5. Аральское море — бессточное солёное озеро в Средней Азии, на границе Казахстана и Узбекистана.

           Если  обратиться к истории Арала, то море уже высыхало, при этом снова возвращаясь в прежние берега. Итак, каким же был Арал несколько последних столетий и как менялись его размеры?

 В историческую эпоху происходили существенные колебания уровня Аральского моря. В 1950-х годах Аральское море было четвёртым по площади озером мира, занимая около 68 тыс. км; его длина составляла 426 км, ширина — 284 км, наибольшая глубина — 68 м.  Объем Большого Арала и  соленость воды рассмотри в таблице.

Рассчитай а) на сколько процентов снизился объём Арала? б) На сколько процентов возросла концентрация воды в море? в)  Камбала может жить в морской воде с концентрацией не выше 40%. Водится ли сейчас в Арале камбала?

Заполни пустые клетки в таблице.                                                                                   

Задания: «Работа с текстом в таблицах».

Работа с таблицами повышает уровень наглядности изложения, позволяет учащимся анализировать более широкий ряд вариаций одного и того же процесса, отслеживать динамику развития явления при различных условиях его протекания, дает в итоге возможность получать более полную информацию по изучаемому вопросу и соответственно более глубоко усваивать учебный материал.

Информа́ция (от лат. informātiō — «разъяснение, представление, понятие о ч.-л.», от лат. informare — «придавать вид, форму, обучать; мыслить, воображать») — сведения, независимо от формы их представления, воспринимаемые человеком или специальными устройствами как отражение фактов материального мира в процессе коммуникации.

Понятие «информация» является общенаучным, используется в информатике, физике, кибернетике, биологии и др. науках. Например, в физике рассматривается мера сложности и упорядоченности системы, антиэнтропия или энтропия с обратным знаком. В биологии информация связывается с целесообразным поведением животных, используется в связи с исследованиями механизмов наследственности. В кибернетике информация связана с процессами управления в сложных системах (живых организмах или технических устройствах).

В математике информация - это общее наименование фундаментальных понятий в информатике, теории информации, кибернетике, а также в математической статистике, в которых обобщённое интуитивное представление об информации относительно каких-либо величин или явлений конкретизируется и формализуется.

Первая группа заданий формирует у учащихся навыки работы с таблицей, в процессе изучения данных - отвечать на вопросы, формулировать вопросы оппоненту.

Задача 6.1. «Таблицы и диаграммы»

В таблице представлены цены (в рублях) на некоторые товары в трёх магазинах:

Лариса Кузьминична хочет купить 0,4 кг орехов, 5 плиток шоколада и 1,5 кг зефира. В каком магазине стоимость такой покупки будет наименьшей, если в «Камее» проходит акция: скидка 20% на орехи и зефир, а в «Машеньке» скидка 10% на все продукты?

В ответе укажите номер правильного варианта.

1) В «Машеньке»

2) В «Лидии»

3) В «Камее»

4) Во всех магазинах стоимость покупки будет одинаковой

Задача 6.2. Для квартиры площадью 75 кв. м заказан натяжной потолок белого цвета. Стоимость работ по установке натяжных потолков приведена в таблице.

Какова стоимость заказа, если действует сезонная скидка в 5%?

В ответе укажите номер правильного варианта.

1) 4275 рублей    2) 45 000 рублей    3) 42 750 рублей   4) 44 995 рублей

Задача 6.3.

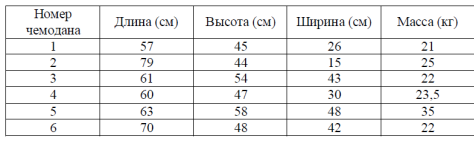
В таблице приведены данные о шести чемоданах. По правилам авиакомпании сумма трех измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 158 см, а масса не должна превышать 23 кг. Какие чемоданы можно сдать в багаж по правилам авиакомпании? В ответе укажите номера всех выбранных чемоданов без пробелов, запятых и других символов.

Задача 6.4.

Турист хочет посетить 4 музея в Санкт-Петербурге: Эрмитаж, Русский музей, Петропавловскую крепость и Исаакиевский собор. Экскурсионное бюро предлагает маршруты с посещением одного или нескольких объектов. Сведения о стоимости билетов и составе маршрутов представлены в таблице.

Какие маршруты должен выбрать путешественник, чтобы посетить все четыре музея и затратить на все билеты наименьшую сумму? В ответе укажите ровно один вариант номеров маршрутов без пробелов, запятых и других символов.

Финансовая грамотность

В 2016 году пробел образовательной программы школьников устранен – в российских школах ввели уроки финансовой грамотности, в ходе которых детей не только научат бережно обращаться с деньгами, но и расскажут, как можно и нужно отстаивать свои права в случае необходимости.

Главной задачей введения обучения финансовой грамотности, конечно же, является стремление остановить развитие безответственного отношения к денежным операциям в целом. Ведь большая часть взрослого населения нашей страны, к сожалению, до сих пор финансово безграмотна и ничем не защищена.

Школьный курс финансовой грамотности охватывает следующие понятия и темы:

• составление и расчет семейного бюджета;
• денежные операции в банках и других структурах;
• сделки, связанные с риском;
• денежные вознаграждения;
• наличие ответственных органов за финансовые услуги;
• личные сбережения — излишество или прок;
• тонкости кредитов и депозитов;
• права и обязанности участников финансово-экономических отношений;
• управление денежными потоками;
• агрессивная политика банков;
• активы и пассивы (доходы и расходы);
• страхование и пенсионные выплаты;
• наличие и безопасное использование пластиковых карт.

Что же такое финансовая грамотность?

О.Е. Кузина[3] Финансовая грамотность – это знания и навыки в области финансов, которые должны применяться в повседневной жизни и приносить положительные финансовые результаты.

Несколько задач по формированию финансовой грамотности

Задача 1

Вы- студент и получаете стипендию в размере 3000 рублей. Через три месяца у друга день рождения. Вы хотите накопить и сделать ему подарок. Ежемесячно вы тратите на проезд 380 рублей, на поход в кино – 950 рублей, на оплату телефона – 300 рублей. Выберите самый выгодный инструмент достижения вашей цели:

А. Открыть пополняемый депозит без капитализации процентов под 10% годовых.

Б. Открыть пополняемый депозит с ежемесячной капитализацией процентов под 9,5% годовых.

Решение:

1.      Определим величину свободных денег (СД), предназначенных на накопление:

СД=3000-380-950-300=1370 рублей

2.      Определим какой из вкладов является более доходным.

а) Формула расчёта наращенной суммы вклада при простом начислении процентов определяется по формуле:

SUM=X *(1+p*d/B), где

Х – начальная сумма вклада;

Р - процентная ставка по вкладу (годовая)/100;

d – количество дней в периоде;

В – количество дней в году

SUM = 1370х(1+0,1х3/12)=1404,25

б) Формула расчёта наращенной суммы вклада при сложном начислении процентов несколько раз в год определяется по формуле:

SUM=X *(1+p*d/B)ͫ , где

Х – начальная сумма вклада;

Р - процентная ставка по вкладу (годовая)/100;

d – количество дней в периоде;

В – количество дней в году

m- количество периодов, в которых осуществляется капитализация

SUM= 1370х(1+0,095х1/12)³=1370х1,00792³=1370 х 1,0239=1402,7 р.

Таким образом, выбираем вариант с размещением денег на пополняемый депозит под 10% годовых, т.к. он более доходный

Задача 2

Заполните таблицу месячного бюджета семьи и рассчитайте семейные накопления. Месячные доходы и расходы семьи следующие: начисленная зарплата отца составляет 57000 руб.; начисленная зарплата матери – 42000 руб.; начисленная зарплата старшего сына – 28000 руб.; коммунальные платежи – 9700 руб.; на обеды во время работы семья тратит 15800 руб.; питание дома – 24300 руб.; расходы на одежду, обувь – 9300 руб.; проезд в общественном транспорте – 3900 руб.; бытовые расходы – 7100 руб.; развлечения, отдых – 14200 руб.; эксплуатация автомобиля – 9900 руб.; ежемесячные платежи по кредиту за мебель – 5500 руб.; ежемесячный перевод бабушке, живущей в другом городе, – 7500 руб.; прочие расходы – 2200 рублей.

Решение:

1)      Определим выданную на руки зарплату отца

57000 × 0,87 = 49590 рублей.

2) Определяем выданную на руки зарплату матери:

42000 × 0,87 = 36540 рублей.

3) Определяем выданную на руки зарплату сына:

28000 × 0,87 = 24360 рублей.

4) накопления семьи составили:

Ответ: 1090 рублей.

Задача 3

В небольшом городе, где живет Алексей, интернет-магазины не отличаются высокой обязательностью. Так, вероятность того, что нужный товар доставят из магазина «Электроник», составляет 0,7, а из магазина «Интернет +» – 0,85. Молодой человек заказал необходимый товар сразу в двух магазинах. Определите вероятность того, что

ни один магазин не доставит товар. Считать, что интернет-магазины работают независимо друг от друга.

Решение.

Вероятность того, что первый магазин не доставит товар, равна

1 − 0,7 = 0,3.

Вероятность того, что второй магазин не доставит товар, равна 1 − 0,85 = 0,15.

Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,3 · 0,15 = 0,045.

Ответ: 0,045.

Задача 4.

Николай планирует в конце года купить новый автомобиль. Определите, какой комплектации автомобиль может купить Николай, если его начисленная заработная плата равнялась 100 000 руб. в месяц. Личные накопления Николая на начало года составляли

500 000 руб., а постоянные ежемесячные расходы – 25 000 рублей. Николай оплатил следующие налоги:

1 – за квартиру, находящуюся в собственности (единственная) площадью 62 м2 кадастровой стоимостью 8 600 000 руб. по налоговой ставке 0,1%;

2 – за автомобиль с мощностью двигателя 105 лошадиных сил (л.с.) по налоговой ставке 25 руб. за 1 л.с.

Николай выбирает новый автомобиль в следующих комплектациях:

1. Комплектация стоимостью 1 150 000 рублей,

2. Комплектация стоимостью 1 350 000 рублей,

3. Комплектация стоимостью 1 420 000 рублей.

Дополнительная информация.

Налог на имущество физических лиц, исходя из кадастровой стоимости объекта, рассчитывается по следующей формуле:

Нк= (КС– НВ) ×НС

где: КС – кадастровая стоимость;

НВ – налоговый вычет;

НС – налоговая ставка.

НВ=КС1 ×S,

где: КС1 – кадастровая стоимость одного метра недвижимости;

S – жилплощадь, не облагаемая налогом (для квартиры она составляет 20 м2).

Транспортный налог определяется как:

Нт = НС ×Nл.с.,

где Nл.с. – мощность двигателя автомобиля в лошадиных силах.

Решение.

1) Рассчитаем выданную заработную плату, которую получит Николай за год (после уплаты НДФЛ)

100 000 × 12 × 0,87 = 1 044 000 руб.

2) Общие доходы Николая за год:

1 044 000 + 500 000 = 1 544 000 рублей.

3) Постоянные расходы Николая за год равны:

25 000 × 12 = 300 000 руб.

4) Рассчитаем налог, который заплатит Николай за квартиру.

Кадастровая стоимость 1 м2 квартиры будет равна:

8 600 000 : 62 = 138 709,68 рублей.

Найдем кадастровую стоимость жилплощади, не облагаемой налогом:

138 709, 68 × 20 = 2 774 193, 60 руб.

Кадастровая стоимость части квартиры, облагаемой налогом на недвижимость:

8 600 000 – 2 774 193, 60 = 5 825 806, 40 руб.

Налог на квартиру равен:

5 825 806, 40 × 0, 001 = 5825,81 рублей.

5) Рассчитаем транспортный налог

105 × 25 = 2625 рублей.

6) Рассчитаем денежную сумму, которая останется у Николая на конец года:

1 044 000 + 500 000 – 300 000 - 5825,81 - 2625 = 1 235 549,19 руб.

Таким образом, Николай может купить новый автомобиль только в комплектации 1.

Ответ: Комплекция 1.

Задача 5

Банк «Дружба» предлагает жителям города Энск два варианта депозита для разных категорий горожан:

1) Для молодых семей и студентов депозит под 8% с начислением процентов ежемесячно;

2) Для всех других горожан – депозит под 8% с начислением процентов в конце года.

Определите более выгодный вариант размещения депозитов на один год.

Решение.

Более выгодным считается тот вариант, при котором наращенная за год сумма будет больше. Для оценки вариантов начальную сумму примем равную 5 000 руб.

1) По первому варианту проценты начисляются ежемесячно:

Sn= S0 ∙ (1 + 0,01р/12)q, где q – количество месяцев, p – процентная ставка по депозиту,

S0 – начальная сумма.

S12 = 5 000 ×∙ (1+0,08/12)12 = 5000 ×∙ (1 + 0,0067)12 = 5000 ×1,006712 = 5417,15 рублей.

2) По второму варианту накопленная сумма будет равна:

(1+0,08) ×· 5000 руб.= 5400 рублей.

Расчёты показывают, что молодым семьям и студентам открывать подобный вклад выгоднее при условии применения сложных процентов

Ответ: вариант 1

Задача 6

Девушка положила на депозит некоторую сумму денег. Через два года

 сумма достигла 114 490 руб.

Каков был первоначальный вклад при 7% годовых? Какова прибыль, если вклад с ежегодной капитализацией процентов?

Решение.

n = 2; р = 7%; S2= 14 490; S0= ?

Находим Sо по формуле: Sо = Sn · (1 + 0,01р)ͫ

S2 = S0∙(1 + 0,07) ²

114 490 =S0∙(1,07) ², S0=114 490 : 1,1449 = 100 000 рублей – первоначально.

Прибыль: 114 490 – 100 000 = 14 490 рублей.

Ответ: 100 000 рублей, 14 490 рублей.

Зачем нужна финансовая грамотность

Однако уроки финансовой грамотности очень важны и как нельзя актуальны в современных российских условиях. Нынешние российские школьники уже активно пользуются "благами" капитализма – покупают товары, пользуются пластиковыми картами и мобильными приложениями. Они уже с довольно раннего возраста переходят в категорию потребителей. Умение пользоваться деньгами для них уже крайне важно, так как именно детский мозг больше всего подвержен влиянию рекламы, и транснациональные корпорации уже вовсю наживаются на детях и подростках. Еще одна важная причина для внедрения финансовой грамотности в школах – это развитие навыка по выявлению реальных потребностей и отделения их от сиюминутных желаний. Наверняка многие из нас видели бьющихся в истерике детей в супермаркетах или школьников, увешанных гаджетами. Эти дети не знают, что деньги – это результат тяжелого труда родителей. Они привыкли к тому, что всегда получают все, что хотят. Родители воспринимаются как аналог бездонного кошелька. Главное, что должны донести до детей занятия по финансовой грамотности – деньги нужно зарабатывать и уметь тратить так, чтобы они принесли максимальную пользу, а не сиюминутное удовлетворение.

Однако проблема финансовой грамотности детей не может быть решена без повышения финансовой грамотности педагогов и родителей.

Должна быть организована просветительская работа с родителями в форме видео-семинаров, тематических бесед и родительских собраний.

Для всего этого в Министерстве науки и образования необходимо разработать специальные программы и стандарты.

Помимо вышесказанного рекомендуется организовать не просто центры переподготовки педагогов, но и проводить профессиональное обучение педагогического состава школ простейшим навыкам по работе с финансами. При этом главное, что должно быть донесено до педагогов, большинство из которых сидят на кредитной игле, жалуясь при этом на низкую зарплату: "Траты не должны превышать заработок". Если зарплата не покрывает потребности, нужно развиваться и расти профессионально, а именно получать категорию, повышать квалификацию, подрабатывать репетиторством или же разрабатывать собственные образовательные или учебные курсы. Только работа на уровне всех слоев общества вкупе с адекватной пропагандой финансовой грамотности способна преодолеть опасность растущей кредитной зависимости в обществе и повысить благосостояние населения.

Литература

1.      Белехова Г.В. К вопросу о финансовой грамотности населения // Журнал: Проблемы развития территории – Издательство: Вологодский научный центр Российской академии наук (Вологда)

2.      Шевяков М.Ю. Перспективы изменения финансового поведения в результате повышения уровня финансовой грамотности // Бюджет и финансы: финансовая грамотность.- 2011. – No1 (10-11). – С.30-35. Овчинников М. Обзор международной практики реализации стратегий и программ в области финансовой грамотности – М.: 2008

3.      Кузина О. Финансовая грамотность и финансовая компетентность: определение, методики измерения и результаты анализа в России // Вопросы экономики. 2015. № 8. С. 129-148

4.      Доклад о финансовой грамотности, PISA 2012 Александра Воздвиженская Поле чудес. В школах введены уроки финансовой грамотности // URL: https://rg.ru/2016/09/07/v-shkolah-vveli-uroki-finansovoj-gramotnosti.html
Калинкина Е.Н. Сборник заданий по развитию функциональной математической грамотности обучающихся 5-9 классов.-Новокуйбышевск, 2019.

5. Развитие функциональной грамотности обучающихся  основной школы: методическое пособие для педагогов /Под общей редакцией Л.Ю. Панариной, И.В. Сорокиной, О.А. Смагиной, Е.А. Зайцевой. – Самара: СИПКРО, 2019. - с.

Скачано с www.znanio.ru