Конформные отображения, определяемые комбинациями основных элементарных функций

Функция Жуковского

Определение 8. Функция

называется функцией Жуковского. Эта функция аналитична в точках z ≠ 0, ∞, причем

однолистна, в частности, в следующих областях:

а) |z| >1 – внешность единичного круга,

б) |z| < 1 – единичный круг,

в) Im(z) > 0 – верхняя полуплоскость,

г) Im(z) < 0 – нижняя полуплоскость.

Положив в (7) z = re^iϕ, w = u + iv, получим

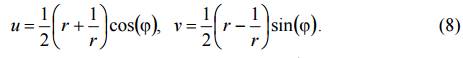
Отсюда следует, что образом окружности z = pe^iϕ (0 ≤ ϕ ≤ 2π, p > 0 – фиксировано) является эллипс

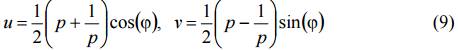
с полуосями

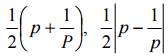
и с фокусами в точках w = ±1.

Исключая из уравнений (9) параметр ϕ при  p ≠ 1, получим уравнение эллипса в каноническом виде

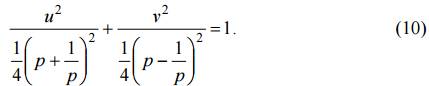
При замене р на 1/p (p ≠1) эллипс (10) остается тем же самым, но его ориентация меняется на противоположную.

Таким образом, окружности |z| = p, p >1, ориентированные по часовой стрелке, переходят в эллипсы (10), ориентированные также по часовой стрелке. При отображении окружностей |z| = p, 0 < p < 1 ориентация меняется на противоположную.

При p = 1 эллипс (9) вырождается в отрезок  [−1, 1], проходимый дважды, т.е. окружность |z| =1 переходит в отрезок  [−1, 1], проходимый дважды. Таким образом, функция Жуковского конформно отображает внешность (внутренность) единичного круга на внешность отрезка [−1, 1] (рис. 3).

Из (8) следует, что образом луча z = re^iα, 0 < r < +∞ (α – фиксировано), является кривая

Исключая параметр r , при α ≠ kπ 2 ( k – целое), получаем

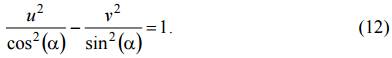
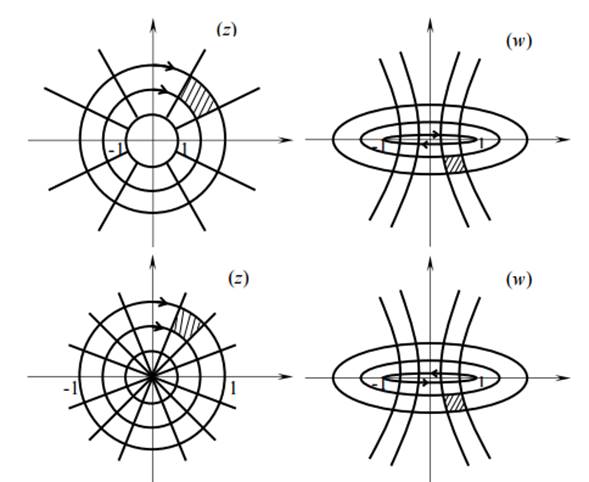
Рис. 3

Кривая (12) – гипербола с фокусами в точках  w = ± 1 и с асимптотами v = ±u⋅tg(α). Если 0 < α < π/2, то кривая (11) является правой ветвью гиперболы (12), т.е. луч r = re^iα, 0 < α < π/2 переходит в правую ветвь гиперболы (ориентация показана на рис. 4), при  π/2 – < α < π в левую ветвь (в (11) заменяем α на π − α ). При замене в (11) α на − α получаем ту же ветвь гиперболы, но с противоположной ориентацией. При α = 0 (луч arg (z) = 0) кривая (11) вырождается в луч [1, +∞), проходимый дважды, луч arg (z) = π переходит в луч  [− ∞,−1], проходимый дважды, лучи arg(z) = π/2 и arg(z) = 3π/2 переходят в мнимую ось Re(w) = 0. Отсюда следует, что функция Жуковского конформно отображает верхнюю полуплоскость Im(z) > 0 на плоскость w с разрезами по лучам [ − ∞,−1] и [ 1 ,+∞] (аналогично нижнюю полуплоскость Im(z) < 0).

Любой эллипс (10) пересекается с любой гиперболой (12) под прямым углом.

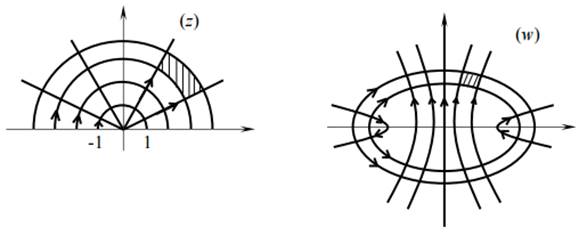
Рис. 4

Функция w = z +  − является обратной к функции Жуковского, она аналитична в плоскости z с выколотыми точками z = ±1, а в плоскости z с разрезом, соединяющим точки 1 z = ± , распадается на две регулярные ветви f₁(z) и f₂(z) , где f₁(∞) = ∞, f₂(∞) = 0.  Из свойств функции Жуковского следует, что функция w = f₁(z) конформно отображает плоскость z с разрезом по отрезку [−1, 1]на внешность единичного круга, а функция w = f₂(z)  – на круг |w| < 1.

Скачано с www.znanio.ru