Функція корисності споживача

ФУНКЦІЯ КОРИСНОСТІ СПОЖИВАЧА

Рішення споживача щодо купівлі певного набору товарів математично можна подати як вибір точки у просторі товарів. Нехай
n — скінченне число видів різноманітних товарів,

де D_i – обсяг товару i-го виду,

           - вектор-стовпець споживчих товарів (обсяги), що їх придбав споживач за певний термін (наприклад протягом року) за заданих цін, маючи певний обсяг доходу за цей самий період.

           Це означає, що для кожної пари  товарів має місце одне з трьох відношень, :

   — набір  є привабливішим, ніж ;

  — набір  є менш привабливим, ніж ;

 ~  — для споживача обидва набори еквівалентні.

         Переваги споживача можна подати у фор­мі індикатора переваг, тобто такої функції корисності

, ,

що з    випливає ,

з   випливає ,

з  ~  випливає .

          Уведення функції корисності дозволяє замінити відношення переваги звичними відношеннями між числами: більше, менше, дорівнює.

       У теорії споживання припускаються гіпотези і вважається, що функція корисності неперерва та диференційована. Вона має такі властивості:

1) 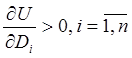 — зі зростанням споживання товару корисність зростає;

2) 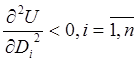  - зі зростанням споживання товару швидкість зростання корисності зменшується (спадає);

Розглянемо види функції корисності для товарів двох видів:

1) неокласична

,

2) із взаємозаміщенням

,

3) із взаємодоповненям

,

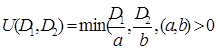4) логарифмічна

.

           Розглянемо функцію корисності для товарів n видів

.

            Гранична корисність товару

,

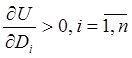показує, на скільки зростає корисність, якщо кількість товару зростає в малому обсязі.

        Гранична норма заміщення товарів показує, скільки необхідно одиниць j-го товару, щоб замінити малий обсяг і-го товару, який вибув.

.

  Припустимо, що функція корисності маї вигляд

,

де р_i – ціна одиниці товару і-го виду,

.

Знайдемо граничні корисності

,   .

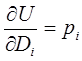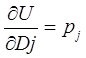Розглянемо відношення граничних корисностей

.

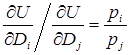Це відношення має назву 2-го  закону Госсена.