Гармонические колебания

Колебания и волны

Тема. Гармонические колебания

Цель урока: ознакомить учащихся с понятием гармонических колебаний.

Тип урока: урок изучения нового материала.

ПЛАН УРОКА

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Уравнение колебательного движения груза на пружине

Во многих колебательных системах при малых отклонений от положения равновесия модуль вращательной силы, а значит, и модуль ускорения прямо пропорционален модулю смещения относительно положения равновесия.

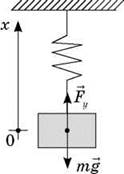
Покажем, что в таком случае смещение зависит от времени по закону косинуса (или синуса). С этой целью проанализируем колебания груза на пружине. Выберем за начало отсчета точку, в которой находится центр масс груза на пружине в положении равновесия (см. рисунок).

Если груз массой m смещен от положения равновесия на величину х (для положения равновесия х = 0), то на него действует сила упругости Fx = -kx, где k - жесткость пружины (знак «-» означает, что сила в любой момент времени направлена в сторону, противоположную смещению).

Согласно второму закону Ньютона Fx = mах. Таким образом, уравнение, описывающее движение груза имеет вид:

Обозначим ω2 = k/m. Тогда уравнение движения груза будет иметь вид:

Уравнение такого вида называется дифференциальным уравнением. Решением этого уравнения является функция:

Таким образом, за вертикального смещения груза на пружине от положения равновесия он будет совершать свободные колебания. Координата центра масс при этом изменяется по закону косинуса.

2. Гармонические колебания

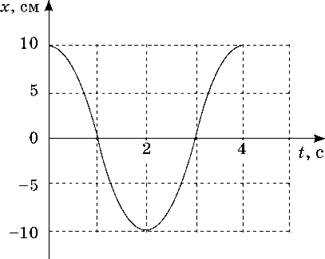
Убедиться в том, что колебания происходят по закону косинуса (или синуса) можно на опыте. Ученикам целесообразно показать запись колебательного движения (см. рисунок).

Ø Колебания, при которых смещение зависит от времени по закону косинуса (или синуса), называются гармоническими.

Свободные колебания груза на пружине представляют пример механических гармонических колебаний.

Пусть в некоторый момент времени t1 координата колеблющегося груза равна x1 = xmax cosωt1. Согласно определению периода колебаний, в момент времени t2 = t1 + T координата тела должна быть такой же, как и в момент времени t1, то есть х2 = х1:

Период функции cosωt равен 2, следовательно, ωТ = 2, или

Но поскольку Т = 1/v, то ω = 2v, то есть циклической частота колебаний ω является количество полных колебаний, совершаемых за 2 секунд.

ВОПРОС К УЧАЩИМСЯ В ХОДЕ ИЗЛОЖЕНИЯ НОВОГО МАТЕРИАЛА

Первый уровень

1. Приведите примеры гармонических колебаний.

2. Тело выполняет незатухающие колебания. Которые из величин, характеризующих это движение, постоянные, а какие меняются?

Второй уровень

Как изменяются сила, действующая на тело, его ускорение и скорость во время осуществления им гармонических колебаний?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

Учимся решать задачи

1. Напишите уравнение гармонического колебания, если его амплитуда 0,5 м, а частота 25 Гц.

2. Колебания груза на пружине описывают уравнением х = 0,1sin0,5. Определите амплитуду, круговую частоту и частоту колебаний.

3. Амплитуда колебания 2 см, смещение 1 см. Сколько времени прошло от начала колебаний?

Решение

Если бы движение было равномерным, то ответ был бы: t = 1/8Т. Но движение груза в этом задании неравномерный. Уравнение движения имеет вид: 1 = 2cosωt, откуда cosωt = 1/2. Следовательно, ωt = /3, откуда  Таким образом, t = 1/6Т.

4. Колебания описывают формулой х = 0,12sin20t. Найдите амплитуду, частоту и период колебаний.

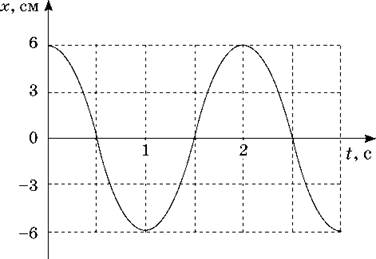
5. На рисунке приведен график гармонического колебания. Найдите амплитуду, частоту и период колебания. Запишите формулу зависимости x(t).

ЧТО МЫ УЗНАЛИ НА УРОКЕ

· Колебания, при которых смещение зависит от времени по закону косинуса (или синуса), называются гармоническими.

· Уравнение гармонических колебаний:

· Циклической частотой колебаний ω является количество полных колебаний, совершаемых за 2 секунд.

Домашнее задание

1. Подр.: § 19.

2. 3б.:

Рів1 № 10.4; 10.19.

Рів2 № 10.32; 10.33; 10.34, 10.35.

Скачано с www.znanio.ru