А. Г. ГЕйн

ИНФОРМАТИКА и икт

mai12

ЗАДАЧНИК-ППКТИКУМ

ПРОСВЕЩЕНИЕ

иноорптип и икт

Задачникпрактикум

10-11 кпссы

Базовый и профильный уровни

Москва

«Просвещение»

2010

Предисловие

Информатика принадлежит к числу быстро меняющихся дисциплин, и, хотя общие её контуры остаются сравнительно стабильными, в каждом школьном учебнике по-своему расставлены акценты. Данное пособие входит в учебно-методический комплект, разработанный коллективом авторов под руководством А. Г. Гейна. Тем не менее, создавая задачник-практикум, мы ориентировались на общие контуры предмета, очерченные в «Обязательном минимуме образования по информатике». Поэтому данная книга будет, на наш взгляд, полезна при изучении курса информатики по любому учебнику.

Весь материал разделён на разделы, соответствующие основным образовательным линиям курса; разделы делятся на параграфы, которые подразделяются на пункты. Именно для того, чтобы читателю, знакомому с курсом информатики по учебникам других авторов, было комфортно работать с данным пособием, каждый раздел, параграф, пункт открываются краткой сводкой основных определений и сведений; определяемые термины выделены жирным шрифтом. За более подробными разъяснениями в случае необходимости читатель может обратиться к одному из учебников информатики, названия которых приведены в списке рекомендуемой литературы.

Помимо собственно заданий, в книгу включены вопросы по основным теоретическим положениям школьного курса информатики — это, на наш взгляд, поможет читателю проверить себя в знании теории, которая необходима для успешного выполнения последующих заданий.

Задачник призван обслуживать как базовый, так и профильный курс информатики. Задания, относящиеся к профильному уровню, отмечены символом . Кроме того, в задачнике представлены задания разного уровня сложности. Более трудные задания помечены символом Конечно, оценка сложности задания — вещь достаточно субъективная, так что некоторые из указанных заданий могут и не показаться трудными для читателя этой книги.

Ряд заданий ориентирован на их выполнение с помощью компьютера. Такие задания помечены знаком . В основном такие задания не привязаны к какой-либо конкретной реализации средств информационных технологий.

В последнее время наблюдается тенденция переноса некоторых заданий ЕГЭ из части А (задания с выбором ответа) в часть В (задания с кратким ответом). Поэтому в нашем задачнике мы постарались предъявить не только задания,

4

аналогичные заданиям части В Единого государственного экзамена по информатике, но и возможные трансформации заданий из части А.

В конце задачника к некоторым заданиям приведены ответы. Кроме того, в заданиях, которые предусматривают использование компьютера, для некоторых исходных данных приведены результаты тестирования программ. Это позволяет читателю, самостоятельно работающему с задачником, осуществлять дополнительный контроль за правильностью выполнения заданий.

Мы надеемся, что данная книга будет полезна тем, кто изучает и преподаёт школьную информатику.

Желаем успехов!

Информация, виды информации и способы её представления

Понятие информации является первичным в информатике и не может быть строго определено в других терминах. Поэтому в информатике понятию «информация» определение не даётся, оно лишь разъясняется и иллюстрируется конкретными примерами применения данного термина. Более того, в разных разделах информатики этот термин понимается более широко или более узко в зависимости от тех проблем, которые в данном разделе рассматриваются. В S 1 приведено несколько таких толкований.

Для передачи информации или её хранения в виде того или иного сообщения требуется определённый способ кодирования. Кодирование своей главной целью имеет сохранение информации и придание ей формы, обеспечивающей полноценную (т. е. без потерь и искажений) передачу информации от источника к получателю.

Об информации, представленной последовательностью знаков, говорят, что она символьная; информация, представленная посредством какого-либо изображения, называется видеоинформацией.

8 Информация и информационные процессы

Информация — это то, что позволяет живому организму (или технической системе) адекватно реагировать на окружающую среду посредством тех или иных механизмов, индуцируя целенаправленную деятельность по сохра-

6

нению отдельного индивидуума и/или вида (системы) в целом. Такая точка зрения на понятие информации обычно принимается в тех разделах информатики, которые близки к кибернетике.

Нередко говорят, что информация — это сведения, знания об окружающем человека мире и о самом себе. Так обычно разъясняется понятие информации в гуманитарных науках, где центральным объектом является человек как существо социальное.

В теории передачи и хранения информации под информацией понимается последовательность сигналов или символов какого-либо алфавита, кодирующая некоторое сообщение без учёта смыслового содержания этого сообщения. Аналогично понимается термин «информация» и в науках, изучающих компьютерную обработку информации.

Наиболее общее понимание термина «информация» состоит в том, что информация — это отражение разнообразия в существующем мире. Отсутствие разнообразия, когда неразличимы никакие два объекта, явления или процесса, это и есть отсутствие какой бы то ни было информации.

Информацию, зафиксированную каким-либо способом, называют информационным объектом.

Информационный процесс — это процесс, в ходе которого изменяется содержание информации или форма её представления. Среди информационных процессов выделяют следующие основные виды: получение, хранение, передача, обработка, использование информации.

Получение информации — это реализация способности к отражению различных свойств объектов, явлений и процессов в окружающем мире.

Передача информации всегда осуществляется по некоторому каналу связи от источника информации к её приёмнику.

Под обработкой информации понимают любое преобразование её содержания или формы представления. Обработка информации может происходить двумя способами: формально или эвристически. Формальной называется обработка информации, которая производится исполнителем при строгом следовании выданной ему инструкции без учёта смысла обрабатываемой информации. Эвристическая обработка предполагает принятие решений о том, как производится обработка информации в зависимости от самой этой информации. Для конкретной ситуации далеко не всегда можно точно сказать, производится в данной ситуации алгоритмическая или эвристическая обработка информации. Это зависит, в частности, от тех знаний, которыми обладает тот, кто ведёт обработку информации.

7

Использование информации — обязательный элемент формирования целенаправленной деятельности. При использовании информации выявляются такие её свойства, как новизна, актуальность, достоверность, объективность, ценность, полнота и т. п.

Информация обладает новизной, если её смысловое содержание отличается от смыслового содержания ранее имевшейся информации.

Информация актуальна (иными словами, своевременна), если она оказывает влияние на формирование целенаправленной деятельности именно в данный момент времени.

Информация достоверна, если принимается, что она отражает реальное положение дел, в частности, не вступает в противоречие с уже имеющейся информацией, также признаваемой в качестве достоверной. Вовсе не исключается, что с поступлением новой информации данная информация уже перестанет быть достоверной.

Информация объективна, если она не зависит от свойств источника информации. Надо понимать, что абсолютно не зависеть от свойств источника информация не может, однако при тех или иных условиях можно считать, что такое влияние пренебрежимо мало.

Информация обладает ценностью (или, по-другому, полезностью), если она повышает вероятность достижения цели в целенаправленной деятельности той системы, которая использует эту информацию.

Информация полна, если её достаточно для достижения цели. Полная информация может быть избыточной, если для достижения цели достаточно только части данной информации.

Этими свойствами информация обладает в рамках конкретно протекающего информационного процесса.

^Ч

О Какую информацию называют символьной? Что такое видеоинформация?

Кроме символьной и видеоинформации, есть и другие виды информации. Информацию несёт запах; осязание доставляет нам тактильную информацию. Вкусовые рецепторы доставляют информацию о качестве пищи или готовности её к употреблению и т. д.

а) Приведите примеры использования человеком информации указанных видов.

б) Почему символьную и визуальную формы представления информации считают основными видами информации для человека?

О Назовите основные виды информационных процессов.

О Из перечисленных ниже процессов выделите информационные и укажите, к какому виду информационных процессов они относятся:

а) производство серной кислоты;

б) перевод из единиц измерения в системе СГСЕ в единицы си;

в) старт спортсменов в беге на дистанцию 100 м;

г) фотофиниш спортсменов в беге на дистанцию 100 м;

д) объявление победителей в беге на дистанцию 100 м;

е) награждение победителей в беге на дистанцию 100 м;

ж) измерение уровня кислотности раствора;

з) выпечка хлеба;

и) поиск грамматических ошибок в тексте;

к) уменьшение размеров тела при охлаждении;

л) составление меню обеда в школьной столовой;

м) выбор блюд из меню обеда в школьной столовой;

н) обед в школьной столовой.

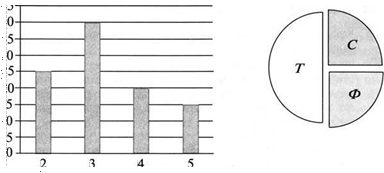
О В цехе трудятся рабочие трёх специальностей — токари (Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд не меньше второго и не больше пятого. На диаграмме, изображённой на рисунке 1.1, а, отражено количество рабочих с различными разрядами, а на диаграмме, изображённой на рисунке 1.1, б, — распределение рабочих по специальностям. Каждый рабочий имеет только одну специальность и один разряд по этой специальности. Кроме того, высказаны следующие утверждения, также относящиеся к этому цеху: а) Не могут все рабочие третьего разряда быть токарями.

б) Среди слесарей есть те, кто имеет разряд выше второго.

в) Все рабочие третьего разряда могут быть фрезеровщиками.

         а)                                                                б)

г) Все слесари могут быть пятого разряда.

д) Кто-то из токарей имеет разряд ниже четвёртого.

е) Среди работников третьего и четвёртого разрядов обязательно есть токари.

ж) Только фрезеровщики имеют четвёртый разряд.

з) Все рабочие третьего разряда могут оказаться фрезеровщиками.

Укажите, какие из этих утверждений не противоречат данным обеих диаграмм.

О В некотором классе для изучения изменения трудоспособности учащихся было проведено анкетирование. Один из школьников дал следующие ответы на вопросы анкеты:

а) Лучше всего работается в среду.

б) Самый непродуктивный день — суббота.

в) К концу недели продуктивность падает.

г) В течение недели не бывает больше двух дней с одинаковой продуктивностью.

д) В понедельник продуктивность такая же, как в пятницу.

е) В четверг работается хуже, чем во вторник, но лучше, чем в пятницу.

ж) Вторник — второй по продуктивности день.

Кроме того, в течение той же недели для того же школьника была составлена диаграмма изменения его трудоспособности, измеренной в условных единицах (рис. 1.2).

Укажите, какие из субъективных ощущений школьника совпадают с объективными показателями.

Тяжёлая атлетика — это прямое соревнование, когда каждый  атлет имеет три попытки в рывке, а затем три попытки в толчке. Самый тяжёлый вес поднятой штанги в каждом упражнении суммируется в общем зачёте. Если спортсмен потерпел неудачу во всех трёх попытках в рывке, он может продолжить соревнование в толчке, но уже не сможет занять какое-либо место по сумме двух упражнений.

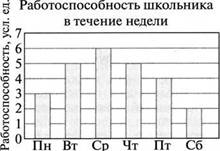
Рис. 1 2

Если два спортсмена заканчивают состязание с одинаковым итоговым результатом, высшее место присуждается спортсмену с меньшим весом. Если же вес спортсменов одинаков, преимущество отдаётся тому, кто первым поднял победный вес. Рассмотрите таблицу результатов соревнований по тяжёлой атлетике.

Ф.И.О.	Вес спортсмена	Взято в рывке	Рывок с попытки	Взято в толчке	Толчок с попытки
Арестов В. И.	77,1	147,5	2	200,0	2
Борисов Е. В.	79,1	147,5,	1	202,5	1
Воронкин Б. А.	78,2	147,5	2	200,0	1
Гончаров С. Т.	78,5			202,5	1
Климов К. С.	79,5	150,0	1	200,0	1
Лапин В. А.	77,1	147,5	2	200,0	1
Минин П. С.	78,5	150,0	з	200,0	2
Тарасов О. В.	78,5	147,5	1	202,5	2
Устинов К. Л.	77,6			202,5	2
Юдин А. С.	78,2	147,5	З	202,5	з
Якушев М. А.	77,3	150,0	1

а) Кто стал победителем по сумме двух упражнений?

б) Какое место по сумме двух упражнений занял П. С. Минин?

в) У кого лучший результат в толчке?

г) Кто выступил лучше по сумме двух упражнений: В. И. Арестов или В. А. Лапин?

д) Чей результат по сумме двух упражнений оказался худшим? Определите в каких случаях информация, которую намерен получить Петя, избыточна, а в каких недостаточна для того, чтобы сделать требуемый вывод (возможно также, что информации будет достаточно и она не избыточна).

а) Требуется определить, является ли данный четырёхугольник прямоугольником. петя собирается измерить все четыре угла этого четырёхугольника и убедиться, что каждый из них составляет 90⁰ .

б) Требуется определить, принимает ли данный квадратный трёхчлен только положительные значения при всех значениях независимой переменной. Петя намерен проверить отрицательность дискриминанта этого трёхчлена.

О В приведённых ниже примерах определите, полна ли информация для принятия требуемого решения. Если, на ваш взгляд, она не полна, то какую ещё информацию вы хотели бы иметь? а) Вы хотите подключиться к сети Интернет. Вы выяснили, какие провайдеры предоставляют такую услугу, сколько стоит подключение к сети и какова абонентская плата у каждого из провайдеров.

б) Вы собираетесь продолжить своё образование в вузе. У вас есть справочник для поступающих, где про каждый вуз сказано, по каким специальностям ведётся подготовка, каковы требования к поступающим, проводятся ли дополнительные вступительные испытания и в какие сроки они проходят, продолжительность обучения, формы обучения (очная, заочная, на платной или бесплатной основе и т. п.).

2 Кодирование символьной информации

Для передачи информации или её хранения в виде того или иного сообщения требуется определённый способ кодирования. Кодирование своей главной целью имеет сохранение информации и придание ей формы, обеспечивающей полноценную (т. е. без потерь и искажений) передачу информации от источника к получателю.

Знаковую систему, используемую для представления информации, называют языком. Языки бывают коммуникативные (языки межчеловеческого общения), формализованные (состоящие из терминов и обозначений, за которыми закреплён однозначный смысл) и формальные (определённые формальными синтаксическими правилами). По своему происхождению языки делятся на естественные и искусственные. К формальным искусственным языкам относятся все языки программирования. Примером коммуникативного искусственного языка является эсперанто.

Вся информация, циркулирующая в компьютере, закодирована в двухсимвольном алфавите. Для представления символьной информации в компьютере используются кодовые таблицы. Стандартной является кодовая таблица ASCII (American Standard Code for Information Interchange). В таблице П. 1, в Приложении, приведена основная часть этого кода, содержащая латинский алфавит, цифры и ряд вспомогательных символов. Расширения этой таблицы с символами национальных языков получили название кодовых страниц. Для русского языка это прежде всего кодовые страницы СР-866 и СР-1251 (последнюю называют ещё Windows-1251). В таблицах П.2 и П.З приведены эти страницы. В сети Интернет используется таблица КОИ-8 (Код Информационного Обмена 8-битовый). В Приложении она представлена таблицей П.4. Для экономии места мы не приводим в этих таблицах двоичные коды символов, а только указываем их десятичный порядковый номер.

О В таблице приведён код азбуки Морзе.

			ы

а) Закодируйте с помощью азбуки Морзе сообщение «ИНФОРМАТИКЕ ПРИНАДЛЕЖИТ БУДУЩЕЕ».

б) Какое сообщение передано с помощью азбуки Морзе?

О В сообщении, переданном с помощью азбуки Морзе, потеряно разделение на буквы:

Известно, что в передаче этого сообщения использовалось не более пяти различных символов: А, В, Д, Н, С. Попытайтесь восстановить сообщение.

О Пусть стрелка означает перемещение на одну клетку вверх, стрелка означает перемещение на одну клетку вниз, стрелка — перемещение на одну клетку влево, стрелка — перемещение на одну клетку вправо.

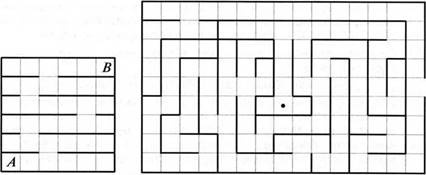
Рис. 2.1                          Рис. 2.2

а) Закодируйте последовательностью стрелок кратчайший маршрут из клетки А в клетку В на клетчатом поле с перегородками, изображённом на рисунке 2.1. (За один ход можно переместиться ровно на одну клетку, при этом запрещается проходить сквозь перегородки.)

б) Закодируйте последовательностью стрелок путь от входа лабиринта, изображённого на рисунке 2.2, до его центра (отмеченного точкой).

О Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трёх состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?

О Для пяти букв русского алфавита заданы их двоичные коды:

А—ОО1; к— 100; н— 10; 0— 101; т— 01.

Какое слово русского языка, состоящее из этих букв, закодировано двоичной строкой 100101100100110001?

о Для пяти букв латинского алфавита заданы их двоичные коды: А— 10; В — 01; С— 110; D — 101; Е— 010. Декодируйте сообщение 1001010111001, о котором известно, что каждая из пяти букв фигурирует в этом сообщении ровно один раз.

Представьте двоичным кодом в трёх различных кодировках текст «Время — вперёд!».

О Представьте десятичным кодом в трёх различных кодировках текст «Без труда не вынешь рыбку из пруда!».

О На листе бумаги было записано (по-русски) несколько терминов, относящихся к информатике. В каждом слове каждую букву заменили её порядковым номером в алфавите (вместо «а» написали 1, вместо «л» — 13 и т. д.). Получились следующие последовательности цифр: 11341618102014, 12161417303220618, 118231031241033. Восстановите закодированные слова. Символ «пробел» играет в тексте сообщения важную роль — ведь без него текстслипсябы,ичитатьегобылобыпростопротивно. Но роль этого символа не ограничивается обеспечением удобства чтения текста. Без него иногда просто невозможно однозначно разделить последовательность букв на осмысленные слова. Например, последовательность букв «поленоров» можно разбить пробелом на два осмысленных слова двумя способами — «поле норов» и «полено ров». Впрочем, допустимо ещё и разбиение двумя пробелами в три слова — «поле но ров».

а) Каким образом текст «Поднимитеперьятакже» можно разбить пробелами на слова так, чтобы получалась осмысленная фраза? Приведите как можно больше вариантов.

б) Придумайте ещё какие-нибудь последовательности букв, допускающих неоднозначное разбиение пробелом на группы слов русского языка.

З

•              Кодирование числовой информации

Знаки, посредством которых кодируется числовая информация, называются цифрами. Способ представления числовой информации с помощью цифр называется системой счисления. Различают позиционные и непозиционные системы счисления. В позиционной системе значение цифры зависит от того, где эта цифра расположена в записи числа. Это место называют разрядом; разряды нумеруются слева направо. В непозиционных системах значение цифры не связано с занимаемым ею местом.

3.1. Позиционные системы счисления с произвольным основанием

Среди позиционных систем особую роль играют системы, в которых каждый следующий разряд в Ь раз больше предыдущего (Ь — фржсированное для данной системы число, большее 1). В этом случае Ь называют основанием системы, а саму систему счисления называют Ь-ичной. Для записи любого натурального числа в Ь-ичной системе требуется Ь цифр. Обычно используются цифры от О до Ь — 1 ¹ .

Другие возможные варианты цифр рассматриваются в п. 4.3.

Запись а102 ... ап _ является представлением числа с в позиционной системе счисления с основанием Ь, если

причём каждый коэффициент ai неотрицателен и меньше Ь. Из этого равенства видно, что последняя цифра ап представляет собой остаток при делении числа с на Ь. А частное от такого деления используется для нахождения предпоследней цифры ап_ — она получается как остаток при делении этого частного снова на Ь. И т. д.

Алгоритм обратного перевода заключается в следующем. В одной строке записывается число, которое нужно перевести, а строкой ниже будет вычисляться запись числа в нужной системе счисления. Для этого первая цифра переписывается без изменения, а под каждой следующей цифрой записывается число, полученное сложением этой цифры с произведением слева стоящего числа на основание системы счисления. Этот алгоритм называется схемой Горнера.

Позиционный принцип распространяется и на дробные числа: запись а1а2  ... а является представлением дробного числа с в системе счисления с основанием Ь, если

где по-прежнему каждый коэффициент ai неотрицателен и меньше Ь. Указанные выше алгоритмы перевода соответствующим образом модифицируются.

Главное удобство позиционной нумерации состоит в том, что действия над числами в такой системе счисления выполняются поразрядно. Всё, что требуется знать для выполнения действий над многозначными числами, — это таблицы сложения и умножения для однозначных чисел.

Если число записано не в десятичной системе счисления, то основание системы будем записывать в виде нижнего индекса справа от числа, например 136, 35711. В случае, когда основание системы ясно из контекста, мы не будем, как и для десятичной системы, писать этот индекс.

О Будет ли позиционной система счисления, в которой для записи чисел используется ровно одна цифра?

О Запишите наименьшее и наибольшее п-разрядные числа в системе счисления с основанием Ь при:

Каждую пару полученных чисел переведите в десятичную систему счисления.

О Сравните числа:

а) 12349 и 7659; б) 3454311 и 4363411;

в) 77777777777777777725 и 777777777777777777725;

г) 535353535353535353535353 и 45353535353535353535353.

О К чему приводит умножение на 7 числа, записанного в шестеричной системе счисления? А умножение на 49?

а) Составьте таблицы сложения и умножения в шестеричной системе счисления.

б) Используя результат пункта а, вычислите 546 + 456 и 546 . 456.

О Переведите числа 634 и 5321 в системы счисления с основанием: а) 5; б) 7; в) 9.

Переведите в десятичную систему счисления числа: а) 7549; б) 214511; в) 32 47512; г) 21467; д) 24 5849.

О Переведите в десятичную систему счисления дробные числа:

а) 75,69; б) 23,8811; в) 345,9612; г) 65,237; д) 57,0639.

Ответ запишите обыкновенными дробями.

О Переведите в пятеричную систему счисления дробные числа:

а) 73,2; б) 32,87; в) 30,84; г) 45,23; д) 84,268.

Результат, если необходимо, округлите до шестого разряда после запятой.

Определите, может ли в какой-либо системе счисления быть верным равенство:

а) 7+8= 13; б) 7+8=20; в) 7+8=23.

О для каждого из следующих равенств определите основание системы счисления, в которой оно справедливо:

а) Укажите все основания системы счисления, после перевода в которую числа 4710 получается число, оканчивающееся на цифру 2.

б) Укажите все основания системы счисления, для которой после перевода в неё десятичного числа 4110 получается число, оканчивающееся на цифру 6.

В системе счисления с некоторым основанием десятичное число 12 записывается как 110. Укажите это основание.

У отца, увлекающегося математикой, спросили о его детях. он ответил так: «У меня 11 детей. Все они учатся в школе. Младшему из них 100 лет, а старший заканчивает 101 -й класс». В какой системе счисления названы все числа в этом рассказе? Сколько детей у этого отца?

Чему равно х, если выполнено равенство:

          а) 15х+272х= 136х; 6) 103х +          1289

для двух позиционных систем счисления с основаниями х и у выполняется равенство 486х = 902 . Какое наименьшее значение может иметь х?

 а) Для позиционных систем счисления с основаниями х, у и ху выполняется равенство 35х + 23 = 16ху. Найдите х и у.

б) Найдите все такие пары натуральных чисел х и у, чтобы в системах счисления с основаниями х, у и ху выполнялось равенство 23х + 34у = 19ху

а) В системе счисления с основанием х число, записываемое как 54, является квадратом целого числа. Найдите наименьшее возможное значение х.

б) Выполните то же задание для числа, записываемого как 72.

в)* Существует ли такая позиционная система счисления, в которой число, записанное как 32, является квадратом целого числа?

г)* Ответьте на тот же вопрос для чисел, записанных как 42 И 43.

Натуральное число в десятичной системе счисления оканчивается на цифру 7, а при переводе его в девятеричную и двенадцатеричную системы счисления получаются числа, оканчивающиеся на цифру 5. Какое наименьшее число обладает таким свойством?

Наиболее известная из непозиционных систем счисления — римская нумерация. В ней семь цифр: 1, V, Х, С, D, L, М. Они означают соответственно 1, 5, 10, 50, 100, 500, 1000. Если меньшая цифра стоит справа, то значение прибавляется к значению предыдущей, а если слева, то вычитается.

а) Число MDD<l записали в десятичной системе, затем поменяли местами две средние цифры. Запишите получившееся число снова римскими цифрами.

б) Выполните такое же задание для числа MLDCll.

3.2. Системы счисления, используемые в программировании

В компьютере вся информация представляется в двоичном коде. Поэтому для кодирования числовой информации применяется двоичная система счисления. Чтобы уменьшить длину записи, в программировании используются восьмеричная и шестнадцатеричная системы счисления. Десятичные, двоичные, восьмеричные и шестнадцатеричные коды первых шестнадцати натуральных чисел представлены в таблице.

2— Гейн. Задачник-практикум, 10—11

Десятичная система счисления	Двоичная система счисления	Восьмеричная система счисления	Шестнадцатеричная система счисления
1 2 з 4 5 6 7 8 9 10 11 12 13 14 15 16	1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 10000	1 2 З 4 5 6 7 10 11 12 13 14 15 16 17 20	1 2 з 4 5 6 7 8 9 в с 10

Для систем с основанием Ь = 2 ^s существует простой алгоритм перевода из двоичной системы в систему с основанием Ь. Для этого запись числа в двоичной системе разбивают на блоки по s цифр, начиная от разряда единиц, и каждую такую группу заменяют цифрой соответствующей системы счисления (при Ь = 8 такой блок называют триадой, при Ь = 16 его называют тетрадой). Обратный перевод осуществляется расписыванием каждой цифры её представлением в двоичной системе счисления.

а) Переведите из десятичной в двоичную, восьмеричную и шестнадцатеричную системы числа: 27, 72, 123, 987, 10101. б) Пользуясь инженерным калькулятором, переведите из десятичной в двоичную, восьмеричную и шестнадцатеричную системы числа: 2347, 32 568, 777 777.

Переведите из двоичной в десятичную систему числа: 1011, 11001, 11011, 10101101.

Переведите из восьмеричной в десятичную систему числа: 25, 47, 173, 721, 2345, 7777.

О а) Переведите из шестнадцатеричной в десятичную систему счисления числа: 52, F4, А7В, BCD.

б) Пользуясь инженерным калькулятором, переведите из шестнадцатеричной в десятичную систему счисления числа: ED1A, FOFO.

Сколько существует натуральных чисел, меньших 1000, содержащих в своей записи ровно три единицы после перевода их в двоичную систему счисления?

О Переведите из двоичной в восьмеричную и шестнадцатеричную системы счисления следующие числа:

а) 1011; 11001; 11011; 10101101;

           б)         10,01; 1010,1; 11,1011; 1011,1101.

Переведите из шестнадцатеричной в двоичную систему счисления следующие числа:

а) 31; 6F; 2А9; АСЕ; D1AE; FFFE;

              б)              3,1; 5,F; 2А,9; А,СЕ; D1,AE; F,FFF.

О Переведите из шестнадцатеричной в восьмеричную систему счисления следующие числа:

а) 31; 6F; 2А9; АСЕ; D1AE; FFFF;

              б)              3,1; 5,F; 2А,9; А,СЕ; D1,AE; F,FFF.

О Переведите из восьмеричной в двоичную систему счисления следующие числа:

а) 31,47; 216; 654; 5432; 7070.

           б)          3,1; 0,47; 2,16; 65,4; 54,32; 7,077.

Переведите из восьмеричной в шестнадцатеричную систему счисления следующие числа:

а) 31,47; 216; 654; 5432; 7070;

           б)          3,1; 0,47; 2,16, 65,4, 54,32; 7,077.

О а) Натуральное число А, записанное в шестнадцатеричной системе счисления, четырёхзначно, а будучи записанным в восьмеричной системе счисления становится пятизначным. Какое наименьшее значение может иметь число А? А наибольшее? Ответ дайте в десятичной системе счисления.

б) Натуральное число А, записанное в восьмеричной системе счисления, семизначно, а будучи записанным в шестнадцатеричной системе счисления становится шестизначным. Какое наименьшее значение может иметь число А? А наибольшее? Ответ дайте в десятичной системе счисления. Сравните между собой числа, записанные в двоичной системе счисления:

а) 10101 и 101010; б) 1101 и 1001; в) 111001 и 110111.

для пары чисел из пункта в определите, на сколько одно число больше другого.

Расположите числа в порядке возрастания:

а) 2А,З16; 41,2510; 51,18; 101010,0012;

б) 1C,616; 28,7510; 34,58; 11100,1112;

в) 13,Е16; 19,710; 23,58; 10011,1112.

Среди всех чисел, заключённых между числами 515 и 580, найдите те, которые после перевода в двоичную систему содержат в своей записи наибольшее количество единиц.

Составьте таблицы сложения и умножения в системе счисления с основанием: а) 2; б) 8; в) 16.

Используя результат задания 15а, найдите в двоичной системе счисления:

а) суммы 1011 + 1101, 101,01 + 100,01 и 101,01 + 110,11;

б) разности 110 101 - 101 111 и 100 000- 11,1;

в) произведения 111 • 101 и 101,01 • 101,11;

г) целочисленное частное и остаток при делении 101 101 на 100 и 100 001 на 101.

Используя результат задания 156, найдите в восьмеричной системе счисления:

а) суммы 2222 + 6666 и 671,76 + 370,3;

б) разности 101 - 110 111 и 100 000- 11,1;

в) произведения 567 • 321 и 570,25 • 543,04;

г) целочисленное частное и остаток при делении 707 707 на 100 и 100 000 на 707.

Используя результат задания 16в, найдите в шестнадцатеричной системе счисления:

а) суммы 8888 + 5555 и ABCD,F+30 70,3;

б) разности 111 101 - 101 111 и 100 000- 1,11;

в) произведения 7А5 . 1B3 и C4D,5 • F4A,6B;

г) целочисленное частное и остаток при делении FFFFFF на 100 и 100 000 на FFF.

а) Найдите значение выражения 1 1016 . 102 - 1008 : 102. ответ дайте в системе счисления с основанием 4.

Решите уравнение 11012+ 102 х = 1010102. Ответ дайте в системе счисления с основанием 8.

а) Используя кодовую таблицу СР- 1251 (см. Приложение, табл. П.З), закодируйте фразу «Знание — сила!» в двухсимвольном алфавите (О и 1) и полученный двоичный код запишите шестнадцатеричными цифрами.

б) Выполните такое же задание для фразы «Никто не забыт, ничто не забыто!», используя кодовую таблицу КОИ-8 (см. Приложение, табл. ПА).

в) Придумайте какую-нибудь фразу, закодируйте её в двухсимвольном алфавите с помощью кодовой таблицы СР-866 (см. Приложение, табл. П.2) и полученный двоичный код запишите восьмеричными цифрами. Передайте полученное вы-

ражение соседу по парте и предложите восстановить исходную фразу. Проверьте, правильно ли он выполнил задание. Замените звёздочки цифрами так, чтобы получились верные записи примеров в двоичной системе счисления:

в)

3.3. Уравновешенные и другие системы счисления

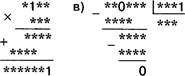
В позиционной системе счисления с нечётным основанием Ь в качестве цифр могут использоваться целые числа

в диапазоне от —       до           Такая система счисления на-

2            2 зывается уравновешенной. В уравновешенных системах счисления в записи отрицательных цифр вместо знака «—» обычно пишут черту над цифрой. Алгоритмы перевода из десятичной системы счисления в уравновешенную систему с основанием Ь (последовательное деление с остатком) и обратно (схема Горнера) остаются теми же — надо только при делении выделять остаток, заключённый между

 и

      2           2

В нашей стране в 70-х гг. был создан компьютер «Сетунь», выполнявший вычисления в троичной уравновешенной системе счисления.

О Напишите цифры, которые используются в уравновешенной системе счисления с основанием: а) З; б) 5; в) 11. Запишите З; 5; 121; 534; —2; —16; —121 в уравновешенной системе счисления:

а) с основанием З; б) с основанием 5; в) с основанием 11.

О а) Переведите в обычную десятичную систему счисления числа, записанные в уравновешенной троичной системе счисления: 10T1; 1T1T01; Т1Т; 1 ТОТ 1; ТТ ТТ.

б) Переведите в обычную десятичную систему счисления числа, записанные в уравновешенной системе счисления с основанием 5: 102Т 1; 1T02; тто21; 2T1T.

в) Переведите в обычную десятичную систему счисления числа, записанные в уравновешенной системе счисления с основанием 11: 153T1•, 5T22•, топа; 2T6T4.

О а) Сформулируйте правило сравнения двух целых чисел, записанных в одной и той же уравновешенной системе счисления.

б) Сформулируйте правило, по которому осуществляется переход от числа, записанного в данной уравновешенной системе счисления, к противоположному числу.

О а) Составьте таблицы сложения и умножения однозначных чисел в троичной уравновешенной системе счисления.

б) Составьте таблицы сложения и умножения однозначных чисел в пятеричной уравновешенной системе счисления.

О а) Сформулируйте правило сложения двух целых чисел, записанных в одной и той же уравновешенной системе счисления. б) Сформулируйте правило умножения двух целых чисел, записанных в одной и той же уравновешенной системе счисления.

О Выполните действия в троичной уравновешенной системе счисления:

                                          б) 110101 +T010T;

           в) Т11Т11 Т + 1Т1Т1Т1Т;              г) 1010T11 +ToT01TT;

            д) 10T1T01 -T0110TT•,                 T10T1;

            ж) 1T01T1 .T10T01;                     з)*1Т11 Т . 111.

О Выполните действия в пятеричной уравновешенной системе счисления:

            а) 21212+ 121212;                       6) Т20121 +22122;

              в) 22222 + 10201;                          г) 2T10T2 +2212T1;

                     д) 2ToTT01 -тоаотт1;                            е) 2T02 • Т2Т1.

 Кодирование видеоинформации

Цветное изображение на экране компьютера образуется смешением трёх основных цветов: красного, синего и зелёного. Изменение интенсивности того или иного цвета и создаёт нужный оттенок, воспринимаемый человеческим глазом как единое целое. В таблице приведено кодирование цветов, если для каждого цвета есть только две возможности — светиться с определённой интенсивностью (кодируется 1) либо не светиться вообще (кодируется О). Указанное кодирование цвета называется RGB-k0дировкой (от английского названия цветов — Red, Green, Blue).

Красный	Синий	Зелёный	Цвет
		о	Чёрный
		1	Зелёный
	1	О	Синий
1		о	Красный
	1	1	Бирюзовый
1		1	Жёлтый
1	1	о	Малиновый
1	1	1	Белый

Для кодирования графической информации на экране его делят на множество рядов одинаковых квадратиков. Каждый такой квадратик называется пиксель (от английского PICture'S ELement — элемент картинки). Число строк на экране и количество пикселей в строке называют разрешением заданного графического режима.

В современных компьютерах используется 16-битное (режим Hi-Color) и 24-битное (режим True-Color) кодирование. В первом случае оказывается возможным закодировать 2 ¹⁶ = 65 536 цветов, во втором — 2 ²⁴ = 16 777 216 цветов. В режиме True-Color на кодирование градаций яркости каждого из основных цветов отводится 1 байт: код 00000000 показывает, что данного цвета нет вообще, а код

сти) кодируемого цвета. В случае 16-битного кодирования ситуация иная: на кодирование яркости красного и синего цветов отводится по 5 битов, а на кодирование зелёного цвета — оставшиеся 6 бит.

О Что является пикселем в случае цветного монитора и почему он так называется?

для хранения растрового изображения размером 128 х 128 пикселей отвели 4 Кб памяти. Каково максимально возможное  число цветов в палитре изображения?

О Растровый графический файл содержит цветное изображение с палитрой из 256 цветов размером 10 х 10 пикселей. Каков информационный объём этого файла?

О а) Один из самых первых графических режимов, называвшийся сокращённо CGA (от Crayon Graphics Adaptor — графический адаптер «как цветной карандаш»), предусматривал 320 >< 200 пикселей на экране. Каждый из пикселей мог гореть одним из восьми цветов — именно тем, КОТОРЫЙ указан в таблице. Сколько бит требовалось, чтобы закодировать изображение в этом режиме?

б) Выполните то же задание для режима VGA (Video Graphics Adaptor) и экрана 640 х 480 пикселей. При этом каждый элемент триады допускает не две, а 64 градации яркости. В процессе преобразования растрового графического файла его объём уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования было получено растровое изображение того же разрешения в 256-цветной палитре?

О а) Набору яркостей (1/2; 0; 1/2) соответствует фиолетовый цвет. Какой цвет, по вашему мнению, соответствует набору (1/4; О; 1/4)? А набору (3/4; О; 3/4)?

б) Каким набором яркостей характеризуется бирюзовый цвет? Пусть используется режим True-Color. Укажите цвет, который задаётся кодом:

6) 100000001000000010000000;

О При кодировании цвета соответствующая битовая последовательность нередко записывается в виде шестнадцатеричного числа. Укажите цвет, который задаётся кодом:

           а) FFOOFF; б) СССССС; в) 009900;         FF9933.

О При кодировании цвета в режиме True-Color битовая последовательность, соответствующая коду каждого основного цвета, рассматривается как натуральное число в двоичной системе и переводится в десятичную систему счисления. В коде всей триады цветов эти десятичные числа отделяются друг от друга точкой. Например, зелёный цвет задаётся как 0.255.0. Укажите цвет, который задаётся десятичным кодом:

              а) 0.255.255; б) 102.102.102; в) 204.0.204;              204.51.255.

Пусть используется режим Hi-Color. Укажите цвет, который задаётся кодом:

О При печати цветного изображения на бумаге используется иная кодировка цвета. Связано это с тем, что изображение создаётся лучами, отражёнными от белого листа бумаги, а типографская краска представляет собой светофильтр, поглощающий ту или иную составляющую белого цвета (который, как известно из физики, является смесью всех цветов спектра).

а) Возьмите лупу и рассмотрите какую-либо цветную иллюстрацию в книге. Из каких цветов, кроме чёрного, составлено изображение?

6)* Выполнив задание а, вы обнаружили, что, кроме чёрной, при печати используется краска трёх цветов: малинового, бирюзового и жёлтого. Бирюзовый цвет на бумаге поглощает красную составляющую. Синий цвет поглощается жёлтым, а зелёный — малиновым. Чёрный цвет получается, если нанести на бумагу все три поглощающих цвета. Сказанное выше занесено в три строки следующей таблицы.

Бирюзовый (нет красного)	Жёлтый (нет синего)	Малиновый (нет зелёного)	Цвет
		о
		1	Малиновый
	1		Жёлтый
1			Бирюзовый
	1	1
1		1
1	1
1	1	1

Заполните остальные строки таблицы. (Со в е т: догадайтесь, как для этого использовать таблицу, приведённую на с. 23.)

в)* Кодировка, которая рассмотрена в пункте б, называется СМУ-кодировкой (по первым буквам английского названия основных цветов — Суап, Magenta, Yellow). Пусть интенсивность каждого цвета в  принимает значения от О до 1. Иными словами, каждый цвет кодируется тройкой чисел, в которой вначале идёт доля красного цвета, затем зелёного и, наконец, синего. Бирюзовый цвет, таким образом, будет иметь  (О, 1, 1). Аналогично в СМУ-кодировке каждый цвет задаётся тройкой чисел, показывающей долю бирюзового, жёлтого и малинового цветов.

Напишите формулы перехода из  в СМУ-кодировку.

Коды, обнаруживающие и исправляющие ошибки

В ходе передачи информации внешние воздействия могут вносить изменения в передаваемый код. Чтобы устранить воздействие внешних помех, код делают избыточным, т. е. передаваемая информация кодируется не минимально необходимым количеством бит, а с использованием дополнительных двоичных символов. Это позволяет автоматизировать поиск и исправление ошибок.

Базовым инструментом в автоматическом поиске и исправлении ошибок является понятие расстояния Хэмминга. Расстоянием Хэмминга между двумя битовыми последовательностями одинаковой длины называют количество позиций, в которых эти две последовательности различаются. Множество всех битовых последовательностей, используемых для кодирования символов заданного алфавита, называется кодом. Кодовым расстоянием называется минимальное из расстояний между любыми двумя последовательностями, принадлежащим данному коду. Пусть d — кодовое расстояние. Если при передаче кода символа количество искажённых бит оказалось не

больше чем , то имеется ровно одна кодовая последо2 вательность, ближайшая к той последовательности, которая получена приёмником сообщения. В этом случае именно эта последовательность принимается за исходно переданную.

О Чему равно расстояние Хэмминга между последовательностями:

в) 101101010101 и 001010100101?

О Рассматривается множество всех пятисимвольных слов над алфавитом {0, 1}.

а) Перечислите все слова, находящиеся на расстоянии 1 от слова 11101. б) Перечислите все слова, находящиеся на расстоянии 2 от слова 01011.

в) Сколько существует слов, находящихся на расстоянии З от

О для кодирования 15 букв русского алфавита и пробела использовался код, представленный в таблице.

Буква	код	Буква	Код
Пробел	0000000	з	1000011
	1001100	и
	1110000	й	0010110
в	1100110	к	0011001
	1011010	л	0100101
д	1010101	м	0101010
		н	0110011
ж	1101001	о

а) Найдите кодовое расстояние. Сколько ошибок гарантированно исправляет этот код?

б) Получено сообщение

Попытайтесь его декодировать, исправив, если необходимо, ошибки.

в) Выполните такое же задание для следующего сообщения:

110110110100010001101000100010001 1 1 1101 1 10111 1011011 1

г) Придумайте небольшое сообщение (10—12 символов), составленное из букв, фигурирующих в таблице из задания З, закодируйте его, внесите в кодировку некоторых символов по одной ошибке и предложите соседу по парте декодировать сообщение. Проверьте, как он выполнил эту работу.

О* Попытайтесь обосновать высказанное выше утверждение, что для кода с кодовым расстоянием d любая последовательность, которая не более чем в (d — 1 )/2 местах отличается от некоторой кодовой последовательности, есть ровно одна ближайшая к ней кодовая последовательность.

б Измерение количества информации

Понимание, что является мерой для количества информации, зависит от трактовки самого понятия информации (см. преамбулу данного раздела). Каждый из получающихся в этом случае подходов к измерению количества инфор-

мации представлен в пунктах этого параграфа. Тем не менее независимо от подхода единицей измерения информации является 1 бит (от английского BInary digiT двоичная цифра). Обычно используются более крупные единицы измерения информации — 1 байт, 1 килобайт (Кб), 1 мегабайт (Мб), 1 гигабайт (Гб) и т. д. Соотношение между этими единицам таково:

1 байт = 8 бит

— 1024 байт

1 Мб = 1024 Кб

1 Гб = 1024 Мб

О Каков коэффициент пересчёта байтов в килобайты; килобайтов в мегабайты? А коэффициент пересчёта битов в байты? Сколько байт в одном мегабайте? А бит?

6.1. Информационный объём сообщения

Любая информация, представленная в виде сообщения, может быть закодирована в двухсимвольном алфавите, Количество символов в такой кодировке называют информационным объёмом сообщения.

Количество информации, закодированной одним символом двоичного алфавита, принимают за 1 бит.

Для кодирования символьной информации в компьютере применяется обычно 8-битный код ASCII или 16-битный код UNICODE.

Если сообщение закодировано в  алфавите, то информационный объём одного символа принимают равным log2 N. Этот коэффициент используется при подсчёте количества информации, записанной не в двухсимвольном алфавите.

О а) Информационный объём сообщения равен 40 бит. Выразите объём того же сообщения в байтах.

б) Информационный объём сообщения равен 23 Кб. Выразите объём того же сообщения в байтах и битах.

а) В сообщении «Компьютер — основное средство информационных технологий.» каждый символ кодируется в системе UNlCODE. Подсчитайте информационный объём этого сообщения в байтах.

б) В сообщении «С. А. Лебедев — создатель первой отечественной ЭВМ.» все символы кодируются в системе ASCll. Подсчитайте информационный объём этого сообщения в байтах.

О Подсчитайте, каков информационный объём этой страницы задачника, округлив полученный результат до целого числа килобайт (колонтитул и номер страницы не учитываются).

О а) Сколько символов можно закодировать, используя ASCll? б) Сколько символов можно закодировать, используя UNlCODE? а) Автоматическое устройство осуществило перекодировку информационного сообщения длиной в 35 символов, первоначально записанного латинскими буквами в коде UNlCODE, в кодировку ASClt. На сколько изменился информационный объём сообщения?

б) Автоматическое устройство осуществило перекодировку информационного сообщения длиной в 35 символов, первоначально записанного русскими буквами в кодировке СР- 1251, в UNlCODE. На сколько изменился информационный объём сообщения?

О Для передачи секретного сообщения используется код, состоящий из десятичных цифр. При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объём сообщения длиной в 200 символов.

О В велокроссе участвуют 106 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объём сообщения, записанного устройством, после того как промежуточный финиш прошли 95 велосипедистов?

О В России каждый автомобильный номер состоит из трёх заглавных букв и трёх цифр (всего в различных номерах задействовано 12 букв русского алфавита, совпадающих по начертанию с буквами латинского алфавита, и все 10 цифр). При этом на первом и двух последних местах стоят буквы, на трёх оставшихся местах стоят цифры. Каждый такой номер записывается минимально возможным и одинаковым целым количеством байт (при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, необходимой для записи 700 номеров.

О а) «Сколькибитное» кодирование вы бы предложили для языка племени «Мумбо-Юмбо», в алфавите которого 32 буквы и все заглавные, а цифр и знаков препинания и вовсе нет? б) Если в пункте а ваш ответ — 5, то найдите ошибку. Без какого символа нельзя обойтись?

зо

ДНК человека (его генетический код) можно представить как слово в четырёхбуквенном алфавите — каждая буква обозначает некоторое звено цепи ДНК. Каков информационный объём ДНК, содержащей примерно 1,5 • 1023 звеньев?

Сообщение, присланное от инопланетян, оказалось записанным с помощью всех символов их алфавита. Вот это сообщение:

Все символы алфавита кодируются одним и тем же минимально необходимым числом бит. Сколько бит информации в этом сообщении?

В марсианском алфавите 15 букв, в венерианском — 255 букв. Кроме того, в каждом языке есть символ «пробел», разделяющий слова. При передаче сообщений применяется двоичное кодирование, в котором каждый символ кодируется одинаковым числом бит. Жители этих планет обменялись сообщениями, содержащими одинаковое количество символов. Каждый при этом писал на своём языке, поэтому информационный объём сообщений оказался разным.

У какого сообщения информационный объём оказался больше и во сколько раз?

Рассмотрите свои ответы к заданиям З из 2. Сколько бит содержит сообщение о маршруте из клетки А в клетку В, о котором шла речь в задании ба?

Сколько информации содержит следующая картинка, напечатанная компьютером?

Представьте себе, что из туманности Андромеды (одной из ближайших к нам галактик) пришло сообщение в виде последовательности радиосигналов двух видов (один из них мы обозначили нулём, а другой — единицей):

1 1 ooooooooooooooooooooooooooooooooo 1 100001 10000000000

000

а) Сколько бит информации содержит это сообщение?

б) Многие учёные считают, что жители высокоразвитых цивилизаций обладают органами чувств, аналогичными нашему зрению. Используя это предположение в качестве предварительной информации о цивилизации, попытайтесь расшифровать сообщение. (Совет: разложите количество бит информации на простые множители.)

В системе связи скорость передачи — 200 символов в минуту. В течение 5 мин было передано сообщение объёмом 375 байт. Сколько символов в алфавите?

Монитор работает в режиме с разрешением 1024 х 768 при глубине разрешения 32 бит и частоте обновления экрана 75 Гц. Какую минимальную пропускную способность должен поддерживать видеоадаптер, обеспечивающий работу монитора?

В системе связи скорость передачи составляет 128 ООО бит/с. На передачу файла с несжатой монофонической музыкой потребовалось 2 минуты и 45 секунд. Укажите количество уровней квантования при оцифровке этой музыки, если известно, что её продолжительность составила 1 минуту и оцифровка производилась с частотой дискретизации 22 ООО Гц.

для хранения данных на дискете 3,5” выделяется 2847 секторов, объёмом 512 байт каждый. Какова длительность звукового файла, который уместится на такой дискете при высоком качестве звука: стерео, 16 бит, 48 ООО измерений в секунду? (Совет: имейте в виду, что каждый раз должны быть записаны данные всех 48 ООО измерений.)

два текста содержат одинаковое количество символов, хотя и записаны в двух разных алфавитах. Количество символов в каждом алфавите не превышает 20. Вася заметил, что, хотя количество символов в первом алфавите в З раза больше, чем во втором, информационный объём первого текста всего лишь в 2 раза больше, чем второго. После этого Вася решил подсчитать, насколько в первом алфавите символов больше, чем во втором. Какое максимальное и какое минимальное число могло у него получиться, если известно, что все символы, принадлежащие одному алфавиту, кодируются одним и тем же минимальным целым числом битов, но, возможно, своим для каждого алфавита?

6.2. Экономное кодирование.

Алгоритмы сжатия информации

Использование одного и того же количества бит для кодирования всех символов алфавита весьма расточительно, ведь некоторые символы употребляются в сообщениях достаточно редко, а другие значительно чаще. Чтобы уменьшить информационный объём передаваемого сообщения, выгодно часто используемые символы кодировать меньшим количеством бит. Но чтобы такой неравномерный код позволял однозначно декодировать переданное сообщение, нужно, чтобы он обладал определёнными свойствами. Одним из условий, обеспечивающих однозначное декодирование, является префиксность кода: код называется префиксным, если код любого символа алфавита не является начальным фрагментом кода какого-либо другого символа. Многие алгоритмы сжатия информационного объёма сообщения построены на том, что более часто встречающиеся символы или комбинации символов кодируются более короткими битовыми последовательностями. Коэффициентом сжатия называется отношение исходного информационного объёма сообщения к информационному. объёму того же сообщения после того, как к нему применено сжатие.

Для каждого двоичного кода может быть построено двоичное дерево ^[1] , каждое ребро которого помечено одним из двух кодирующих символов. Последовательность символов от корня к любой вершине даёт слово, записанное в двухсимвольном алфавите. Код является префиксным в том, и только в том случае, когда все кодовые слова заканчиваются на листьях кодового дерева.

Алгоритмы сжатия бывают двух типов — без потери информации (обратимые алгоритмы) и с потерей информации. Алгоритмы первого типа используются, как правило, для сжатия символьной информации, алгоритмы второго типа — для сжатия видео- и аудиоинформации. К обратимым алгоритмам сжатия информации относится алгоритм Хаффмана. Он состоит в следующем:

1-й шаг — для каждого символа определяется количество его вхождений в сообщение;

2-й шаг — строится бинарное дерево, концевыми вершинами которого являются символы сообщения и каждой из них приписано количество вхождений этого символа, при построении новой вершины среди вершин, в которые ещё не входят рёбра, выбираются две вершины с наименьшими значениями; новая вершина соединяется рёбрами

с выбранными двумя вершинами, и ей приписывается число, равное сумме чисел на концах построенных рёбер;

3-й шаг — рёбра дерева размечаются символами О и 1, начиная от корня;

4-й шаг — каждому символу исходного сообщения сопоставляется кодовое слово, прочитанное на маршруте от корня к концевой вершине, соответствующей этому символу.

О Какой код называется префиксным?

О* Объясните, почему сообщение, записанное в префиксном коде, допускает однозначное декодирование. Опишите алгоритм декодирования для префиксного кода.

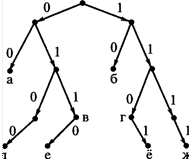О а) На рисунке 6.1 изображено двоичное дерево некоторого кода. Для каждой буквы запишите соответствующее ей кодовое слово. Является ли этот код префиксным?

б) «Перестройте» (т. е. не увеличивая количества вершин) это дерево так, чтобы для тех же 8 букв получился префиксный код.

О а) дан набор кодовых слов: 00, 10, 010, 101, 110, 1001, 1011, для этого кода соответствующее ему дерево. Является ли этот код префиксным?

б) Выполните такое же зада- Рис. 6.1 ние для кода 00, 01, 10, 011,

в) Выполните такое же задание для кода 00, 10, 010, 110, 0110, 0111,

для кодирования 7 букв русского алфавита и пробела использовался код, представленный в таблице:

Буква	Пробел		Б	в		д
код	01	111	001	1100	0000	10	0001	1101

а) Проверьте, что этот код префиксный.

б) Закодируйте сообщение «ГДЕ ЖЕ ЕДА».

З— Гейн. Задачник-практикум, 10—11

в) Декодируйте сообщение

О Для кодирования цифр предложено пять кодов: А, В, С, D и Е (см. таблицу).

		в	с	D	Е
о	1110	0010	1101	0011	0010
1	1010	101	1011	1101	101
2	111	0011	1010	011	0011
з	000	0000	0100	1100	0001
4	0010	011	111	1110	0101
5	100	11	001	000	1000
6	0011	0100	000	0010	0100
7	1101	100	100	10	11
8	1011	0001	010	010	100
9	01	0101	011		011

а) для каждого из этих кодов постройте кодовое дерево.

б) Укажите, какие из предложенных кодов являются префиксными.

в) Закодируйте каждым из найденных вами префиксных кодов следующие числа: 213; 1000; 8642.

г) После кодирования некоторого числа одним из найденных вами префиксных кодов получилась последовательность 100100110010000. Определите, каким кодом осуществлено кодирование, и восстановите исходное число.

д) Выполните такое же задание, как в пункте г, для последовательности 01101000101110.

е) Выберите какое-нибудь не более чем четырёхзначное число и закодируйте его одним из префиксных кодов, предложенных в таблице. Передайте получившийся код соседу по парте для декодирования. Проверьте, правильно ли он провёл декодирование (для этого пусть он укажет код, которым пользовался).

а) Постройте код Хаффмана для фразы «НА ДВОРЕ ТРАВА, НА ТРАВЕ ДРОВА».

б) Определите коэффициент сжатия для данной фразы, считая, что исходно каждый символ кодировался в ASCll.

О а) Постройте код Хаффмана для Фразы «КАК БЕЗДНА ЗВЁЗД БЕЗ ДНА НАД НАМИ НЕБО».

б) Определите     коэффициент сжатия для данной фразы, считая, что исходно каждый символ кодировался в UNlCODE.

О При кодировании графической информации довольно много идущих подряд пикселей имеют, как правило, один и тот же цвет и потому кодируются одним и тем же набором бит. Естественной идеей уменьшения информационного объёма является Рис. 6.2 простое указание, сколько пикселей, идущих друг за другом,

имеет данный цвет. К примеру, монохромная картинка на условном экране размером 9 х 10 пикселей, изображённая на рисунке 6.2 (каждая клетка — это один пиксель), может быть представлена следующим сообщением:

4Б1 Ч8Б1Ч6Б1Ч1Б1 Ч6БЗЧ4Б.

а) Проверьте, что указанное сообщение действительно кодирует данное изображение.

б) Какое изображение кодируется на том же экране сообщением

4Б 1 Ч7БЗЧ7БЗЧ7БЗЧ7БЗЧ7БЗЧ5Б5Ч4Б5ЧЗБЗЧ 1 БЗЧ2БЗЧ 1 БЗЧ 1 Б? А сообщением

ЗБЗЧ5Б5ЧЗБ7Ч1 Б9Ч1 Б7Ч2Б2ЧЗБ2Ч2Б2ЧЗБ2Ч2Б2ЧЗБ2Ч2Б7Ч2Б

в) Нарисуйте какую-нибудь монохромную картинку на таком же экране (9 х 10 пикселей), закодируйте её соответствующим сообщением и предложите соседу по парте декодировать её. Если результат декодирования не совпал с исходным рисунком, выясните, кто из вас допустил ошибку.

Если каждый пиксель монохромного экрана кодируется 1 битом (1 — код белого цвета, О — код чёрного цвета), то информационный объём сообщения о картинке, изображённой на рисунке 6.2, составит 900 бит.

а) Какой объём имеет сообщение

4Б1Ч7БЗЧ5Б5ЧЗБ7Ч5Б1 Ч8Б1Ч8Б1 Ч8Б1 Ч 1 Б 1 Ч6БЗЧ4Б, которым представлена та же картинка, если считать, что каждая буква и каждая цифра в нём кодируется 1 байтом? Каков коэффициент сжатия при таком преобразовании исходного сообщения о состоянии данного монохромного экрана?

б) Поскольку используются только буквы Б и Ч и числа от 1

36

до 9, то каждую пару число — буква можно кодировать пятибитовой последовательностью, в которой первые четыре бита отведены под код цифры, а последний бит — это код цвета. Например, 4Б кодируется как 01000. Какой объём будет иметь сообщение после такой перекодировки? Чему в этом случае равен коэффициент сжатия по отношению к объёму первоначального сообщения о состоянии данного монохромного экрана?

Идея метода сжатия информации, высказанная в задании 9, носит название В1-Е-метода упаковки (от английского RunLength Encoding) ^[2] . Алгоритм сжатия сообщения методом RLE состоит в том, что каждая последовательность повторяющихся байтов заменяется двумя байтами: первый из них — управляющий — начинается с 1, а в остальных семи битах указано число (в двоичном виде) повторений байта из сообщения, второй байт — это точное воспроизведение повторяющегося байта. В начале каждой последовательности неповторяющихся байтов также добавляется управляющий байт, начинающийся с О, а в остальных семи битах указано число (в двоичном виде) неповторяющихся байтов. После такого управляющего байта воспроизводится цепочка неповторяющихся байтов. Например, в последовательности (для удобства байты в ней отделены друг от друга пробелом, в реальном сообщении пробелов, разумеется, нет)

1010100 10101010 11010100 11010100 11010100

следующий блок из трёх неповторяющихся байтов заменяется на 00000011101010101101010010101010, наконец, последний блок из трёх повторяющихся байтов заменяется на

щения:

Каков коэффициент сжатия для этого сообщения?

     б) После применения                        было получено сообщение

0101010101011010100.

Распакуйте это сообщение. Подсчитайте коэффициент сжатия. в) Используя  уменьшите объём сообщения, при-

ведённого в задании 15 из 6.1 (чтобы получить целое число байт, добавьте в конец этого сообщения ещё три 1).

г) После применения

Какой информационный объём имело исходное сообщение? Каков коэффициент сжатия?

д)* Как применить ВИЕ-метод, если количество идущих подряд одинаковых байт больше 127?

Алгоритм Хаффмана можно применить к любой битовой последовательности. Для этого последовательность разбивают на фрагменты и каждый получивший фрагмент рассматривают как код некоторого символа. Затем для этих «символов» применяют алгоритм Хаффмана и строят новый код. Если, например, последовательность

разбить на четырёхбитовые фрагменты, то получится следую-

4 раза), 1101 (встречается З раза), 0100 (встречается 2 раза), 010 («хвостик» из трёх бит — встречается 1 раз).

а) Постройте по этим данным код Хаффмана для указанного набора битовых фрагментов. Закодируйте этим кодом данную последовательность. Подсчитайте коэффициент сжатия.

б) Разбейте данное сообщение на трёхбитовые фрагменты и выполните те же задания, что и в пункте а.

в) Разбейте сообщение, приведённое в задании 15 из 6.1, на семибитовые фрагменты и выполните для него те же задания, что и в пункте а.

для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный код:

01, Б = 110, В = 101. Как нужно закодировать букву Г, чтобы длина кода этой буквы была минимальной, а любое сообщение, переданное в этом коде, допускало однозначное декодирование?

Основные информационные технологии

Под технологией обычно понимают процесс, обеспечивающий гарантированное получение нужного продукта из исходного материала. Информационная технология — процесс, использующий совокупность средств и методов обработки исходной информации для изменения её содержания или формы её представления.

7 Обработка текстовой информации

В информатике текстом принято называть любую последовательность знаков некоторого алфавита. Текст является носителем информации, но содержательное преобразование этой информации, как правило, не относят к обработке текста. Иными словами, под обработкой текста средствами информационной технологии обычно понимают такое его преобразование, которое не меняет, по существу, его информационное содержание. В ходе такой обработки исправляются орфографические, синтаксические и стилистические ошибки, удаляются ненужные повторы, вводятся уточняющие слова и т. п. Текст структурируется, т. е. разбивается на разделы (главы, параграфы, пункты) и абзацы. Наконец, в текст вставляются иллюстрации — чертежи, рисунки, диаграммы, графики и т. п. Структурные элементы текста тем или иным образом располагаются на странице — центрируются заголовки, определённым образом располагаются эпиграфы к главам или параграфам, 39

выравниваются (или, наоборот, не выравниваются) края текста, выделяются каким-либо образом основные положения и т. д.

О а) Наберите с помощью клавиатуры слова новогодней песенки «Ёлочка» (или какое-нибудь другое стихотворение, которое вы помните), причём заголовок наберите заглавными буквами и каждую строку начинайте тоже с заглавной буквы. Располагайте текст от левого края экрана. Используйте при работе вставку, удаление и т. д. Сохраните набранный текст в файле.

б) Отделите все строки друг от друга, вставляя каждый раз пустую строку.

в) Используя операцию разбиения строки, сделайте так, чтобы в каждой строке осталось только одно слово, и расположите эти слова «лесенкой» (как у Маяковского).

г) Соедините строки так, чтобы они стали такими, как до разбиения. Совпало ли то, что у вас получилось, с первоначально набранным текстом? (Для сравнения можно вызвать в другое окно текст, который вы сохранили, выполнив задание пункта а.)

Наберите текст детского стихотворения, не забывая в нужный момент переходить на латинский шрифт и обратно.

а) Я шалил: разбилась ваза. — Кто разбил? — спросил мой father.

— Это бабушкина ваза...,

Прослезилась моя mother.

Тут за меня вступилась sister:

 Осколки он убрал, всё чисто!

Потом сказала: «Father, mother,

Шалить не будет больше brother».

б) Ну, почему считает папа,

Что все медведи косолапы?

Нет, мой медведь не косолап, Я попросил его: «Stand ИР!»

Он встал... на две кривые лапы.

«Садись — sit down!» Прав мой папа...

О Наберите текст благодарственного письма от руководства школы вашим родителям. В оформлении можно следовать ниже приведённому образцу, заменяя слова, стоящие в скобках, на те, которые соответствуют, на ваш взгляд, действительности. Используйте шрифты различной гарнитуры и различного кегля.

БЛАГОДАРСТВЕННОЕ ПИСЬМО Уважаемые (имя и отчество родителей)! Дирекция (школы, лицея, гимназии) N2 (номер)  (название города) благодарит вас за воспитание вашего (сына, дочери), (фамилия, имя), которое выражается (в хорошей успеваемости, активной общественной деятельности, примерном поведении, добром отношении к товарищам      Директор (школы, гимназии, лицея) .N2       (номер)  (Ф.И.О.)

О Создайте таблицу, в которой бы хранилась информация о некоторых ваших друзьях-одноклассниках (например, по приведённому ниже образцу).

Фамилия и имя	Дата рождения	Адрес	Телефон	Имя и отчество родителей
Иванов Саша	13.03.88	ул. Гагарина, д. 15, кв. 107	777-77-77	Тамара Михайловна, Николай Фёдорович

Обработка числовой информации с помощью электронной таблицы

Одним из инструментов технологии обработки числовой информации являются электронные таблицы. Основное назначение электронной таблицы — обработка числовой информации, представленной в табличной форме, при этом часть информации является исходной (или, как говорят, независимой), другая — вычисляемой (зависимой). Вся информация в электронной таблице размещается в её ячейках, визуально представленных как клетки таблицы, образованные пересечением строк и столбцов. Столбцы электронной таблицы обычно поименованы буквами латин-

41

ского алфавита, а строки — перенумерованы. Каждая ячейка, тем самым, получает адрес, состоящий из обозначения столбца и номера строки.

В каждой ячейке может находиться либо текст, либо число, либо формула. Под формулой при этом понимается арифметическое выражение, содержащее числа, адреса ячеек (или их имена, если электронная таблица допускает именование ячеек), и встроенные функции (среди которых имеются логические, поэтому формула может иметь вид оператора ветвления), соединённые знаками арифметических операций. Набор встроенных функций, вообще говоря, для каждой электронной таблицы свой, но, как правило, среди них имеются функции вычисления квадратного корня, экспоненты и логарифма, тригонометрических функций, логических функций (и, или, не, если) и т. д. Кроме того, имеются функции, работающие с блоком ячеек. Таковым называют совокупность всех ячеек, составляющих некоторый прямоугольник. Блок ячеек обычно указывается адресом ячейки в верхнем левом углу и (через двоеточие) адресом ячейки в правом нижнем. К функциям, допускающим обработку блока ячеек, относятся функции нахождения суммы, среднего значения, произведения

Среди операций, которые можно выполнять над электронной таблицей, всегда присутствуют операции вставки и удаления строк и столбцов, копирования блока ячеек, очистка содержимого блока ячеек и т. п. При этом в электронной таблице действует так называемый принцип относительной адресации. Он означает, что адреса ячеек в формуле определены не абсолютно, а относительно той ячейки, где расположена формула. Поэтому при копировании содержимого ячейки или блока ячеек в другое место автоматически пересчитываются адреса ячеек, фигурирующих в формулах копируемого фрагмента. Таким образом, относительная адресация проявляет себя в том, что всякое изменение места расположения формулы приводит к автоматическому пересчёту адресов ячеек, фигурирующих в этой формуле.

Если же в копируемых формулах всё время должна использоваться одна и та же ячейка (например, в ней хранится нужная константа) или ячейки одной и той же строки, то адрес такой ячейки или соответственно номер строки помечается в формуле как абсолютный. Обычно для этого применяется зарезервированный символ (довольно часто знак $).

Одной из важных возможностей современных электронных таблиц является построение графиков и диаграмм по данным, рассчитываемым с помощью этой таблицы.

О Сколько ячеек содержит блок ЕЗ:Нб? А блок У7:АВ9?

О В некоторой ячейке электронной таблицы записано выражение: а)

Какое значение будет записано в этой ячейке?

О В ячейке А1 электронной таблицы требуется вычислить значение суммы чисел, стоящих в блоке ячеек от В2 до ЕВ. Какую формулу надо записать в ячейку А1?

о В электронной таблице значение формулы равно 2. Чему равно значение формулы =СУММ(Аб:Сб), если в ячейке D6 записано число —5?

В электронной таблице в ячейках А7, В7 и С7 записаны соответственно формулы =МИН(А1:Аб), =МИН(В1:В6), =МИН(С1:С6), а в ячейку 07 записана формула =МАКС(А7:С7). После того как в ячейке ВЗ записанное там число поменяли на 7, изменилось и число в ячейке D7. Можно ли по этой информации определить, какое число теперь оказалось в ячейке D7? Если можно, то укажите это число, если нет, то объясните почему.

О В ячейку В1 записана формула:

=ЕСЛИ (МИН(А1:А4) < О;

Определите, чему равно значение в ячейке В1, если о числах, записанных в ячейках А1—А4, известно, что:

а) их сумма равна —3, а произведение равно 12;

б) их сумма равна З, а произведение равно —6;

в) их сумма равна О, а произведение равно 4;

г)* их сумма равна 5, а произведение равно 2,5.

Первоначально ячейки электронной таблицы были заполнены числами так, как показано в таблице. Затем в ячейку А1 записали формулу =С$1 + $ВЗ и скопировали её в ячейку В2. Какое значение будет записано в ячейке В2?

					11
				12	8
5	2	6	4	2	1

О дан фрагмент таблицы в режиме отображения формул. Затем формула из ячейки А5 была скопирована в ячейки Аб, В5 и Вб. Какое значение окажется в ячейке Вб после того, как будут выполнены вычисления?

		в
1	1	2
2	2	4
з	з
4	4	8
5

О а) С помощью электронной таблицы составьте для аргумента х, меняющегося на отрезке от —3 до 2 с шагом 0,1, таблицу значений функции у = .r⁴ + 6х3 + 2х2— 18х + 4.

б) Используя составленную таблицу значений, постройте с помощью электронной таблицы график этой функции. для каждого из корней уравнения х^а + 6х³ + 2х² — 18х О, имеющихся на отрезке от —3 до 2, определите промежутки, на которых они находятся.

в) Используя режим «Подбор параметра», найдите все корни уравнения у= х⁴ + 6х³ + 2х² — 18х + О, расположенные на отрезке от —3 до 2. Точность корня должна быть не менее 0,001. г) У этого уравнения имеется корень, расположенный за пределами отрезка [—3; 2]. Найдите этот корень с точностью до 0,001.

С помощью электронной таблицы найдите с точностью до 0,001 все решения уравнения х = З cos х.

а) Требуется найти максимальное значение выражения 5х² — бу² для тех положительных чисел х и у, которые удовлетворяют неравенствам х— 2у < 4, 2ху>7, х + у < 100. С помощью электронной таблицы решите эту задачу. (С ов е т: воспользуйтесь надстройкой «Поиск решения».)

9 Базы данных и информационнопоисковые системы

База данных — организованная совокупность данных, предназначенная для длительного хранения во внешней памяти компьютера и многократного использования.

Каждая база данных состоит из двух компонентов: содержимого и программной оболочки. Оболочка представляет постоянную часть базы данных и предназначена для обработки содержимого базы. Эту оболочку обычно называют системой управления базой данных (СУБД). Система управления базой данных играет роль, аналогичную языку программирования. Можно считать, что это некоторая система команд, обеспечивающая организацию данных и манипулирование с ними. Главная функция СУБД — давать ответы на запросы пользователя, иными словами, удовлетворять его информационную потребность. Кроме того, СУБД позволяет изменять (как говорят, редактировать) записи, хранящиеся в базе данных, вносить новые сведения и выполнять другие операции над данными, например упорядочивать их по значениям заданного атрибута (так называемый режим сортировки данных).

Каждая база данных ориентирована на определённую предметную область, в рамках которой рассматриваемые в ней объекты или явления характеризуются конкретным набором свойств, или, как говорят в теории баз данных, набором атрибутов (полей).

Некоторые из атрибутов (полей) могут быть объявлены ключевыми. По таким атрибутам можно, в частности, делать сортировку.

По способу организации связей между атрибутами различают три вида баз данных: иерархические, реляционные и сетевые. В иерархических базах данных атрибуты соподчинены между собой так, что данные образуют древовидную структуру.

Сетевая база данных представляет собой более общую структуру, нежели иерархическая база, — в ней элементы связаны не только от одного уровня к следующему, а, вообще говоря, произвольным образом.

Реляционная база данных — это совокупность связанных между собой таблиц, столбцы которых задаются атрибутами данных, а каждая строка состоит из значений атрибутов для конкретного объекта.

Разновидностью баз данных являются информационно-поисковые системы (ИПС). Так обычно называют базы данных, в которых пользователю предоставляется возможность лишь получать ответы на запросы, при этом форма запросов фиксирована разработчиками и тоже не может изменяться пользователем.

О Что такое база данных? Что такое СУБД?

для чего предназначена операция сортировки в БД?

В ИПС «Государства» хранятся следующие сведения о государствах Европы:

•    название государства — атрибут Название;

•    площадь, км² — атрибут Площадь;

•    население, тыс. чел. — атрибут Население;

•    название столицы — атрибут Столица;

•    наименование денежной единицы — атрибут Деньги;

•    государственный язык — атрибут Язык;

•    форма государственного устройства — атрибут Правление;

•    вхождение в военно-политический или экономический блок (НАТО, ЕЭС и т. п.) — атрибут Блок.

В запросе к этой ИПС указывается название атрибута и значения, по которым требуется провести поиск. Отношения между атрибутом и значением описываются знаками =, % а для атрибутов с числовыми значениями могут также использоваться знаки >, <, >= и е. Например, чтобы найти все страны с населением больше 100 000 человек, составляется запрос Население > 100, а для нахождения стран с парламентской формой правления, не входящих ни в какие блоки, потребуется запрос Правление = “парламентская республика“ и Блок = ”нет”. Составьте запросы, позволяющие найти

а) все страны-карлики (площадь меньше 50 000 км ² );

б) все страны, которые не пользуются евро в качестве государственной валюты;

в) все страны с площадью более 10 ООО км ² и населением менее 1 млн человек;

г) все страны с населением больше 2 млн человек, кроме франкоговорящих;

д) все страны ЕЭС, не входящие в НАТО;

е) все европейские монархии (напомним, что в Европе есть четыре вида монархий: абсолютная, конституционная, парламентская и княжеская).

О Какой запрос ИПС «Государства» (см. задание З) надо сформулировать, чтобы выяснить:

а) все ли государства с населением больше 1 млн человек входят в ЕЭС;

б) во всех ли государствах, входящих в ЕЭС, проживает больше 1 млн человек?

Однажды школьник решил воспользоваться ИПС «Государства» (см. задание З), чтобы найти все конституционные и абсолютные монархии. С этой целью он составил следующий запрос: Правление = ”Конституционная монархия” и Правление = ”Абсолютная монархия”.

В ИПС не оказалось стран, удовлетворяющих этому запросу. Объясните почему. Какой запрос надо составить, чтобы получить нужную школьнику информацию?

О База данных о поступивших в магазин фруктах представлена таблицей

п/п	Товар	Страна	Цена	Общий вес
1	Мандарины	Пакистан	57	200
2	Апельсины	Марокко	38	450
З	Ананасы	Мадагаскар	65	450
4	Апельсины	Испания	42	450
5	Киви	Индонезия	33	250
6	Маракуйя	Алэкир	112	200
7	Киви	Бразилия	35	350
8	Бананы	Индонезия	28	200
9	Мандарины	Алжир	48	350

Данная база была отсортирована по следующему принципу: сначала по возрастанию поля Количество, затем для одинаковых значений в поле Количество — по убыванию поля Товар, затем для одинаковых значений в поле Товар — по возрастанию поля Цена. Какой товар окажется в строке под номером 6?

Представьте, что вы руководитель небольшой фирмы. Вам необходимо иметь ту или иную информацию о своих работниках. Разработайте двухтабличную базу данных: одна таблица — «Штатное расписание» — содержит информацию о должностях, окладах, отделе, которому приписана данная должность; другая таблица — «Сотрудники» — содержит информацию о работающих у вас сотрудниках (дата приёма на работу, образование, дата рождения), об их должностях и рабочем месте (название отдела, номер комнаты, рабочий телефон). Свяжите эти таблицы по подходящему ключевому атрибуту. С помощью данной базы данных получите ответы на вопросы:

а) У кого из сотрудников имеется высшее образование?

б) Кто самый молодой сотрудник вашей фирмы?

в) Какие вакансии (т. е. незанятые должности) имеются в вашей фирме?

г) Кто из работников в этом году начнёт получать пенсию по старости (женщины выходят на пенсию в 55 лет, а мужчины — в 60)?

д) У кого из сотрудников вашей фирмы стаж работы не меньше 10 лет?

е) Вам срочно потребовалась консультация одного из ваших специалистов, а у него сегодня выходной. Найдите номер его домашнего телефона (заодно узнайте его имя и отчество).

ж) К празднику 8 Марта вы решили лично поздравить женщин — начальников отделов вашей фирмы. Поручите СУБД представить вам нужный список.

Ваша фирма (см. задание 7) ведёт активную работу с иногородними клиентами. Поэтому ваши сотрудники ведут много междугородних переговоров. Прежде всего это сотрудники отделов сбыта и рекламы, но не исключено, что и у сотрудников других отделов (например, бухгалтерии) тоже возникает необходимость в телефонных переговорах. Информация о всех состоявшихся телефонных звонках ежемесячно поступает из телефонной компании: сообщается дата, номер телефона, продолжительность разговора и пункт, с которым вёлся телефонный разговор. Дополните уже разработанную вами базу данных таблицей о телефонных разговорах с указанной информацией. Установите связь новой таблицы с уже имеющимися. Создайте запросы и выполните действия, позволяющие получить ответы на следующие вопросы:

а) С какими пунктами вёл телефонные переговоры ваш отдел сбыта?

б) В какие дни были переговоры с нужным вам пунктом и кто из сотрудников эти переговоры вёл?

в) Велись ли с телефонов вашей фирмы неслужебные разговоры (т. е. с пунктами, в которых нет ваших партнёров и клиентов) и кто из сотрудников такие разговоры вёл?

г) С каким из клиентов переговоры были наиболее интенсивными (по количеству переговоров за месяц)?

д) С каким из клиентов переговоры были наиболее продолжительными (по суммарному времени всех переговоров за месяцр

1 О Понятие алгоритма и исполнителя.

Линейные алгоритмы

Алгоритм — приводящая к определённому результату последовательность действий, допустимых для некоторого исполнителя.

Исполнитель — субъект или объект, выполняющий действия согласно предписанной ему инструкции. Исполнитель может быть формальным или эвристическим. Формальный исполнитель выполняет инструкцию, не вникая в её смысл и не принимая во внимание цель, с которой она составлена. Эвристический исполнитель согласовывает свои действия с целевыми установками и принимает решение о том, как выполнить то или иное действие, сообразуясь со смыслом инструкции.

Каждый исполнитель полностью характеризуется своим набором допустимых действий и средой, в которой он существует.

Запись алгоритма состоит из команд, каждая из которых указывает исполнителю, какое допустимое действие тот должен совершить, получив эту команду. Набор всех команд исполнителя называется системой команд исполнителя (СКИ). Кроме этого, в записи алгоритма присутствуют операторы алгоритмических конструкций, определяющие порядок выполнения команд алгоритма. При отсутствии таких операторов команды, из которых составлен алгоритм, будут исполняться одна за другой в порядке их записи в алгоритме. Такой алгоритм называется линейным.

В записи алгоритма могут присутствовать комментарии, поясняющие человеку, читающему данный алгоритм, для чего предназначено данное действие в алгоритме. Комментарии в записи алгоритма условимся выделять круглыми скобками со звёздочками, например: ( * комментарий *).

Среда исполнителя — это совокупность объектов и связей между ними, над которыми данный исполнитель может совершать допустимые для него действия.

Совокупность тех результатов, которые можно получить с помощью данного исполнителя, называется его достижимыми целями.

О Попытайтесь определить, что является средой для:

а) системы управления базами данных;

б) станка с числовым программным управлением;

в) автопилота;

г) графического редактора;

д) программируемого видеомагнитофона.

О Насколько можно говорить о том, плох формальный исполнитель или хорош? Например, что означает фраза «Я недоволен электронной таблицей»? Означает ли это, что формальный исполнитель не справляется с предназначенными для него алгоритмами?

О а) В приведённых ниже примерах укажите преимущественный, на ваш взгляд, вид обработки информации — алгоритмический или эвристический:

о вывод формулы корней кубического уравнения;

•   определение кислотности среды с помощью лакмуса;

•   определение очередного хода в середине шахматной партии; о определение величины сопротивления цепи электрического тока при наличии амперметра и вольтметра; в нахождение корней кубического уравнения по заданным формулам.

б) Проанализируйте свою обычную ежедневную деятельность по обработке информации. С каким видом обработки — алгоритмическим или эвристическим — вам чаще приходится иметь дело? Проанализируйте с той же точки зрения вашу учебную деятельность на уроках по разным предметам.

О Пусть дан угол АВС (В — вершина угла, А и С — точки на сторонах угла). Определите, для решения какой задачи предназначен следующий алгоритм:

Поставить ножку циркуля в точку В.

4— Гейн. Задачник-практикум, 10—11

Установить раствор циркуля равным длине отрезка ВА.

Провести окружность.

Поставить ножку циркуля в точку пересечения этой окружности с лучом ВС. Провести окружность.

Поставить ножку циркуля в точку А.

Провести окружность.

Провести прямую через точку В и вторую точку пересечения тех же окружностей.

Робот записывает цепочки символов. Каждая цепочка записывается в отдельную строку. Первая строка содержит цепочку из четырёх цифр: 1357. Каждая последующая строка содержит цепочку, которая получается из предшествующей цепочки по следующему правилу: записывается предшествующая цепочка и к ней справа приписывается такая же цепочка, но в которой каждый символ дважды подряд повторяется, затем последний символ заменяется на номер строки. Вот первые три строки: 1357

135711335572

а) Какая пара цифр будет стоять на 999-м и 1000-м местах в цепочке, записанной в шестой строке?

б) Какая пара цифр будет стоять на 9999-м и 10 000-м местах в цепочке, записанной в девятой строке?

О а) Имеется два кувшина ёмкостью 7 и 12 литров, Исполнитель ВОДОЛЕЙ может набирать воду из реки в каждый кувшин, выливать из него воду и определять, налита ли вода в кувшине доверху. Составьте алгоритм, выполнив который ВОДОЛЕЙ наберёт из реки 10 литров воды.

б) Может ли ВОДОЛЕЙ набрать 7 литров, если в его распоряжении два кувшина ёмкостью 6 и 10 литров?

в)* Имеется два кувшина ёмкостью а литров и Ь литров (а и Ь — натуральные числа). Исполнитель ВОДОЛЕЙ может набирать воду из реки в каждый кувшин, выливать из него воду и определять, налита ли вода в кувшине доверху. Результатом работы исполнителя ВОДОЛЕЙ является количество воды, которое он может получить в меньшем по ёмкости кувшине. Укажите достижимые цели для данного исполнителя в зависимости от исходных значений а и Ь.

О Имеется три кувшина ёмкостью 4, 9 и 15 литров. С ними управляется исполнитель ВОДОЛЕЙ, который описан в задании 6. Составьте алгоритм, выполнив который ВОДОЛЕЙ наберёт из реки 11 литров воды.

О а) На клетчатой бумаге изображено несколько многоугольников, вершины которых располагаю^тс^я в вершинах клеток (рис. 10.1). Составьте для каждой из ^этих фигур алгоритм

       а)                                б)                                в)

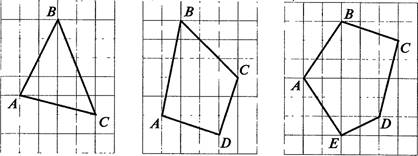
Рис. 10.1

нахождения с помощью карандаша и линейки без делений центра тяжести фигуры. (Совет: воспользуйтесь тем, что центр тяжести треугольника — это точка пересечения его медиан.) б) Составьте алгоритм нахождения с помощью карандаша и линейки без делений центра тяжести любого треугольника, изображённого на клетчатой бумаге так, что его вершины располагаются в вершинах клеток.

в) Нарисуйте на клетчатой бумаге какой-либо треугольник, вершины которого располагаются в вершинах клеток. Предложите соседу по парте найти центр тяжести треугольника с помощью составленного им алгоритма. Проверьте правильность исполнения алгоритма и правильность результата.

О Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены стены. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение алгоритма прервётся.

а) Робот, начав с некоторой клетки, успешно исполнил следующий алгоритм:

влево влево вверх вправо вниз вверх вправо

Составьте алгоритм, содержащий наименьшее число команд, после исполнения которого Робот не разрушится и вернётся из той клетки, в которой оказался, в исходную клетку.

б) Выполните задание, аналогичное пункту а, для следующего алгоритма:

вправо вниз вправо вниз влево вверх влево вниз влево вверх вправо влево вверх

Исполнитель умеет умножать число на З и увеличивать число

а) Составьте для этого исполнителя алгоритм получения числа 1000 из единицы.

б) Сколько действий в самом коротком из таких алгоритмов? Ответ обоснуйте.

Исполнитель умеет умножать число на З и уменьшать число

а) Составьте для этого исполнителя алгоритм получения числа 2000 из единицы.

б) Сколько действий в самом коротком из таких алгоритмов? Ответ обоснуйте.

Исполнитель КВАДР имеет два допустимых действия:

а) возвести число, записанное на табло исполнителя, в квадрат;

б) вычесть З из числа, записанного на табло исполнителя.

После исполнения каждого действия на табло записывается результат. Команду на исполнение первого действия будем обозначать К, второго — В. Последовательность КВ означает, что сначала число возводится в квадрат, а из результата вычитается З; запись ВК означает, что сначала из числа вычитается З, а затем результат возводится в квадрат.

а) Составьте для этого исполнителя алгоритм получения числа 34 из числа 5.

б) Сколько действий в самом коротком из таких алгоритмов? Ответ обоснуйте.

 Алгоритмические конструкции

Среда, в которой действует исполнитель, может накладывать ограничения на возможность выполнения того или иного действия или последовательности действий. Чтобы исполнитель мог учитывать обстановку, сложившуюся в окружающей его среде, в том ^числе и в результате его

собственных действий, в число допустимых действий исполнителя должны входить действия по проверке условий, относящихся к обстановке, имеющейся к данному моменту в среде, где находится исполнитель. Если условие выполнено, то исполнитель осуществляет некоторую последовательность действий, если же условие не выполнено, то эта последовательность действий не исполняется, а исполнитель либо совершает другую последовательность действий, либо вообще переходит к исполнению действий, предусмотренных алгоритмом после первой последовательности. Конструкция, реализующая в алгоритме указанную возможность выбора исполняемой последовательности действий в зависимости от условия, называется ветвлением.

Кроме того, к ветвлениям относится и конструкция выбор. Суть этой конструкции состоит в том, что в зависимости от значения условия-селектора исполняется та последовательность действий, которая помечена данным значением.

В алгоритмах мы будем записывать ветвление в одной из двух форм:

Если (условие) то { действие; действие• ...} — неполная форма ветвления, или

Если (условие) то { действие; действие ...} иначе { действие; действие — полная форма ветвления.

Фигурные скобки показывают, какая последовательность действий исполняется, если условие выполнено — она записана после слова уд, и какая исполняется, если условие не выполнено — эта последовательность записана после слова иначе. Фигурные скобки, используемые для обрамления группы действий в алгоритме, называют операторными скобками.

В записи алгоритма конструкцию выбор договоримся оформлять так:

Выбор при (условие 1): { действие; действие } при (условие_2): { действие; действие }

др.! (условие_п): { действие; действие; .. } иначе { действие; действие

Ветвь, начинающаяся словом иначе, может отсутствоваты

Нередко исполнителю необходимо повторить несколько раз какую-либо последовательность действий. То, сколько раз придётся повторить данную последовательность,

может быть известно заранее, а может определяться выполнением условия, которое проверяется каждый раз перед выполнением последовательности действий или сразу после этого.

Алгоритмическая конструкция, позволяющая указать исполнителю на повторяемость последовательности действий, называется циклом. Последовательность действий, которую исполнитель будет выполнять в цикле, называется телом цикла.

Основные виды циклов: цикл простого повторения (цикл повторить п раз), цикл с предусловием (цикл пока), цикл с постусловием (цикл до), цикл со счётчиком (цикл от... до... с шагом...). Вид цикла указывается в его заголовке.

Цикл с предусловием — это цикл, в котором действия, составляющие тело цикла, исполняются, пока остаётся истинным условие, записанное в заголовке цикла. В алгоритмах цикл с предусловием будем записывать в следующей форме:

Делать пока (условие)

{ действие; действие;

Цикл с постусловием — это цикл, в котором действия, составляющие тело цикла, исполняются, пока не станет истинным условие, записанное в окончании цикла. В алгоритмах цикл с постусловием будем записывать в следующей форме:

Повторять

{ действие; действие;

(условие);

В качестве условия обычно используется какое-либо высказывание, проверка истинности которого является допустимым действием исполнителя. В цикле с предусловием эта проверка осуществляется всегда перед началом очередного исполнения тела цикла, а в цикле с постусловием всегда после очередного исполнения тела цикла и никогда не совершается во время исполнения тела цикла (даже если в результате исполнения какого-либо действия высказывание становится ложным).

Две указанные формы цикла с условием полностью взаимозаменяемы, т. е. использование одного из них мо-

жет быть заменено другим. Однако при решении задач на алгоритмизацию нужно стараться выбрать ту форму, которая более естественна (например, приводит к выполнению исполнителем меньшего числа действий).

В записи алгоритма конструкцию цикл повторить п раз договоримся оформлять так:

Повторить п раз

{ действие; действие;

Здесь п — числовая переменная целого типа либо арифметическое выражение, значение которого также имеет целый тип (см. п. 12.1). Некоторые языки программирования допускают в качестве ограничителя п числовую переменную и вещественного типа; в этом случае тело цикла исполняется [п] раз. ^[3]

Цикл со счётчиком — это цикл, в котором известно, сколько раз нужно исполнить тело цикла, причём значение счётчика влияет на исполнение действий в теле цикла. В алгоритмах цикл со счётчиком будем записывать в следующей форме:

Делать от К := ...с шагом ...

{ действие; действие;

Здесь К — числовая переменная (см. п. 12.1); после

знака :=, слов де и с шагом могут стоять числовые константы или арифметические выражения. Слова с шагом могут отсутствовать; в этом случае после очередного исполнения тела цикла значение переменной К автоматически увеличивается на 1. Тело цикла исполняется до тех пор, пока значение переменной К не станет больше константы или значения арифметического выражения, стоящего после слова И.

Чтобы наглядно представлять формы организации действий, используют так называемые схемы.

Достаточно часто внутри одной алгоритмической конструкции может потребоваться использование одной или нескольких других алгоритмических конструкций. Такие конструкции называются вложенными друг в друга.

О Составьте алгоритм размена суммы денег (К рублей) двух- и пятирублёвыми монетами.

Составьте алгоритм, который по запрашиваемой оценке в баллах сообщил бы её словесный эквивалент: о 1 балл — плохо;

•   2 балла — неудовлетворительно; • З балла — удовлетворительно; о 4 балла — хорошо;

•   5 баллов — отлично.

О а) Составьте алгоритм, который по запрашиваемому номеру месяца сообщал бы количество дней в этом месяце (для невисокосного года).

б) Составьте алгоритм, который по запрашиваемому номеру месяца и номеру года сообщал бы количество дней в этом месяце.

О Робот перемещается по клетчатому полю, переходя из клетки в соседнюю клетку по соответствующей команде: вверх, вниз, вправо, влево. Между некоторыми клетками поля установлены стены, сквозь которые Робот пройти не может. Робот умеет также проверять истинность условия отсутствия стены у каждой стороны той клетки, где он находится. Если Робот попытается пройти сквозь стену, то он разрушится и исполнение программы прервётся.

а) Робот исполняет следующий алгоритм, находясь на поле, изображённом

Рис. 11.1                             на рисунке 11.1.

Алгоритм

{ Делать пока (це снизу стена)

{ Вниз;

Вправо;

Делать пока (це сверху стена) { Вверх;

Вправо;

длиной пути Робота считается количество переходов из клетки в соседнюю клетку при успешном завершении исполнения алгоритма. Робот может начать исполнение алгоритма с лю-

б)

аввваав

6

5

4 З

2

1

        A B C D E F G  A B C D E F G

Рис. 11.2

бой клетки поля. Укажите, для какой начальной клетки путь робота окажется самым длинным.

б) Выполните то же задание, что и в пункте а, для полей, изображённых на рисунке 11.2.

в) Нарисуйте своё поле тех же размеров, но с иным расположением стен. Предложите соседу по парте выполнить то же задание, что и в пункте а, на придуманном вами поле. Проверьте его ответ.

а) На поле, изображённом на рисунке 11 .З, Робот, описанный

в задании 4, исполняет следующий алгоритм:

Алгоритм

{ Повторить К рад { Вверх;

Повторить т раз { Влево;

Повторить п раз

{ Вниз;

A B C D E F

Повторить s раз

Рис. 11.3

{ Вправо;

Какое наибольшее значение может иметь сумма К + т + п + s, для которой Робот, начав исполнение предложенного алгоритма с подходящей клетки, успешно его закончит? для этого значения суммы укажите клетку, с которой Робот должен начать исполнение алгоритма.

б) Выполните то же задание, что и в пункте а, для полей, изображённых на рисунке 1 1.4.

а)

6

5 4

З

2

1

          A B C D E F A B C D E F

Рис. 11.4

О На поле, изображённом на рисунке 11 .З, Робот, описанный в задании 4, исполняет следующий алгоритм:

Алгоритм

{ Повторить раз

{ Вверх;

Повторить т раз

{ Влево;

Повторить п раз

{ Вниз;

Повторить s рад

{ Вправо;

Какое наибольшее значение может иметь сумма К + т + п + s, для которой Робот, начав исполнение предложенного алгоритма с подходящей клетки, успешно его закончит? для этого значения суммы укажите клетку, с которой Робот должен начать исполнение алгоритма.

а) На поле, изображённом на рисунке 1 1.5, Робот, описанный в задании 4, исполняет следующий алгоритм:

Алгоритм

{ Делать пока (цд справа стена)

{ Вверх;

Делать пока (це сверху стена)

{ Влево;

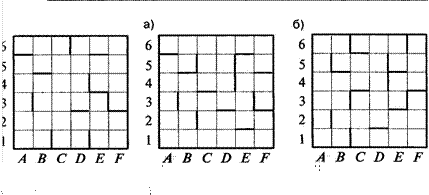
Делать пока (не слева стена) { Вниз;

Делать пока (це внизу стена)

{ Вправо;

Перечислите те клетки лабиринта, для которых Робот, исполнив предложенный алгоритм, уцелеет и остановится в той же клетке, с которой он начал движение.

б) Выполните то же задание, что и в пункте а, для полей, изображённых на рисунке 1 1.6.

О На поле, изображённом на рисунке 11 .7, Робот, описанный в задании 4, исполняет следующий алгоритм:

Алгоритм

{ Делать пока (цд сверху стена)

{ Вверх;

                Если (це справа стена)          { Вправо;

                Если (цд снизу стена)         { Вниз; }

Если (ЦД слева стена) !..g { Влево; }

а) для каждой клетки первого ряда укажите, в какой клетке окажется Робот после исполнения данного алгори1, а.

б) Имеются ли на этом поле жизненно опасные кле^т ки, т. е. такие клетки, начав с КОТОРЫХ Робот разобьётся при исполнении данного алгоритма?

в) Перечислите те клетки данного поля, начав с которых Робот никогда не закончит исполнение данного алгоритма.

60

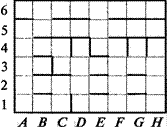         A B C D E F G

                                              Рис. 11.8

г) Выполните задания, сформулированные в пунктах а и в, для поля, изображённого на рисунке 1 1.8.

На поле, изображённом на рисунке 1 1 .7, Робот, описанный в задании 4, исполняет следующий алгоритм:

Алгоритм

{ Делать пока (цд сверху стена)

{ Верх;

Если (це слева стена) то { Влево; }

Делать пока (це справа стена) { Вправо;

Если (не внизу стена) то { Вниз;

а) для каждой клетки первого ряда укажите, в какой клетке окажется Робот после исполнения данного алгоритма.

б) Перечислите те клетки, начав с которых Робот никогда не закончит исполнение данного алгоритма.

в) Выполните задания, сформулированные в пунктах а и б, для поля, изображённого на рисунке 1 1.8.

Имеется полоска клетчатой бумаги шириной в 1 клетку и длиной в п клеток. Робот может закрасить клетку, на которой он находится, в красный, жёлтый или зелёный цвет (не важно, каким цветом была клетка закрашена до этого), а также переместиться на одну клетку вправо или влево. Робот умеет также проверять, какого цвета клетка, на которой он находится, и не закончилась ли полоска. Если Робот стоит у края полоски и получает команду переместиться за край, то он выходит из строя. Робот стоит на самой левой клетке и исполняет следующий алгоритм:

Ы

Алгоритм

{ Если (находится на зелёной клетке) то

{ Закрасить клетку в жёлтый цвет;

Делать пока (находится не на зелёной клетке и справа не край полоски)

{ Перейти вправо;

Делать пока (находится на зелёной клетке и слева не край полоски)

{ Закрасить клетку в жёлтый цвет;

Перейти влево;

Если (находится на жёлтой клетке и справа не край полоски) то

{ Закрасить клетку в красный цвет;

Перейти вправо;

Делать пока (находится на красной клетке и слева не край полоски) то

{ Закрасить клетку в зелёный цвет;

Перейти влево;

Перейти влево;

а) Пусть п = 11 и первоначально клетки полоски (по порядку слева направо) закрашены так: зелёная, жёлтая, красная, жёлтая, красная, зелёная, зелёная, жёлтая, красная, жёлтая, зелёная. Сколько красных, жёлтых и зелёных клеток будет в полоске после исполнения данного алгоритма?

б) Пусть первоначально вся полоска закрашена красным цветом. Сколько красных, жёлтых и зелёных клеток будет в полоске после исполнения данного алгоритма?

в) Пусть первоначально вся полоска закрашена зелёным цветом. Сколько красных, жёлтых и зелёных клеток будет в полоске после исполнения данного алгоритма?

г) Пусть первоначально вся полоска закрашена жёлтым цветом. Сколько красных, жёлтых и зелёных клеток будет в полоске после исполнения данного алгоритма?

д) Придумайте свою раскраску полоски. Предложите соседу по парте выяснить, сколько красных, жёлтых и зелёных клеток будет в полоске после исполнения данного алгоритма при предложенной вами исходной раскраске. Проверьте его ответ.

62

О* Автомат за один шаг преобразует данное ему натуральное число следующим образом: если число делится на З, то он делит его на З, в противном случае вычитает из него 1. Сколько существует натуральных чисел N, каждое из которых данный автомат за 10 последовательных шагов превратит в 1?

 Переменные в алгоритмах

12.1. Переменные числового типа

Выражение, в котором фигурируют константы и переменные только числовых типов, называется арифметическим. При вычислении значения арифметического выражения действуют стандартные правила, устанавливающие старшинство операций: первой выполняется возведение в степень, затем умножение и деление и, наконец, сложение и вычитание.

В таблицах приведены обозначения операций, принятые в большинстве языков программирования, их взаимодействие с типами переменных, а также обозначения стандартных функций.

Обозначение основных операций

Операция	Выражение	Типы операндов	Тип результата
Сложение		Оба целые	Целый
		Хотя бы один вещественный	Вещественный
Умножение		Оба целые	Целый
		Хотя бы один вещественный	Вещественный
Вычитание		Оба целые	Целый
		Хотя бы один вещественный	Вещественный
Деление		Целый или вещественный	Вещественный
Целое деление	А div В	Оба целые	Целый
Остаток при целом делении	А mod В	Оба целые	Целый

Обозначения стандартных функций1

Функция	Обращение	Тип аргумента	Тип результата
Квадрат	sqr(x)	Целый или вещественный	Вещественный
Корень квадратный	sqrt(x)	Целый или вещественный	Вещественный
Синус	sin(x)	Целый или вещественный (в радианах)	Вещественный
Косинус	cos(x)	Целый или вещественный (в радианах)	Вещественный
Арктангенс	arctan(x)	Целый или вещественный	Вещественный
Экспонента (показательная функция)	ехр(х)	Целый или вещественный	Вещественный
Логарифм натуральный	ln(x)	Целый или вещественный	Вещественный
Модуль аргумента	abs(x)	Целый	Целый
		Вещественный	Вещественный
Округление	round(x)	Вещественный	Целый
Дробная часть	frac(x)	Целый или вещественный	Вещественный
Случайное число в интервале [О; 1)	random		Вещественный

1

В таблице приведены обозначения стандартных функций, принятые в Турбо Паскале. Если учащиеся изучают другой язык программирования, то при выполнении заданий данного и последующих параграфов следует использовать обозначения того языка, который реально изучается. Ввиду возможных разночтений мы, в частности, в записях алгоритмов с переменными не придерэкиваемся строго правил какого-либо языка программирования, а используем общеупотребительную математическую запись.

Продолжение

Функция	Обращение	Тип аргумента	Тип результата
Случайное целое число из интервала [О; х)	random(x)	Целый	Целый
Целая часть	int(x)	Целый или вещественный	Целый

О В К-этажном доме т подъездов, по п квартир в каждом. Составьте алгоритм, позволяющий по номеру квартиры определить подъезд и этаж, где располагается данная квартира. Значения К, т и п запрашиваются у пользователя.

О Банкомат выдаёт запрашиваемую сумму банкнотами достоинством в 50, 100, 500 и 1000 рублей. Составьте алгоритм, позволяющий по запрашиваемой сумме S определить, сколько банкнот каждого достоинства надо выдать, если выдача происходит начиная с самых крупных купюр, а сумма S всегда кратна 50.

О дан алгоритм, схема которого изображена на рисунке 12.1.

Какой результат будет выведен после исполнения этого алгоритма, если в качестве начальных значений будут введены следующие наборы чисел:

          а) х = 2, у = 0, z=3;              б) х = 1, у = 2, z=O;

О а) На координатной плоскости начерчена некоторая фигура. дан алгоритм, позволяющий распознавать, принадлежит ли этой фигуре точка с координатами (х; у): Алгоритм Распознавание 1

д.ещ: ^х , и;

{ Запросить х;

Запросить у;

Если ((х² + у² < 25) щ (х —3) щ (х < 4)) т.д { Сообщить ” Точка с координатами ( х принадлежит фигуре ” ,

Найдите площадь фигуры.

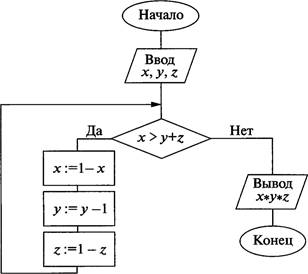
Рис. 12.1

б) Выполните такое же задание, как в пункте а, при следующем алгоритме распознавания: Алгоритм Распознавание 2

Д.е.щ: х, у, г;

{ Запросить х; Запросить у; г := х² + у² ,

Если (г < 4х) щ (г > 2х) то

{ Сообщить ”Точка с координатами (” , х, принадлежит фигуре '

 Составьте алгоритм решения уравнения а 1 х! + Ь = О; значения а и Ь запрашиваются у пользователя.

О а) Составьте алгоритм, при исполнении которого будет запрошено 4 числа и сообщено наибольшее и наименьшее из них.

б) Составьте алгоритм, при исполнении которого будет запрошено 4 числа и сообщено, образуют ли эти числа арифметическую прогрессию.

Составьте алгоритм, при исполнении которого будет запрошено З числа и сообщён периметр треугольника, для которого эти

5— Гейн. Задачник-практикум, 10—11

З числа являются длинами сторон. Если треугольника с такими сторонами не существует, об этом нужно сообщить.

Последовательность значений переменной Х строится так: х— 1; Х2=з; хп=2Хп-а-зхп 1

для каждого п > 2.

а) Чему равны Хз; Х4; Х7?

б) Составьте алгоритмы:

о нахождения первого значения, большего 1000;

• нахождения суммы первых 30 значений переменной Х; о нахождения первых десяти положительных значений переменной Х; о нахождения наибольшего из первых 50 значений переменной х.

в) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их.

Составьте алгоритм, при исполнении которого будет запрошено натуральное число и сообщена сумма кубов его цифр. Напишите на изучаемом вами язьке программирования программу, реализующую этот алгоритм, и отладьте её.

дано натуральное число п. Требуется переставить цифры этого числа так, чтобы получилось наибольшее возможное число. Составьте алгоритм, решающий эту задачу. Напишите на изучаемом вами языке программирования программу, реализующую этот алгоритм, и отладьте её.

Простым называется натуральное число, имеющее ровно два делителя.

а) Составьте алгоритм, при исполнении которого будет запрошено натуральное число п и сообщён его наименьший простой делитель. (Сов е т: обдумайте случай, когда исходное натуральное число равно 1.)

б) Напишите на изучаемом вами язьке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Проведите вычислительный эксперимент для п = 637; 4937; 51 983; 1 192 463.

Евклид доказал, что простых чисел бесконечно много.

а) Пусть все простые числа занумерованы в порядке возрастания. Составьте алгоритм, при исполнении которого будет сообщено простое число, имеющее номер п. Значение п запрашивается у пользователя.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Проведите вычислительный эксперимент для п = 20; 300; 7000; 10 000.

          в)                Пусть р (п) — простое число, имеющее номер п. Ис-

п ln п для п от 3000 до 100 ООО.

Математики доказали, что значение этой фунщии с ростом п всё меньше отличается от 1. Наблюдается ли это явление в вашем компьютерном эксперименте?

а) До сих пор неизвестно, конечно ли количество простых чисел, которые лишь на единицу отличаются от квадрата натурального числа. Таких чисел, меньших 100, всего 4. Вот они: З, 5, 17, 37. Составьте алгоритм, при исполнении которого будет сообщено, сколько имеется таких простых чисел, не превосходящих число п. Значение п запрашивается у пользователя. (Со вет: обдумайте, много ли существует простых чисел, которые на единицу меньше квадрата целого числа.) б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Проведите вычислительный эксперимент для п = 100; 500; 7000; 10 000.

а) Вещественное число а образовано следующим образом. Сначала написана цифра 0, после которой поставлена запятая, а затем подряд без пробелов записаны по порядку все натуральные числа. Вот как выглядит запись этого числа, в которой приведены первые 20 цифр дробной части:

Составьте алгоритм, позволяющий определить, какая цифра записана в этом числе на п-м месте после запятой. Значение п запрашивается у пользователя.

6)* Вещественное число Ь получается аналогичным образом, но для его записи используются только чётные натуральные числа. Вот как выглядит запись числа Ь, в которой приведены первые 20 цифр его дробной части: Ь = 0,24681012141618202224.... Составьте алгоритм, позволяющий определить, какая цифра записана в этом числе на п-м месте после запятой. Значение п запрашивается у пользователя.

в)* Вещественное число с получается аналогичным образом, но для его записи используются последовательные квадраты натуральных чисел. Вот как выглядит запись числа с, в которой приведены только первые 20 цифр его дробной части: с = о, 14916253649648110012.... Составьте алгоритм, позволяющий определить, какая цифра записана в этом числе на п-м месте после запятой. Значение п запрашивается у пользователя.

г) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их. Проведите с ними вычислительный эксперимент для п = 20; 300; 7000; 10 000.

68

ф а) Перечитайте задачу 5 из 10. Составьте алгоритм, позволяющий по номеру строки определить, какая цифра стоит на п-м месте цепочки, записанной в этой строке.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм. Проведите вычислительный эксперимент для строк с номерами 7, 13, 100 и п = 100, 1000 и 10 000.

ф * Пусть а и Ь — два заданных целых числа, а х и у — пара целых чисел, удовлетворяющих уравнению ах + by = ab. Каждая такая пара (х; у) задаёт на координатной плоскости точку. Составьте алгоритм, позволяющий найти х и у, для которых соответствующая этой паре точка была бы ближайшей к началу координат. Если таких точек несколько, то нужно сообщить координаты всех таких точек.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Используя вашу программу, найдите х и у для 0=6, 10; а=о, Ь=5; а=2З, Ь=-З7•, 0=-210, Ь=-126.

Составьте алгоритм нахождения максимального значения выражения 3х² — 4у² + 2² , если натуральные числа х, у и г удовлетворяют неравенствам 4х — 5у + г < 42, х (Зу + г) < 100. б) Напишите на изучаемом вами язьке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Найдите требуемое максимальное значение.

12.2. Символьные и строковые переменные

Для хранения информации, представляющей собой один символ или последовательность символов, применяют переменные, которые соответственно имеют тип «символ» или «строка». Сокращённо эти типы мы будем записывать как сим и дщр. Последовательность символов нередко называют словом (в абстрактном смысле).

Для переменных этого типа обычно рассматриваются операции соединения (по-другому — конкатенации) и вырезки, т. е. выделения части слова.

Операция соединения состоит в том, что к первому слову приписывается второе. Команду соединения будем записывать знаком +, например:

здесь через А и В обозначены переменные строкового типа. Команду вырезки будем записывать так:

Часть  З, 5),

где на первом месте указывается сл ^ово , ^из которого вырезается часть, на втором — номер места, с которого начинается вырезаемая часть, наконец, ^{на т}ретьем месте указыва-

ется число символов в вырезаемой части. Скажем, в результате выполнения написанной команды получится слово ФОРМА. Вместо самого слова в качестве первого аргумента может указываться символьная переменная; операция тогда будет выполняться над значением этой переменной.

Команду нахождения длины слова, т. е. числа символов, из которых оно составлено, будем записывать так:

Длина

Для этой команды также вместо слова может быть указана символьная переменная, к значению которой применяется данная операция. Легко понять, что в приведённом примере результатом является число 11. Для обеих команд кавычки являются служебным знаком, показывающим, что мы имеем дело со словом, а не с именем какой-либо переменной. Поэтому кавычки не входят в число символов, участвующих в данном слове. В частности, слово может вообще не содержать символов. Такое слово называется пустым, оно обозначается как , а его длина равна О. Пустое слово надо отличать от слова , которое состоит из одного символа — пробела.

Всевозможные слова над заданным алфавитом считаются упорядоченными в алфавитном порядке. Это означает, что значения строковых переменных можно сравнивать не только на совпадение и несовпадение (равенство и соответственно неравенство слов), но и относительно заданного упорядочения, индуцированного порядком символов в алфавите.

О Какие операции применяются для действий над данными символьного и строкового типов?

При исполнении программ, использующих символьные переменные, символы считаются упорядоченными в соответствии с тем, как они располагаются в соответствующей кодовой таблице (см. Приложение, Таблицы П.1—П.4).

а) Расположите в порядке возрастания слова «?:?!»

б) Расположите в порядке возрастания слова «банк», «Саратов», «СНГ», «ЮАР», «ярмо», «Ярославль», если используется кодовая таблица СР- 1251.

в) Выполните то же задание, что и в пункте б, если используется кодовая таблица КОИ-8.

О а) Найдите слово русского языка, которое больше, чем слово ПАРА, и меньше, чем слово ПАРАБОЛА.

б) два слова называются соседними, если не существует слова, большего одного из них и меньшего другого. Являются ли соседними в русском язьке слова ПАПА и ПАПАША? Какое слово русского языка является соседним к слову ТРИБУНА?

О Рассмотрите следующий алгоритм: Алгоритм Преобразование цед: п; дт»: А;

{ Запросить п;

Повторить п

{ Если (Часть(А, 1, 1) = ” А ” или Часть(А, 1, 1) =

”Е") то

{ А := Часть(А, 2, 4) + Часть(А, 1, 1) + Часть

иначе

{ А := Часть(А, 2, 5) + Часть(А, 1,1);

Сообщить А;

Укажите наименьшее значение п, чтобы после исполнения этого алгоритма было сообщено: а) FBCEAD; б) BCEADF;

в) FBEACD.

Э * Рассмотрите следующий алгоритм: Алгоритм Преобразование+ цед: п; д-!2.• А;

{ Запросить п;

А ”ABCDEF”;

Повторить п рад

{ Если (Часть(А, 1, 1) = ”А” или Часть(А, 1, 1) — { А Часть(А, 2, 5) + Часть(А, 1, 1);

иначе

{ А:=Часть(А, 6, 1) + Часть(А, 2, 4) + Часть(А, 1, 1);

Сообщить А;

Укажите, при каких значениях п будет сообщено: а) ABCDEF;

б) FBCDAE; в) EBDCAF.

О Рассмотрите следующий алгоритм: Алгоритм Укорачивание цед: п; д-!2.• А; { Запросить А; п := Длина (А);

Делать пока (п > 1)

А := Часть(А, 2, п);

Сообщить А;

Сколько слов русского языка будет напечатано в результате исполнения алгоритма, если на запрос о значении переменной А будет введено слово: а) БОРОВ; б) ПОДВОДА; в) ПОВОРОТ?

а) Составьте алгоритм, при исполнении которого будет запрошено натуральное число от 1 до 150 — возраст пользователя — и напечатана фраза «Вам ... лет» (вместо многоточия печатается число, указанное пользователем). Фраза должна быть грамотной, т. е. для числа 22 печатается «Вам 22 года», для числа 51 печатается «Вам 51 год» и т. д.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

О а) дана строка, состоящая из нескольких слов русского языка, разделённых пробелами. Составьте алгоритм, позволяющий определить, сколько слов в этой строке.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

О а) дана строка, состоящая из нескольких слов русского языка, разделённых пробелами. Требуется сообщить слово, содержащее наибольшее количество букв (если таких слов несколько, сообщить все). Составьте соответствующий алгоритм.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

О а) Составьте алгоритмы для определения:

• является данная буква гласной, согласной или одной из букв ъ, ь; о обозначает ли данная согласная буква звонкий или глухой звук. (С овет: используйте символьные перемен ные А = ”аеиоуыэюя”, Z = ”бвгджзлмнр", G = ”кпстфхцчшщ”,

б) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их.

а) Составьте и отладьте программу для проверки правописания приставок воз- и вос- в словах русского языка. (С овет: используйте решение предыдущей задачи.)

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

а) Дана строка. Составьте алгоритм, исполнив который компьютер сообщит те символы, которые встречаются в этой строке более одного раза.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

а) Пусть имеется два слова, составленных из символов некоторого алфавита. Из них составляются новые слова так, что символы одного слова вставляются между символами другого слова с сохранением порядка следования символов в каждом из исходных слов. Например, из слов ПИЛ и АРКА можно получить слово ПАРИЛКА, а из слов ВОР и ПОТ слово ПОВТОР. Составьте алгоритм, который по трём запрашиваемым словам определяет, может ли третье слово быть получено из первых двух с помощью указанной процедуры.

б) Напишите на изучаемом вами языке программирования программы, реализующие составленный вами алгоритм, и отладьте их.

О * а) Пусть имеется строка, составленная из заглавных букв латинского алфавита. Составьте алгоритм, который удаляет наименьшее число букв, после чего остаётся строка, в которой все буквы различны и идут в алфавитном порядке. Строка запрашивается у пользователя. Например, для строки UGKFLFVOABCSTDWEZG должна получиться строка GkLOSTWZ.

б) Напишите на изучаемом вами языке программирования программы, реализующие составленный вами алгоритм, и отладьте их.

 а) Перечитайте задачу 11 из ё 10. Будем обозначать буквой У команду, по которой исполнитель умножает число на З, а буквой В команду, по которой исполнитель вычитает из числа 1. Последовательность УВ означает, что сначала число умножается на З, а затем из результата вычитается 1; запись ВУ означает, что сначала из числа вычитается 1, а затем результат умножается на З. Составьте алгоритм, который для каждого натурального числа п будет составлять последовательность команд, исполняя которую можно ПОЛУчить число п из ЧИСЛа 1 за НТIМеНЬИјее КОЛИКСТВО действий .

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм. Проведите компьютерный эксперимент для п = 100, 2000 и п = 100 000.

12.3. Переменные логического типа

Логические, или, по-другому, булевы, переменные — это переменные, принимающие только два значения. Одно из этих значений обычно обозначают Истина, другое — Ложь. Применяются также обозначения True и False,

Над логическими переменными выполняются логические операции и, иди, не, результат применения которых задаётся следующими равенствами:

Истина и Истина = Истина          Истина иди Истина = Истина

Истина и Ложь = Ложь Истина или Ложь = Истина Ложь и Истина = Ложь Ложь или Истина = Истина

Ложь и Ложь = Ложь Ложь иди Ложь = Ложь не Истина = Ложь не Ложь = Истина

В языках программирования эти операции часто обозначаются соответственно как AND, 0R и NOT.

Логические значения вырабатываются при сравнении значений переменных. Например, для числовых переменных а и Ь при сравнении а > Ь, для числовых переменных с и d при сравнении с d, для логической переменной при сравнении f = Истина. Логическое значение вырабатывается и в комбинациях операций сравнения, скажем, в такой: (х² + 7х — 15 < О) (х > 1). Указанная комбинация имеет значение Истина, например, при х = 1,5 и при х = —9, а при х = О имеет значение Ложь.

О Пусть х — переменная целого типа. Перечислите её значения, при которых истинно следующее логическое выражение:

а) (х^а +4х< 15) или (х² — 10х < 20);

б) (х^а —4х< 23) и (х^з —6х>4);

в) Часть (”потолок”, х, 1) = Часть (”потолок", 8—х, 1);

г) ((х² +7х-  и (Х<4).

дан алгоритм, вычисляющий члены последовательности, заданной правилом хп = Хп_2 — 2Хп_1 для каждого п > 2; значения Х 1 и Х2 запрашиваются у пользователя.

Алгоритм 1 лог: q; цед: К, L, М, N;

{ Запросить  значение Х1

Запросить М; (*запрашивается значение Х2*)

Если (L < О или М < О) { q := Истина; } иначе q := Ложь; }

Делать от К := 1 дд 6

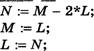
                     Если (N < О)        { q := Истина; }

Если (q = Истина) уд

{ Сообщить ”Последовательность содержит отрицательный член”} иначе

{ Сообщить ” Все члены последовательности положительны

а) Определите, каким будет результат исполнения алгоритма, если 1.

б) Определите, каким будет результат исполнения алгоритма, если = 75;

в)* Существуют ли такие Х1 и Х2, для КОТОРЫХ все шесть вычисляемых членов последовательности положительны?

г) При любых ли значениях Х1 и Ха алгоритм даёт верный ответ? Если ваш ответ «да», то его надо обосновать; если ответ «Нет», то нужно привести пример значений Х1 и Ха, для которых алгоритм даёт ошибочный ответ; укажите также, как в этом случае исправить алгоритм, чтобы получить верный ответ при любых целочисленных начальных данных.

О дан алгоритм, вычисляющий члены последовательности, заданной правилом хп  — п для каждого п > 2; значения Х1 и Х2 запрашиваются у пользователя. Алгоритм 1 лог: q; цел: К, L, М, М;

{ Сообщить ”Введите два целых положительных числа“

Запросить L; (*запрашивается значение Х1 *) Запросить М; (*запрашивается значение Х q := Истина; дедаць д.! к де 10

Если (N + L <= М или N + М <= L) то { q := Ложь }

Если (q = Истина) то

{ Сообщить “ Из отрезков, длины которых равны любым трём подряд идущим членам последовательности, можно построить треугольник иначе

{ Сообщить ”Есть три члена последовательности, которые не могут быть длинами сторон треугольника“}

Определите, каким будет результат исполнения алгоритма, если     Х2=5. А если ХЪ=5?

О Палиндромом называется слово, которое читается справа налево так же, как и слева направо.

а) Составьте алгоритм, который по введённой строке символов определит, можно ли в этой строке переставить символы так, чтобы получившаяся строка была палиндромом.

б) Напишите на изучаемом вами язьке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

Вспомогательные алгоритмы и подпрограммы

13.1. Вспомогательный алгоритм-процедура

Разновидность вспомогательных алгоритмов, называемых в языках программирования процедурами, предусматривает возможность указания прямо в самом алгоритме переменных, которым будут присваиваться результаты исполнения вспомогательного алгоритма. Вот как выглядит описание вспомогательного алгоритма данного типа:

Алгоритм Имя (аш тип: переменная, ...; тип: переменная 222 тип: переменная, . . . ) тип: переменная { действие;

Вместо простых переменных здесь могут употребляться иные структуры данных (массивы, стеки, графы и т. п.; о них см. в S 14 и 15).

Слово Алгоритм, его имя и указанные в скобках имена аргументов и результатов (вместе с их описанием) образуют заголовок вспомогательного алгоритма. Фигурирующие в заголовке алгоритма переменные называются формальными параметрами.

Обращение к вспомогательному алгоритму мы будем указывать оператором Вызвать. Записывать обращение к вспомогательному алгоритму договоримся так:

Вызвать Имя (выражение, выражение, переменная, переменная,

Выражения, стоящие на местах формальных аргументов, и переменные, указанные на местах результатов, называются фактическими параметрами. Типы выражений и переменных, являющихся фактическими параметрами, должны совпадать с типами формальных переменных, на местах которых они стоят.

Вспомогательный алгоритм для своей работы может использовать собственные (внутренние) структуры данных. Такие структуры данных называются локальными, описание их типов задаётся отдельной строкой между заголовком и телом алгоритма. Их значения не идентичны значениям одноимённых структур данных в основном алгоритме. Во вспомогательном алгоритме локальные переменные могут отсутствовать. В этом случае строка с описанием их типов тоже отсутствует.

О а) Выполнив задание 8, б из 10, вы составили алгоритм нахождения центра тяжести любого треугольника, вершины которого располагаются в вершинах клеток листа клетчатой бумаги. Используя этот алгоритм как вспомогательный, составьте алгоритм нахождения центра тяжести с помощью карандаша и линейки, пригодный для любого четырёхугольника с вершинами в вершинах клеток.

б) Нарисуйте на клетчатой бумаге какой-либо четырёхугольник, вершины которого располагаются в вершинах клеток. Предложите соседу по парте найти центр тяжести четырёхугольника с помощью составленного им алгоритма. Проверьте правильность исполнения алгоритма и правильность результата.

а)* Имеются два треугольника одинаковой площади. Составьте алгоритм, после исполнения которого один из треугольников будет разрезан на несколько таких частей, из которых можно составить другой треугольник.

б) Предложите соседу по парте нарисовать два равновеликих, но не равных треугольника и с помощью составленного вами алгоритма преобразовать один треугольник в другой. Проверьте, правильно ли был исполнен алгоритм и действительно ли из частей, на которые был разрезан первый треугольник, можно сложить второй.

в) Имеются треугольник и равновеликий ему многоугольник. Используя алгоритм, составленный при выполнении пункта б, как вспомогательный, составьте алгоритм, позволяющий разрезать треугольник на несколько частей, из которых можно составить данный многоугольник.

г) Имеются два равновеликих многоугольника. Используя алгоритм, составленный при выполнении пункта в, как вспомогательный, составьте алгоритм, позволяющий разрезать один многоугольник на несколько частей, из которых можно составить другой многоугольник.

13.2. Вспомогательный алгоритм-функция

Алгоритм-функция — это вспомогательный алгоритм, результат которого присваивается переменной не внутри этого алгоритма, а в основном алгоритме. Запись этой конструкции в нашем задачнике оформлена следующим образом.

Алгоритм Имя (тип: переменная, переменная,..,): тип тип: переменная

{ действие;

действие;

В скобках после имени перечислены формальные аргументы алгоритма-функции с указанием их типов. Вместо переменных здесь могут употребляться иные структуры данных. В конце заголовка указывается тип результата. Имя алгоритма функции одновременно служит именем локальной переменной, тип которой совпадает с типом результата.

Вызов алгоритма-функции оформляется командой присваивания:

а := Имя (переменная, переменная, ... )

Здесь переменные — это фактические параметры. Вместо переменных могут стоять выражения, допустимые для заданного типа.

( (1ВопрЪсЫиЕзЪданияй

О Рассмотрите алгоритм А, в котором использован алгоритмфункция В: Алгоритм А дед: х, у, s;

{ Запросить х;

Запросить у;

Делать пока (х + у о О)

Сообщить s;

Алгоритм В (цед: х): цел цед: К;

Делать от К = 2 до х— 2

{ Если х mod К = О то

Какое число будет сообщено, если на запросы при исполнении алгоритма А будут введены: а) х = 40, у = 36; б) х = —63, у=2О; в) х=91, у=77; г) х=-12, 12?

Ниже приведены тексты алгоритма С и алгоритмов-функций

Алгоритм С цед: К, т, п;

{ Запросить п;

Делать д.! К = п +1 до 2*п

               { Если (В (К) > т)            { т := B(h);

Сообщить т;

Алгоритм В (цел: х): цел дед: К;

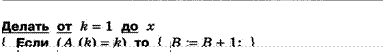
Алгоритм А (цц: х): цел цед: К;

Делать от = 1 дд х

{ А := (A*h) mod (х + 1);

Какое число будет сообщено в результате исполнения алгоритма С, если: а) п = 8; б) п = 12; в)* п = 100?

О а) Составьте алгоритм-функцию lNV (п) целого типа от целочисленного аргумента п, значением которого является число, записанное теми же цифрами, что и число п, но в обратном порядке (если на первых местах оказались нули, то их писать не следует).

б) Рассмотрите следующий алгоритм:

Алгоритм АР

             Ц.е.д:          У '  

{ Сообщить ” Введите натуральное число х”

Запросить х;

Делать пока (х о INV (х))

{ х х + INv

Сообщить х;

Исполните этот алгоритм для х = 57 и х = 86.

в) Реализуйте составленный вами алгоритм-функцию и алгоритм из пункта б на изучаемом вами языке программирования и отладьте получившиеся программы.

г)* Проведите вычислительный эксперимент для нескольких трёхзначных, четырёхзначных и пятизначных чисел. Всегда ли программа успешно завершала работу? Если нет, то укажите причину и объясните, почему произошёл сбой в работе программы. Попытайтесь устранить воздействие этой причины.

О а) Составьте алгоритм-функцию, позволяющий найти сумму четвёртых степеней цифр заданного натурального числа.

б) Используя алгоритм-функцию, составленный вами при выполнении пункта а, составьте алгоритм, позволяющий найти все числа, равные сумме четвёртых степеней своих цифр.

а) Выполнив задание 12а из пункта 12.1, вы составили алгоритм нахождения п-го простого числа. Используя этот алгоритм как основу, составьте алгоритм-функцию, аргументом которого служит натуральное число п, а результатом — простое число с номером п.

б) Вещественное число а образовано следующим образом. Сначала написана цифра О, после которой поставлена запятая, а затем подряд без пробелов записаны простые числа в порядке возрастания. Вот как выглядит запись числа а, в которой приведены первые 20 цифр его дробной части: а = 0,23571113171923293137... . Используя алгоритм-функцию, составленный вами в пункте а, составьте алгоритм, позволяющий определить, какая цифра записана в этом числе на п-м месте после запятой. Значение п запрашивается у пользователя.

в) Реализуйте составленные вами алгоритмы на изучаемом вами языке программирования и отладьте получившиеся программы. Проведите вычислительный эксперимент для п = 20; 300; 7000; 10 000.

13.3. Рекурсия

В общем случае рекурсией называется ситуация, когда какой-то алгоритм непосредственно или через другие алгоритмы вызывает себя в качестве вспомогательного. Сам алгоритм при этом называется рекурсивным.

О Рассмотрите следующий алгоритм, использующий вспомогательный алгоритм-функцию А (х):

Алгоритм цед: х;

{ Запросить х;

Сообщить х;

Алгоритм А (цел: х): цел

{ Если (х = 1)    { А := 1; } иначе

{ Если (х mod 2 = 1) то { А := З*А (х div 2) — 1; } иначе { А := 2*А (х div 2) + 1; }

Каков будет результат работы алгоритма для чисел 1; 10; 15, 100?

Алгоритм С цед: К, т, п, s•, { Запросить т;

Запросить п;

Делать д.! К = 1 дд А (т, п)

Сообщить s;

Алгоритм В (цед: х, у): цел

{ Если (х < 5) {В := х; } иначе { В := х — А (х — З, у + 1);

Алгоритм А (цед: х, у): цед

{ Если (у < х) { А := х — у; } иначе { А + В (х, у — х); }

Какое число будет сообщено, если на запросы при исполнении алгоритма С будут введены:

                 б) т = 10, п = З;                   в) т = 10, п = 10;

г) т = 10, п = О;

О* Рассмотрите ещё раз алгоритмы, представленные в задании 2. Запишите результат исполнения алгоритма С, если при исполнении этого алгоритма на его запросы будет введено значением п, равное значению т.

О Рассмотрите следующий алгоритм, использующий алгоритмфункцию Р (х):

 Алгоритм

{ Запросить х;

Сообщить х;

Алгоритм Р (цед: х): цел цед: К;

{ Если (х = 1) ц.д { Р := 2; } иначе

б— Гейн. Задачник-практикум, 10—11

Делать пока (К < х)

{ Если (Р mod Р (К) — О)

иначе

а) Какой будет результат работы алгоритма для чисел 1 ; 4; 9? 6)* Определите, для решения какой задачи предназначен данный алгоритм. Ответ обоснуйте.

Составьте рекурсивный алгоритм, подсчитывающий для запрашиваемого натурального числа п сумму кубов его цифр. Сравните его с нерекурсивным алгоритмом, который вы составили, выполнив задание 9 из пункта 14.1.

О а) Составьте алгоритм для подсчёта количества способов, которыми можно выдать сумму в п рублей монетами достоинством в 1 рубль и 2 рубля.

б) Составьте алгоритм для подсчёта количества способов, которыми можно выдать сумму в п рублей монетами достоинством в 2 рубля и 5 рублей.

в)* Составьте алгоритм для подсчёта количества способов, которыми можно выдать сумму в п рублей монетами достоинством в 1 рубль, 2 рубля и 5 рублей.

На столе стоят два столбика из чёрных и белых кубиков: в первом из них сверху п чёрных кубиков, потом п белых, а во втором столько же чёрных и белых кубиков, но они чередуются — чёрный, белый, чёрный, белый и т. д. Коля складывает из всех этих кубиков один столбик, беря по одному кубику свёрху из любого столбика наугад. Сколько различных вариантов столбика, содержащего 4n кубиков, может получиться у Коли? Составьте алгоритм, позволяющий ответить на этот вопрос.

13.4. Нисходящее и восходящее программирование

Основной метод решения сложной задачи состоит в её разбиении на более простые задачи и/или выделение в ней таких задач, решение которых уже известно. В алгоритмизации подход, связанный с разбиением на более простые задачи, называют методом нисходящего проектирования (проектированием сверху вниз); подход, при котором требующийся алгоритм собирается из готовых вспомогательных алгоритмов, называют методом восходящего проектирования (проектированием снизу вверх). Готовые вспомогательные алгоритмы, оформленные так, чтобы ими можно было легко пользоваться при конструировании других алгоритмов (нередко они оформлены как алгоритмы-функции), обычно называются стандартными и размещаются в библиотеке стандартных алгоритмов. Соответствующие подпрограммы тоже называются стандартными и размещаются в библиотеке стандартных подпрограмм.

О а) Разработайте проект решения следующей задачи с помощью компьютера, который может обрабатывать не более чем 10-разрядные целые числа.

Напечатать число п! в десятичной записи для заданного п > 30. (Через п! обозначают произведение всех натуральных чисел от 1 до п включительно.)

Реализуйте этот проект, написав соответствующие основной и вспомогательные алгоритмы. (Со в е т: обдумайте, какую структуру данных здесь целесообразно использовать для хранения цифр этого числа.)

б) На изучаемом вами языке программирования напишите программу и комплекс подпрограмм, соответствующих алгоритмам вашего проекта. Протестируйте работу вашего программного комплекса. Получите результаты для п в диапазоне от 31 до 40.

а) Пусть Р1, П, ... рп — это п первых простых чисел, занумерованных в порядке возрастания. Тогда число ... рп + 1 заведомо не делится ни на одно из чисел Р1, Ра, ... рп. При п = 1, п = 2 и п = З оно равно З, 7 и 31 соответственно, т. е. является простым числом. Всегда ли будет так, и если нет, то как часто среди чисел такой природы встречаются составные числа? Реализуйте проект, позволяющий для как можно большего п выяснить, какую долю составляют составные числа среди всех чисел такого вида. Напишите для этого соответствующие основной и вспомогательные алгоритмы. (С о в е т: воспользуйтесь решениями задач 11 и 12 из пункта 12.1. )

б) На изучаемом вами языке программирования напишите программу и комплекс подпрограмм, соответствующих алго ритмам вашего проекта. Проведите вычислительный эксперимент. для какого наибольшего п вам удалось обследовать числа указанного вида? (Результат можно признать хорошим, если вам удалось обследовать не менее 25 таких чисел.)

а) Пусть Р1, П, рп — это п первых простых чисел, занумерованных в порядке возрастания. Тогда число (Р1Р2 рп) ² + 1 тоже (как и числа, рассматривавшиеся в задании 2) не делит-

ся ни на одно из чисел Р1, П, ..., рп. При п = 1, п = 2 и п = З оно равно 2, 37 и 901 соответственно. Первые два числа простые, а третье — составное: 901 = 17 53. Реализуйте проект, позволяющий для как можно большего п выяснить, какую долю составляют составные числа среди всех чисел такого вида, написав для этого соответствующие основной и вспомогательные алгоритмы.

б) На изучаемом вами язьке программирования напишите программу и комплекс подпрограмм, соответствующих алгоритмам вашего проекта. Проведите вычислительный эксперимент. для какого наибольшего п вам удалось обследовать числа указанного вида? (Результат можно признать хорошим, если вам удалось обследовать не менее 15 таких чисел.)

 П. Ферма открыл следующую теорему: если р — простое число, то для любого натурального числа а число а ^р — а делится на р нацело. Числа, для КОТОРЫХ неверно обратное утверждение, называются числами Кармайкла. Среди первых ста миллионов имеется 255 чисел Кармайкла; наименьшее из них — 561. Разработайте проект, позволяющий находить числа Кармайкла. Проверьте, используя написанные вами программы, что число 561 действительно является наименьшим числом Кармайкла, и попытайтесь найти четыре числа Кармайкла, следующие за числом 561. (Со в е т: учтите, что число Кармайкла не является простым; обдумайте, может ли число Кармайкла быть чётным и как ограничить количество чисел а, для которых нужно проводить проверку делимости а ^р — а на р, ведь перепробовать все натуральные числа невозможно!)

Перечитайте задачу 12 из 10. Разработайте проект решения следующей задачи:

для любой пары натуральных чисел т и п составьте последовательность команд для исполнителя КВАДР, исполнив которую он за наименьшее число действий из числа т получит число п.

Реализуйте этот проект, написав соответствующие основной и вспомогательные алгоритмы.

б) На изучаемом вами языке программирования напишите программу и комплекс подпрограмм, соответствующих алгоритмам вашего проекта. Протестируйте работу вашего программного комплекса для т = 3, п = 6; т = 8, п = 28; т = 7, п = 25; т = 1, п = 16; т = 5, п = 31. Получите результаты для т = 10, п=60; т=100, п= 101.

О* Игра «Жизнь в пространстве». Эту игру на плоскости придумал Д. Конуей. Вам предлагается разработать трёхмерный аналог этой игры.

Всё пространство разбито на кубики с ребром, равным 1. В нём живут колонии закрашенных кубиков. Эти кубики рождаются и умирают (по определённым правилам), а их колонии эволюционируют во времени. Вот эти правила. У каждого кубика 6 соседних кубиков пространства, каждый из которых имеет с ним общую грань.

Правило 1. Если закрашенный кубик имеет четырёх или более закрашенных соседей, то он умирает (т. е. перестаёт быть закрашенным) от перенаселённости.

Правило 2. Если закрашенный кубик не имеет закрашенных соседей или имеет ровно одного такого соседа, то он умирает от недостатка общения.

Правило З. Если незакрашенный кубик имеет ровно трёх закрашенных соседей, то он закрашивается (в этом случае говорят, что родился новый закрашенный кубик).

Время в этой игре течёт дискретно, т. е. по шагам. За один шаг с каждым кубиком происходит (или не происходит) изменение, описанное тремя выше указанными правилами.

Пусть на поле имеется некоторая колония закрашенных кубиков. Разработайте проект, позволяющий наблюдать на экране компьютера жизнь данной колонии кубиков. Продумайте, каким цветом закрашивать кубик и как именно следует его закрасить, чтобы было удобнее наблюдать за жизнью колонии.

Проследите, как эволюционируют разные колонии из четырёх, пяти, шести, семи, восьми кубиков.

 Массивы

Массив — это набор однотипных данных, снабжённых системой из одного или нескольких индексов, каждый из

1

которых принимает последовательные целые значения . Количество используемых индексов называют размерностью массива, тип входящих в него элементов — типом данного массива.

Чтобы задать массив, надо указать его имя, тип, диапазон изменения каждого индекса. В задачнике массив будем описывать так: вещ: М [1:14, 1:25, 1:70] ² . Элемент массива также имеет имя, состоящее из имени массива и значений индексов, определяющих данный элемент.

¹ Более точно в качестве индексов может выступать любой перечисляемый тип. Поэтому, кроме целого типа, для индексирования элементов могут использоваться символьный (char) и логический (boolean) типы. Однако для простоты мы в дальнейшем в описаниях массивов будем использовать только целочисленный тип.

2

В некоторых языках программирования индекс первого элемента имеет фиксированное значение. Это необходимо иметь в виду при реализации алгоритма в виде соответствующей программы.

Каждый элемент массива фактически представляет собой отдельную переменную. Поэтому к нему можно обратиться и присвоить то или иное значение точно так же, как и для самостоятельной переменной.

Одномерный массив часто называют линейным и обычно представляют в виде строки.

Двумерный массив можно представлять себе как прямоугольную таблицу; первый индекс соответствует номеру строки, второй — номеру столбца. В таблице показано, как располагаются элементы двумерного массива А [1:3, 1:4].

	А (1,2)	А (1,3)	А ( 1,4)

В алгоритмах ввод массива М мы для краткости будем записывать одной командой:

Запросить М;

В реальных языках программирования ввод массива обычно оформляется циклом (вложенным, если массив не одномерен) в форме Делать от ... до.

О Сколько элементов содержит массив:

а) А [2:7]; б) В [-3:61; в) С [0:3, -5:0]?

О дан алгоритм, схема которого изображена на рисунке 14.1. Какое значение имеет переменная S после исполнения этого алгоритма для массива М, описанного таблицей:

-1,5

1,6

0,8

-1

1,1

1,9

о

-0,5

О Какие значения будут сообщены при исполнении следующего алгоритма для линейного массива М, заданного:

                 а) таблицей -1 2 -3 о                  1

        б) таблицей       2                      -2 1       

Алгоритм цел 1, М [1:61;

{ Запросить М [1:61; дедать

Делать от I 1 дд 6

{ Сообщить М [Л;

О Какое значение переменной К будет сообщено при исполнении следующего алгоритма для одномерного массива М, заданного: а) в задании За; б) в задании 36?

Алгоритм цед 1, к, м [1:61;

{ Запросить М [1:61;

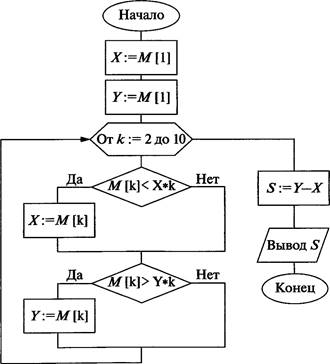
Рис. 14.1

Делать от I := 1 дд 6

{ Если (М [1] < I*I) то { К К + 1;

{ Сообщить К;

Дан двумерный числовой массив А [1:15, 1:10] целого типа. а) Составьте алгоритм для подсчёта количества чётных чисел в этом массиве.

б) Составьте алгоритм для подсчёта количества таких чисел в этом массиве, у которых первая цифра совпадает с последней.

в) Составьте алгоритм для подсчёта количества чисел в этом массиве, в записи которых нет других цифр, кроме О и 1. г) Составьте алгоритм для подсчёта количества положительных чисел в этом массиве, у КОТОРЫХ первая цифра больше второй.

д) Составьте алгоритм для подсчёта количества чисел, у которых цифры идут в порядке возрастания.

е) Составьте алгоритм для подсчёта количества пар равных между собой чисел в этом массиве.

ж) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их.

О а) дан массив А [1 :50], заполненный положительными действительными числами. Составьте алгоритм, который позволяет найти наибольшее значение среди отношений А [К]/А [т] для всевозможных пар элементов А [К] и А [т] этого массива. б) Напишите на изученном вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

Натуральное число называется составным, если оно представимо в виде произведения двух натуральных чисел, каждое из которых больше 1.

а) Составьте алгоритм, с помощью которого массив А [1 : 100] целого типа будет заполнен первыми ста составными числами. б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

О а) Составьте алгоритм, с помощью которого в заданном массиве А [1:100] целого типа будут найдены те элементы, которые являются степенями какого-либо простого числа ^[4] (не обязательно одного и того же), и сообщены их индексы или сообщено, что таких элементов нет.

б) Напишите на изучаемом вами язьке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

а) Дан массив А [1 :50] логического типа. Составьте алгоритм, при помощи которого будет сообщено значение Истина, если такое значение имеет чётное число элементов массива, и значение Ложь в противном случае.

б) Решите такую же задачу для двумерного массива в [1:15, 1:10].

дан массив А [1 :50] логического типа. Составьте алгоритм, при помощи которого будет сообщено значение Истина, если такое значение имеет больше половины элементов массива, и значение Ложь в противном случае.

б) Решите такую же задачу для двумерного массива в [1:10, 1:8].

Гусеница, сидящая на дереве, в солнечный день поднимается на 5 см вверх, если предыдущий день тоже был солнечным, а в пасмурный день спускается на З см вниз, если предыдущий день тоже был пасмурным, в остальных случаях она остаётся на месте. Если в какой-то момент гусеница доползает до вершины или до корня дерева, то она окукливается и больше ни в этот день, ни в последующие дни никуда не ползёт. дан линейный массив, содержащий 30 элементов (результаты наблюдений погоды в течение 30 последовательных дней); каждый элемент — это буква П или С в зависимости от того, пасмурным или солнечным был день. Составьте алгоритм, позволяющий по начальному местоположению гусеницы на дереве высотой 70 см определить её местонахождение и состояние по истечении 30 дней.

 дан двумерный числовой массив А [1 :25, 1 :20] вещественного типа.

а) Составьте алгоритм нахождения такого элемента этого массива, который меньше всего отличался бы от среднего арифметического значения всех элементов массива.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

             дан двумерный целочисленный массив А [1         1:n].

а) Составьте алгоритм для подсчёта количества элементов массива, меньших среднего арифметического значения всех элементов массива, и количества элементов, больших среднего арифметического значения всех элементов массива.

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её. Протестируйте вашу программу на массивах, заданных таблицами:

1	з	5		2)	-1	2	2
2	-4	6	8		5	з	7

1)

а) Из п сопротивлений собрана электрическая цепь, в которой все сопротивления соединены параллельно (рис. 14.2). Значения сопротивлений хранятся в одномерном массиве вещественного типа. Составьте алгоритм, позволяющий найти сопротивление данной цепи.

б) Составьте алгоритм, позволяющий найти сопротивление цепи, изображённой на рисунке 14.3. Значения сопротивлений хранятся в одномерном массиве вещественного типа. (Сов е т: составьте подходящее рекуррентное соотношение.)  Дан двумерный массив А [1 :25, 1:3], в котором записаны координаты 25 точек пространства. Составить алгоритм поиска двух самых удалённых друг от друга точек.

а) Дан линейный массив А [1:100] целого типа. Составьте алгоритм, позволяющий в этом массиве найти самую длинную последовательность, состоящую из подряд идущих положительных чисел.

б) Представьте, что этот массив «склеен» в кольцо, т. е. после последнего элемента снова идёт первый. Выполните задание пункта а для такого кольца.

а) Дан линейный массив А [1:100] целого типа. Последовательность элементов массива, идущих подряд в порядке возрастания индексов, называется возрастающей, если в ней каждый следующий элемент больше предыдущего. Составьте алгоритм, позволяющий в этом массиве найти самую длинную возрастающую последовательность.

б) Представьте, что этот массив «склеен» в кольцо, т. е. после последнего элемента снова идёт первый. Выполните задание пункта а для такого кольца.

Рис. 14.2

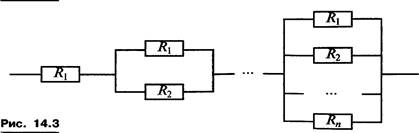
а) дан линейный массив А [1:100] целого типа. Составьте алгоритм, позволяющий в этом массиве найти самую длинную монотонную последовательность, т. е. такую, которая является либо возрастающей, либо убывающей.

б) Представьте, что этот массив «склеен» в кольцо, т. е. после последнего элемента снова идёт первый. Выполните задание пункта а для такого кольца.

Графы и алгоритмы нс графах

Граф — это совокупность точек, называемых вершинами, некоторые из которых соединены линиями. Две вершины называются смежными, если имеется соединяющая их линия, на которой нет других вершин. Если на каждой линии, соединяющей две смежные вершины, выбрано направление, то такой граф называется ориентированным или сокращённо орграфом. Линия, соединяющая две смежные вершины, для орграфа называется дугой, а для неориентированного графа — ребром.

Допускается, чтобы дуга или ребро (в данном случае безразлично) соединяли вершину саму с собой ^[5] .

Вершина называется изолированной, если она не соединена линией ни с какой другой вершиной. Вершина графа называется инцидентной данному ребру, если она является одним из концов этого ребра. В этом случае говорят также, что ребро инцидентно данной вершине.

Граф или орграф, у которого каждому ребру или соответственно каждой дуге сопоставлено некоторое число, называется нагруженным. В зависимости от рассматриваемой задачи это число может интерпретироваться как расстояние между вершинами, или как время перехода от одной вер-

2

Рис. 15.1

шины к другой, или как пропускная способность канала, соединяющего две данные вершины, или ещё каким-либо образом. Иногда бывает удобно рассматривать ненагруженный граф (орграф) как нагруженный, в котором каждому ребру (дуге) поставлено в соответствие число 1.

Обычно граф (орграф) задают одним из двух способов: перечислением всех его рёбер (дуг соответственно) или таблицей, где в клетке на пересечении строки и столбца, соответствующих данным вершинам, указано, соединены эти вершины ребром (дугой) или нет. Для нагруженного графа (орграфа) для каждого ребра (дуги) указывается нагрузка. Нагруженный орграф, изображённый на рисунке 15.1, можно задать списком дуг: (АА; 2), (АВ; З), (АС; 6), (ВС; 2), (СА; 2), (DA; 4), (DB•, 3), (DC; 5). В таблице приведена таблица смежности для этого графа.

		в
	2	з	6
в	о	о	2
	2	о	О	о
D	4	з	5

В таблице смежности ненагруженного графа везде вместо чисел, указывающих нагрузку (т. е. отличных от О), стояло бы число 1.

В заданиях к этому пункту мы для простоты будем считать вершины графа перенумерованными натуральными числами от 1 до п (без пропусков и повторений). Список дуг для нагруженного орграфа будем задавать как двумерный массив А [1:n, 1:3], где в первой строке соответствующей этому массиву таблицы указывается первый конец дуги, во второй — второй конец, а в третьей — величина нагрузки. Для неориентированного графа соответствующий массив содержит только первые две строки. Если орграф (граф) задаётся таблицей смежности, то договоримся считать значение первого индекса номером первой вершины, а второго индекса номером второй вершины; сами номера вершин в массиве не присутствуют.

О Какие вершины графа называются смежными?

О Нарисуйте какой-либо граф с девятью вершинами. Составьте для него таблицу смежности. Передайте эту таблицу смежно-

сти соседу по парте и предложите ему нарисовать граф. Проверьте, правильно ли он справился с заданием.

О Граф без изолированных вершин задан следующим списком рёбер: PQ; ps; РТ; QS; ОТ; RS.

а) Изобразите этот граф.

б) Задайте этот граф таблицей смежности.

О Нарисуйте какой-либо семивершинный граф без изолированных вершин. Запишите его списком рёбер. Передайте этот список соседу по парте и предложите ему нарисовать граф. Проверьте, правильно ли он справился с заданием.

а) Орграф, имеющий п вершин, задан списком рёбер. Составьте алгоритм, создающий по этому списку таблицу смежности.

б) Орграф, имеющий п вершин, задан таблицей смежности. Составьте алгоритм, создающий по этой таблице список рёбер.

в) Напишите на изучаемом вами язьке программирования программы, реализующие алгоритмы, составленные вами в пунктах а и б, и отладьте их.

О Дана таблица смежности графа, но неизвестно, ориентированного ли. Составьте алгоритм, позволяющий ответить, ориентирован данный граф или нет.

15.1. Свойства графов

Путь в графе (орграфе) из вершины А в вершину В это последовательность рёбер (соответственно дуг) АС1, qq, Сп 1В. Количество рёбер (дуг), составляющих путь, называется длиной этого пути. Путь, начало и конец которого совпадают, называется циклом (соответственно ориентированным циклом). Цикл длины 1 называют петлёй. Орграф, изображённый на рисунке 15.1, имеет петлю около вершины А и цикл АВСА длины З.

Граф (орграф) называется связным (соответственно сильно связным), если для любых двух различных вершин существует путь, ведущий из одной вершины в другую. Орграф на рисунке 15.1 не является сильно связным (ни из какой вершины нельзя попасть в вершину D), но соответствующий ему обычный граф является связным.

Ребро связного графа, после удаления которого он перестаёт быть связным, называется мостом. Вершина связного графа, после удаления которой он перестаёт быть связным, называется точкой сочленения.

Связный граф без циклов называется деревом.

Степенью вершины графа называется количество рёбер, инцидентных данной вершине. Если ребро является петлёй, то при подсчёте степени вершины оно учитывается дважды.

О а) Докажите, что сумма степеней всех вершин любого графа равна удвоенному числу рёбер.

б) докажите, что в любом графе количество вершин нечётной степени всегда чётно.

а) В целях борьбы с плохими дорогами правитель некоторого небольшого государства издал указ реконструировать 100 дорог, соединяющих некоторые города этого государства (каждая дорога соединяет два города, все дороги с двусторонним движением). Чтобы все города были в равном положении, мэры этих городов потребовали, чтобы из каждого города выходило ровно по 6 реконструированных дорог. Сможет ли министр транспорта и коммуникаций выполнить указ правителя с учётом требований мэров или ему лучше сразу подать в отставку? б) Позже правитель разъяснил, что в столице будет реконструировано 10 дорог, а для остальных городов пусть будет выполнено требование мэров (количество облагодетельствованных городов при этом, естественно, уменьшается). Сможет ли теперь министр выполнить указ?

в)* Чтобы избежать отставки, министр решил убедить правителя, что реконструкции 10 дорог для столицы недостаточно. Какое наименьшее число реконструируемых дорог в столице нужно назвать министру, чтобы указ стал выполнимым (конечно, это число должно быть больше 10)? Сколько при этом будет городов, где начнётся реконструкция дорог (считая и столицу)?

О В компьютерном классе 15 компьютеров. Одна фирма предложила объединить компьютеры в сеть, соединив каждый компьютер ровно с тремя другими. Сможет ли фирма выполнить своё обещание?

О Ниже приведены таблицы смежности для четырёх графов.

ппп•ппппп

•пп•ппппп ••п•пппп• •пп•ппппп шппппп•пп

п•впппппп попппппп

Продолжение

•ппппвппв

впппппппп

пп•пппппп пппппвппп

ппппппппп

а) Изобразите эти графы.

б) Укажите, какие из графов являются связными.

в) Имеется ли среди указанных графов хотя бы одно дерево?

а) для каждого связного графа, полученного вами при выполнении задания 4, выясните, можно ли построить несвязный граф с тем же набором степеней вершин.

б) для каждого несвязного графа, полученного вами при выполнении задания 4, выясните, можно ли построить связный граф с тем же набором степеней вершин

О Существует ли шестивершинный граф с заданным набором степеней вершин:

Если ответ «да», то нарисуйте подходящий граф, если ответ «Нет» — объясните почему..

для графов, изображённых на рисунке 15.2, укажите мосты и точки сочленения.

б)

н

м

О дан граф. Составьте алгоритм, позволяющий найти все его петли. Рассмотрите два варианта задания графа — списком рёбер и таблицей смежности.

15.2. Алгоритмы поиска на графе и орграфе

К стандартным задачам на графе относятся в первую очередь задачи обхода всех вершин графа и поиска пути от одной вершины к другой, обладающего тем или иным свойством.

Задача обхода всех вершин графа нередко возникает как задача полного перебора вариантов. Стандартными алгоритмами обхода являются алгоритмы поиска в глубину и поиска в ширину. В каждом случае обход начинается с некоторой вершины и, которая считается помеченной как пройденная. При поиске в глубину выбирается любая смежная с ней вершина. Она тоже считается помеченной и выступает в роли начальной вершины, т. е. разыскивается смежная с ней, но непомеченная вершина, которая снова рассматривается как начальная, и т. д. Если в некоторый момент нет вершин, которые смежны с рассматриваемой и не помечены как пройденные, то возвращаемся к предыдущей вершине и для неё выбирают очередную смежную непомеченную вершину. Процесс заканчивается, когда для исходной вершины v все смежные с ней вершины оказываются помеченными.

При поиске в ширину сначала рассматриваются все вершины, смежные с исходной вершиной v, и они помечаются как пройденные. Затем каждая из этих вершин рассматривается в роли начальной, и для неё разыскиваются все смежные с ней, но не помеченные ещё вершины, Обход заканчивается, когда нет непомеченных вершин, смежных с уже помеченными.

Оба алгоритма могут использоваться для определения того, является ли заданный граф связным (он будет таковым, если после завершения обхода не будет непомеченных вершин исходного графа.

Для поиска кратчайшего пути от одной вершины к другой в ненагруженном графе может использоваться поиск в ширину, при исполнении которого каждая вершина помечается номером шага, на котором она была достигнута. В этом случае исполнение алгоритма прекращается, как только достигнута нужная вершина. Такая модификация поиска в ширину называется волновым алгоритмом. Для нагруженных графов с положительной нагрузкой на каждом ребре для поиска пути с наименьшей суммарной нагрузкой применяют алгоритм Дейкстры. Его описание можно найти в литературе, указанной в конце задачника. Этот алгоритм применим и для орграфов.

Орграф называется бесконтурным, если в нём нет ни одного ориентированного цикла. В бесконтурном графе вершины всегда можно перенумеровать так, что начало любой дуги будет иметь номер, меньший, чем её конец. После этого поиск путей с наименьшей (или наибольшей) суммарной нагрузкой можно выполнить алгоритмом, подобным алгоритму Дейкстры. Нагрузка на дугах бесконтурного графа может быть как положительной, так и отрицательной.

О Для проведения соревнований было проложено несколько лыжных трасс; схема этих трасс с указанием протяжённости между промежуточными пунктами разветвления трасс изображена на рисунке 15.3. Старт (общий для всех трасс) обозначен буквой С, финиш (тоже общий для всех) — буквой Ф, промежуточные пункты обозначены буквами А, Б и В.

а) Для ближайшего соревнования требуется разметить трассу длиной 15 км. Укажите маршруты, удовлетворяющие этому требованию.

б) Укажите самую длинную трассу, которую здесь можно разметить, если никакой участок не предполагается проходить дважды.

в) Укажите самую короткую трассу.

Напишите на изучаемом вами язьке программирования программы, реализующие поиск в глубину для двух способов задания графа, и отладьте их.

О Напишите на изучаемом вами языке программирования программы, реализующие поиск в ширину для двух способов задания графа, и отладьте их.

О а) Составьте алгоритм, позволяющий для связного графа найти все его точки сочленения. Рассмотрите два варианта задания графа — списком рёбер и таблицей смежности.

с

                             Рис. 15.3                                    ф

7— Гейн. Задачник-практикум, 10—11

б) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы (для двух способов задания графа), и отладьте их.

а) дан нагруженный граф и две его вершины. Составьте алгоритм, позволяющий отыскать пути между этими вершинами с наименьшей суммарной нагрузкой (или сообщить, что эти вершины недостижимы друг для друга). Рассмотрите два способа задания графа и орграфа — списком рёбер и таблицей смежности.

б) Выполните такое же задание, как в пункте а для орграфа. Рассмотрите два способа задания графа и орграфа — списком рёбер и таблицей смежности.

в) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы (для двух способов задания графа или орграфа), и отладьте их.

Пусть данный граф моделирует транспортную сеть между некоторыми городами. На практике каждое ребро АВ имеет не только одну характеристику — время в пути, но ещё и стоимость проезда: путь из пункта А в пункт В занимает время t и имеет стоимость с. При этом для каждого ребра таких характеристик может быть несколько: из города в город можно добираться на машине, поезде, самолёте и т. д., а самый быстрый путь зачастую является и самым дорогим. Будем считать, что время в пути и стоимость проезда одинаковы для движения в обоих направлениях.

Граф задан списком рёбер, в котором для каждого ребра указано несколько пар чисел: первое число в паре — время в пути от одной вершины ребра до другой, второе число в паре — стоимость проезда по этому ребру.

а) Найдите самый быстрый путь в заданном графе между двумя заданными вершинами при условии, что на дорогу вы можете потратить не более S рублей. Если таких путей несколько, нужно минимизировать стоимость пути. Составьте алгоритм для нахождения таких путей. Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

б) Найдите самый дешёвый путь в заданном графе между двумя заданными вершинами, при условии что на дорогу вы можете потратить не более Т минут. Если таких наиболее дешёвых путей несколько, нужно минимизировать время пути. Составьте алгоритм для нахождения таких путей. Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

в) Выгодностью маршрута называется квадратный корень из произведения стоимости маршрута на время, затрачиваемое на движение по этому маршруту. Составьте алгоритм для нахождения самых выгодных путей в заданном графе между двумя заданными вершинами. Если таких путей несколько, то нужно минимизировать стоимость пути. Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её. (Совет: обратите внимание, что выгодность маршрута не совпадает с суммой выгодностей рёбер этого маршрута.)

а) В левом нижнем углу шахматного поля стоит конь. Составьте алгоритм, позволяющий найти кратчайший путь перемещения этого коня в другую заданную клетку шахматного поля. (Совет: подумайте, как применить здесь волновой алгоритм.) б) Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

О Имеется прямоугольное клетчатое поле размером т х п. Каждая клетка на этом поле задаётся номером ряда и номером столбца, на пересечении которых она находится. Некоторые клетки поля представляют собой ловушки; они занумерованы числами от 1 до К. Дан двумерный массив А [1 : К; 1 : 2], где А [Е; 1] — номер ряда, А [Е; 21 — номер столбца, в которых располагается клетка-ловушка с номером i. Фишка может перемещаться по этому полю, переходя из одной клетки в любую соседнюю с ней, если та не является ловушкой. Известно, что клетка, стоящая в левом нижнем углу этого поля, никогда не бывает ловушкой.

а) Составьте алгоритм, или позволяющий найти кратчайший безопасный путь (т. е. не проходящий ни через одну ловушку) из левого нижнего угла данного поля в его правый верхний, или, если такого пути нет, сообщающий об этом.

6)* Составьте алгоритм, позволяющий определить клетку, наиболее удалённую от левого нижнего угла до клетки, до которой фишка может добраться, не попав ни в одну ловушку. Расстояние между клетками — это длина отрезка, соединяющего центры клеток.

в) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их.

О Имеется прямоугольное клетчатое поле размером т х п. Каждая клетка на этом поле выкрашена одним из восьми цветов (будем считать, что цвета занумерованы числами от 1 до 8). Известно, что каждая угловая клетка поля закрашена своим цветом. Тем самым поле разбито на несколько (не менее четырёх) цветных областей — две клетки принадлежат одной цветной области, если они имеют общую сторону и закрашены одним цветом. Каждая клетка задаётся номером ряда и номером столбца, на пересечении которых она находится. дан двумерный массив А [1 : т; 1 : п], в котором А [i; ј] — номер цвета клетки, стоящей в i-M ряду и ј-м столбце.

а) Игрок первоначально владеет цветной областью, которой принадлежит клетка, стоящая в левом нижнем углу. За один ход можно поменять цвет у всех клеток своей области. При этом цветная область, принадлежащая игроку, может увеличиться за счёт присоединения «пограничных» клеток выбранного игроком цвета. Составьте алгоритм, позволяющий определить наименьшее число ходов и порядок смены цветов, позволяющих игроку овладеть всем полем.

б) Напишите на изучаемом вами язьке программирования программу, реализующую составленный вами алгоритм, и отладьте её.

в)* Пусть имеется два игрока; одному из них принадлежит клетка, стоящая в левом нижнем углу; другому — клетка, стоящая в правом верхнем. Игроки ходят по очереди, и при каждом ходе игроку запрещается для перекраски своей области выбирать цвет, которым закрашена область; принадлежащая его противнику. Игра заканчивается, когда ни один из игроков не может увеличить свои владения. Выигрывает тот игрок, которому принадлежит область из большего числа клеток.

Разработайте проект, позволяющий определить, какой игрок выигрывает при заданной начальной раскраске поля и какой должна быть его стратегия.

г)* Напишите на изучаемом вами языке программирования комплекс программ, реализующий разработанный вами проект, и отладьте их.

д)* В эту игру могут играть З или 4 игрока, если каждому выделить в первоначальное владение область с угловой клеткой. Разработайте проект, позволяющий определить, какой игрок выигрывает при заданной начальной раскраске поля и какой должна быть его стратегия. Напишите на изучаемом вами языке программирования комплекс программ, реализующий разработанный вами проект, и отладьте их.

е)* Прямоугольное поле можно заменить конфигурацией из правильных шестиугольников. Тогда в игру смогут играть 6 игроков. Разработайте проект, позволяющий описать такое поле и определять при заданной начальной раскраске поля выигрывающего игрока и его стратегию.

Игры и стратегии

Под игрой понимают процесс, в котором участвуют две или более стороны, ведущие борьбу за реализацию своих интересов. Каждый из игроков выстраивает собственный алгоритм поведения, определяемый правилами выполнения ходов игроками. Результатом игры является набор величин (по количеству игроков), называемых выигрышем соответствующего игрока. Цель игры для каждого игрока может формулироваться по-разному. В большинстве игр каждый игрок стремится добиться максимального выигрыша. Однако цель игрока может состоять и в том, чтобы обеспечить себе заранее заданную гарантированную величину выигрыша. Наконец, цель может состоять в том, чтобы минимизировать выигрыш остальных игроков. Нередко функция, описывающая выигрыш игрока, принимает только два значения, которые удобно кодировать О и 1. При этом значение 1 означает, что данный игрок выиграл, а О — что он проиграл. В случае когда возможна ничья, 1

нередко такой результат кодируют числом

Если каждый игрок в любой момент времени полностью информирован о всех предыдущих ходах, сделанных в процессе игры, и располагает информацией о всех допустимых ходах своих противников, то такая игра называется игрой с полной информацией. Игра называется конечной, если

она гарантированно заканчивается за конечное число ходов. Конечную игру с полной информацией удобно изображать в виде дерева (или орграфа) с вершинами, соединёнными дугами, — каждая вершина соответствует игровой позиции, а дуга указывает переход от одной позиции к другой при совершении допустимого хода, Около концевых вершин обычно указываются значения тех выигрышей, которые получает каждый из игроков по окончанию игры в этой позиции. Обычно значения выигрышей упорядочены по убыванию в соответствии с тем, в каком порядке игроки приходят в заключительную позицию игры или вообще не доходят до «финиша», но бывает и наоборот — выигрыш состоит в том, чтобы избежать попадания в заключительную позицию игры.

Выигрышной стратегией для данного игрока называется алгоритм, следуя которому он добьётся цели игры независимо от того, какие ходы будут совершены другими игроками.

Если в конечной игре с полной информацией участвуют только два игрока, выполняющие ходы последовательно, то все позиции могут быть разбиты на два класса — множество проигрышных позиций и множество выигрышных позиций. Если игрок, сделавший ход в заключительную позицию, считается выигравшим, то все заключительные позиции игры относятся к множеству проигрышных позиций (поскольку второй игрок из этой позиции уже сделать ход не может и автоматически является проигравшим). Если же игрок, сделавший ход в заключительную позицию, считается проигравшим, то все заключительные позиции игры относятся к множеству выигрышных позиций.

Остальные позиции распределяются между этими двумя множествами по следующему рекурсивному правилу: позиция считается проигрышной, если любой ход из этой позиции ведёт в выигрышную позицию; позиция считается выигрышной, если существует ход, ведущий в проигрышную позицию. На орграфе игры каждую вершину, соответствующую выигрышной позиции, надо отметить знаком «+» , а каждую вершину, соответствующую проигрышной позиции, надо отметить знаком «—». Если начальная позиция отмечена знаком «+» , то выигрывает игрок, делающий первый ход, и его стратегия такова: после очередного хода противника надо делать ход в ту позицию, которая отмечена знаком «—». Отметим, что при наличии такой разметки проигрышных и выигрышных позиций дуги орграфа игры для построения стратегии уже не нужны — их можно и не рисовать.

О Среди ниже перечисленных игр назовите игры с полной информацией:

а) шахматы;	б) футбол;                       в) волейбол;
г) теннис;	д) крестики-нолики;          е) домино;
ж) лото;	з) денежно-вещевая лотерея.

а) Игры, в которых игроки делают ходы строго по очереди, называются последовательными. Игры, в которых игроки могут совершать ходы одновременно, называются параллельными. Из игр, перечисленных в задании 1, укажите те, которые являются последовательными.

6)* Может ли параллельная игра быть игрой с полной информацией?

О Определите, какие из игр, перечисленных в задании 1, являются конечными, и объясните почему.

О два игрока играют в следующую игру. Перед ними лежат две кучки камней, в одной т камней, в другой п камней. За один ход разрешается увеличить число камней в любой из двух кучек на 5 или добавить в каждую из кучек по З камня. Игроки делают ходы по очереди. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в обеих кучках становится не менее 20. Постройте дерево игры, если: а) т = п = 4; б) т = 2, п = З. для каждой пары значений т и п определите, какой из игроков имеет выигрышную стратегию.

два игрока играют в следующую игру. Перед ними лежат две кучки камней, в одной т камней, в другой п камней. За один ход разрешается увеличить число камней в любой из двух кучек в З раза или добавить в каждую из кучек по 2 камня. Игроки делают ходы по очереди. Выигрывает тот, кому удастся своим ходом получить суммарное количество камней в обеих кучках, большее 20. Постройте дерево игры, если: а) т = п =4; б) т = 2, п = З. для каждой пары указанных значений т и п определите, какой из игроков имеет выигрышную стратегию.

О два игрока играют в следующую игру. Перед ними лежат три кучки камней, в первой из которых 2, во второй — З, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в какой-то кучке, или добавляет по два камня в каждую из кучек. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней во всех трёх кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока?

Из клетчатой бумаги вырезан прямоугольник размером т х п клеток, где т > 1 и п > 1, Играют двое. Игроки делают ходы по очереди. Первым ходом прямоугольник разрезается на две части по прямой, идущей по сторонам клеток. За один ход разрешается разрезать любой из имеющихся прямоугольников на две части по прямой, идущей по сторонам клеток. Выигрывает тот, кому удастся своим ходом отрезать квадратик со стороной 1. Постройте дерево игры, если: а) т = 5, п = 7; б) т = 8, п = 9. для каждой пары указанных значений т и п определите, какой из игроков имеет выигрышную стратегию.

О Рассмотрите ещё раз игру, описанную в задании 7.

а)* Докажите, что если хотя бы одно из чисел т или п больше двух и чётно, то для игрока, делающего первый ход, есть выигрышная стратегия.

б) Пусть т = 2. Исследуйте, при каких п выигрышная стратегия имеется у игрока, делающего ход первым, а при каких — у игрока, делающего ход вторым.

в)* Пусть числа т и п нечётны. Исследуйте, при каких т и п выигрышная стратегия имеется у игрока, делающего ход первым, а при каких — у игрока, делающего ход вторым.

О Игра Баше. Имеется полоска клетчатой бумаги, на крайней левой клетке которой стоит фишка. Игроки по очереди передвигают эту фишку на любое количество клеток вправо, но не более чем на клеток. Выходить за пределы полоски запрещено. Проигрывает тот игрок, который не сможет сделать очередной ход.

Рис. 16.1

а) Отметьте на полоске проигрышные позиции и определите, какой из игроков — первый или второй — выиграет, если полоска состоит из 15 клеток, а К = 4.

б) Определите, кто выиграет в этой игре, если полоска состоит из 40 клеток, а К = 6.

в) Сформулируйте правило, по которому можно узнать, кто выиграет в игре Баше, если полоска состоит из т клеток, а К — любое число, меньшее т. Высказанную вами гипотезу обоснуйте.

На рисунке 16.1 представлено поле, составленное из клеток. На клетке, отмеченной буквой Ф, стоит фишка. Игроки по очереди передвигают эту фишку на любое количество клеток вправо, верх или вниз, но не более чем на К клеток. Выполняя ход, игрок может изменять направление движения, повернув на 90⁰ (но не на 180⁰ ), но выходить за пределы поля ему запрещено. Проигрывает тот игрок, который не сможет сделать очередной ход. Если некоторая позиция повторяется трижды, то объявляется ничья.

а) Отметьте на поле проигрышные позиции и определите, имеется ли у какого-то из двух игроков — игрока, который ходит первым, или игрока, который ходит вторым, — выигрышная стратегия в этой игре при К = 4.

б) Выполните такое же задание, как в пункте а, при К = 6.

в) Нарисуйте какое-нибудь клетчатое поле и предложите соседу по парте определить, имеется ли у какого-либо из двух игроков выигрышная стратегия в этой игре для заданного вами значения К. Проверьте правильность его решения.

О* два юноши в буфете угощают девушку конфетами. За один ход можно купить 1 или 2 конфеты. Конфета стоит 1 рубль, у буфетчицы 1000 конфет, у каждого юноши по 550 рублей. Проигрывает тот, кто не может сделать очередной ход. У кого из игроков имеется выигрышная стратегия?

два игрока играют в следующую игру, делая в ней ходы по очереди. Вначале имеется число 2. За один ход разрешается имеющееся к этому ходу число увеличить на любое натуральное число, меньшее его. Выигрывает игрок, получивший своим ходом число 1000.

Два игрока играют в следующую игру, делая в ней ходы по очереди. Вначале имеется число 1000. За один ход разрешается вычесть из имеющегося к этому ходу числа натуральное число, являющееся степенью числа 2. Выигрывает игрок, получивший своим ходом число О.

Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. Ход состоит в том, что игрок перемещает фишку из точки с координатами (х; у) в одну из трёх точек: или в точку с координатами (х + З; у), или в точку с координатами (х — 1; у + 4), или в точку с координатами (х + 2; у + 2). Выигрывает игрок, после хода которого расстояние от фишки до точки с координатами (О; О) не меньше 11 единиц. Кто выиграет в этой игре — игрок, который ходит первым, или игрок, который ходит вторым, если начальная позиция фишки:

Докажите, что игра, описанная в задании 14, конечна независимо от того, какова начальная позиция фишки.

ф* Рассмотрим ещё раз игру, описанную в задании 14. Пусть игрок, выигрывающий в этой игре, получает приз, равный сумме координат той точки, в которой он оказался в момент выигрыша. Выигрывающий игрок стремится получить максимальный приз. Проигрывающий игрок стремится, чтобы величина приза у его противника была минимальна. Как он должен играть в каждой из тех позиций, которые указаны в задании 14, чтобы добиться своей цели? Какой приз при этом может гарантировать себе выигрывающий игрок?

        Основные вычислительные методы

Потребность в применении рассматриваемых здесь вычислительных методов нередко возникает при построении математических моделей и проведении вычислительного эксперимента с ними.

17.1. Методы приближённого решения уравнений

Пусть дана некоторая функция f(x) и отрезок [а; Ь], причём на концах этого отрезка функция принимает значения противоположных знаков. Если функция непрерывна, т. е. её график — непрерывная линия, то ясно, что график функции пересекает ось абсцисс в некоторой точке с отрезка [а; Ь]. Иными словами, f(c) = О, т. е. с — корень уравнения f(x) = О (рис. 17.1).

Метод Деления пополам. Чтобы найти корень уравнения f(x) = О, делим отрезок [а; Ь] пополам, т. е. берём середину отрезка (а + Ь)/2 (рис. 17.2). В этой точке вычисляем значение функции f (х). Если это значение О, то корень найден; если нет, то оно имеет тот Рис. 17.1         же знак, что и значение на одном из концов отрезка [а; Ь]. Тогда этот конец заменяем точкой (а + Ь)/2. Новый отрезок тоже содержит корень уравнения f(x) = О, поскольку на его концах функция f(x) снова имеет разные знаки, Этот отрезок в 2 раза короче предыдущего. И самое главное: с ним можно поступить точно так же. Со следуюРис. 17.2    щим отрезком ещё раз проделать то же самое и т. д. Поскольку длина отрезка

каждый раз уменьшается вдвое, можно получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x) = О. Концы отрезка дают приблиэкённое значение корня с точностью, равной длине отрезка: левый конец отрезка — приближённое значение корня с недостатком; правый конец — приближённое значение корня с избытком.

Метод хорд. Этот метод решения уравнения f(x) = О состоит в следующем. Соединим концы графика функ-

а)                                                   б)

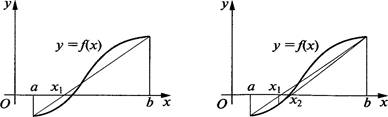
Рис. 17.3. Поиск корня методом хорд

ции f(x), который построен на отрезке [а; Ь], отрезком прямой (рис. 17.3, а). Этот отрезок пересекает ось абсцисс в некоторой точке. Возьмем её за первое приближение к корню. Затем вычисляем значение в полученной точке и снова проводим хорду; точка пересечения с осью абсцисс даёт нам следующее приближение к корню (рис. 17.3, б) и т. д.

Метод простой итерации. Для решения методом простой итерации уравнение записывают в виде х = (Р(х), после чего последовательность приближений к корню строится по формуле хп = (Р(хп 1). Гарантированное приближение этой последовательности на заданном отрезке [а; Ь] к корню обеспечивает условие (Р'(х) < 1 для всех точек интервала (а; Ь), где через (Р'(х) обозначена производная функции Уравнение f(x) = О преобразуется к виду, нужному для применения метода простой итерации, обычно следующим образом: х = х — af(x), где числовой параметр а выбирается так, чтобы выполнялось указанное ограничение на производную.

О Пусть функция на концах отрезка [1 4,5] принимает разные знаки. За сколько шагов методом деления пополам можно получить точность 0,001?

О Уравнение х^з — 5х + 3=0 на отрезке [О; 1] имеет корень (попытайтесь объяснить почему). Составьте алгоритмы нахождения этого корня:

а) методом деления пополам;

б) методом хорд;

в) методом простой итерации.

Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их. Найдите корень с точностью до 0,0001. Каким из алгоритмов это удалось сделать за меньшее число шагов? (Совет: для этого предусмотрите в программе счётчик.)

О а) Составьте алгоритмы вычисления всех корней уравнения х^з — 5х + методом деления пополам и методом хорд с точностью 0,0001. (Совет: докажите, что у этого уравнения З корня и для каждого корня найдите такой отрезок [а; Ь], на котором располагается только этот 1 корень.)

б) Напишите на изучаемом вами языке программирования программы, реализующие составленные вами алгоритмы, и отладьте их. Найдите корни с указанной точностью.

О а) для уравнения cos х = х найдите отрезок, содержащий его корень. Составьте алгоритмы вычисления этого корня с точностью 0,0001 методом деления пополам, методом хорд и методом простой итерации.

Напишите на изучаемом вами языке программирования программы, реализующие составленные алгоритмы, и отладьте их. Найдите корни с указанной точностью.

б) Выполните такое же задание, как в пункте а, для уравнения 2^х = 3х.

а) Составьте алгоритм решения системы уравнений х ² = у +2 cos ²y у ² = х +2 cos ² x

с точностью 0,0001. (Совет: докажите сначала, что для любых х и у, удовлетворяющих данной системе, выполнены неравенства —1 и —1 < у < 2.)

б) Напишите на изучаемом вами языке программирования программу, реализующую составленный алгоритм, и отладьте её. Найдите все решения системы с указанной точностью.

17.2. Датчики случайных чисел. Метод Монте-Карло

Пусть дана последовательность чисел, принадлежащих некоторому интервалу (а; Ь). Эту последовательность называют равномерно распределённой в данном интервале, если для любого интервала (х; у), содержащегося в (а; Ь), частота, с которой члены последовательности попадают в этот интервал, зависит только от длины этого интервала и не зависит от того, где на (а; Ь) этот интервал располагается. Для построения таких последовательностей используются датчики случайных чисел.

Вычислительные методы, использующие датчик случайных чисел, получили название методов Монте-Карло (по названию города, где расположена знаменитая рулетка, которую можно рассматривать как «генератор» случайных чисел). Одно из приложений метода Монте-Карло относится к приближённому вычислению площадей фигур и объёмов тел. Ниже приведено изложение указанного метода применительно к вычислению площади плоской фигуры.

Пусть дана фигура Р. Поместим её в квадрат, одна вершина которого совпадает с началом координат и две его стороны располагаются на осях координат (рис. 17.4). Пусть сторона получившегося при этом квадрата равна а. Тогда его площадь равна 0² .

Если N — общее число точек, брошенных в данный квадрат, а М — число тех точек, которые попали в фигуру F, то справедливо следующее приближённое равенство:

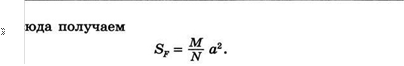
Если требуется вычислить объём пространственного тела, то оно помещается в подходящий куб.

В алгоритмах получение случайного числа из последовательности, равномерно распределённой на интервале (О; а), будем записывать командой х ДСЧ (а).

В программе обычно требуется записать оператор инициализации датчика.

Для получения случайной точки, принадлежащей квадрату со стороной а на координатной плоскости (рис. 17.4), надо дважды применить датчик случайных чисел; для получения точки, принадлежащей кубу со стороной а, датчик надо применить триэкды.          Рис. 17.4

О Рассмотрите следующий алгоритм:

Алгоритм Площадь дещ: а, х, у; цед: м, М; вещ: S;

{ Сообщить “ Введите величину стороны квадрата“ ; Запросить а;

Сообщить “ Введите количество точек, бросаемых в квадрат' ; Запросить N;

Повторить N рад

{ х а*ДСЧ (1); у а*ДСЧ (1);

                       Если (х*х + у*у < а*а) { М                 1; }

Сообщит» “ Площадь фигуры F приближённо равна“; Сообщить S;

а) Площадь какой фигуры F подсчитывается с помощью этого алгоритма?

Рис. 17.5. а) сегмент параболы; б) сегмент синусоиды; в) астроида

б) На изучаемом вами языке программирования напишите программу, соответствующую этому алгоритму, и отладьте её. Проведите вычислительный эксперимент, беря а = 2 и меняя N от 10 ООО до 1 ООО ООО с шагом 5000. Сравните полученные вами результаты со значением з, 141592653589793238462643383279502884197169399375.

в) (В Продолжите вычислительный эксперимент с тем же значением а, меняя N от 1 ООО ООО до 10 ООО ООО с шагом 100 ООО. Сравните полученные вами результаты со значением л.

О а) Составьте алгоритмы, позволяющие методом Монте-Карло найти площади фигур, изображённых на рисунках 17.5, а—в. б) На изучаемом вами языке программирования напишите программы, соответствующие вашим алгоритмам, и отладьте их.

Найдите площади указанных фигур. Сколько случайных точек оказалось достаточно «бросить», чтобы получить значение площади с точностью до 0,001?

З а м е ч а н и е: точные значения площадей этих фигур:

а) 10 3'² б) 2; в) 61.

     а)                             б)                                   в)

Рис. 17.6

а)                                   б)                                в)

Рис. 17.7. а) конус; б) параболоид; в) гиперболоид

О а) Составьте алгоритмы, позволяющие методом Монте-Карло найти площади «лунок», изображённых на рисунке 17.6, а—в. б) На изучаемом вами языке программирования напишите программы, соответствующие вашим алгоритмам, и отладьте их. Найдите площади указанных фигур. Сколько случайных точек оказалось достаточно «бросить», чтобы получить значение площади с точностью до 0,001? Замечание: точные значения площадей: а) 0,5; б) 5^п з 0,0957714003; в) 14 2.2245-2 [п 2 2,089534716.

о а) Составьте алгоритмы, позволяющие методом Монте-Карло найти объёмы тел, изображённых на рисунке 17.7, а—в.

б) На изучаемом вами языке программирования напишите программы, соответствующие вашим алгоритмам, и отладьте их. Найдите объёмы указанных тел. Сколько случайных точек оказалось достаточно «бросить», чтобы получить значение объёма с точностью до 0,001? Замечание: точные значения объёмов: а) ⁸¹ , • б) дл; в) 2х4.

о Пусть имеется вспомогательный алгоритм-функция, определяющий, лежит ли точка с координатами (х; у) внутри фигу ры F. Вот заголовок этого алгоритма:

Алгоритм Inside (аш ддщ: х, у): дщ

Если точка с координатами (х; у) лежит внутри фигуры Р, то значение функции lnside — Истина, в противном случае её значение Ложь.

Составьте алгоритм нахождения площади фигуры F методом Монте-Карло с использованием указанного алгоритмафункции.

112

 Свойства алгоритмов

Для алгоритмов рассматриваются различные их свойства. Некоторыми свойствами должны обладать все алгоритмы, необходимость других для того или иного алгоритма вытекает из постановки задачи, для решения которой предназначается данный алгоритм. Перечислим наиболее часто рассматриваемые свойства алгоритмов.

Дискретность. Под дискретностью понимается то, что алгоритм состоит из описания последовательности тактов обработки, организованной таким образом, что в начальный момент задаётся исходная ситуация, а в каждый следующий момент ситуация преобразуется на основе данных, полученных в предшествующие такты обработки. Дискретность алгоритма означает, что он исполняется по шагам: каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

Детерминированность. Это свойство означает, что на каждом шаге исполнения алгоритма (см. свойство дискретности) однозначно определено преобразование объектов среды исполнителя, полученных на предшествующих шагах алгоритма. В некоторых учебниках это свойство алгоритма называют точностью.

Результативность. Это свойство подразумевает, что каждое действие в алгоритме после своего завершения создаёт ситуацию, в которой все имеющиеся объекты однозначно определены. Если это по каким-либо причинам невозможно, то алгоритм должен сообщить, что решения задачи не существует. Это свойство является обязательным для любого алгоритма.

Нередко говорят о результативности в целом, имея в виду, что за конечное число шагов исполнения алгоритма будет получен требуемый результат или сообщено, что такой результат получить невозможно. Поэтому результативность алгоритма в целом подразумевает и его конечность, т. е. завершение исполнения алгоритма за конечное число шагов (при этом количество шагов может быть заранее неизвестным и различным для разных начальных ситуаций).

Недетерминированный алгоритм, результат исполнения которого полностью определяется начальной ситуацией, называется однозначным.

То свойство алгоритма, что в нём могут использоваться только допустимые действия исполнителя, нередко называют понятностью алгоритма (в одних учебниках — эффективностью, в других — элементарностью действий).

Понятность является обязательным свойством любого алгоритма.

Массовость. С точки зрения практической ценности алгоритма важно, чтобы множество допустимых начальных ситуаций было для него достаточно большим (иногда говорят — потенциально бесконечным).

Конечность алгоритма нужно обосновывать лишь в том случае, если в нём используется цикл, для которого заранее неизвестно количество исполнений тела цикла (т. е. цикл с предусловием или цикл с постусловием), или рекурсия. Основным инструментом обоснования конечности алгоритма в этом случае служит лимитирующая функция. Так называют переменную величину, которая каждый раз меняет своё значение при очередном исполнении тела цикла или рекурсивном обращении к вспомогательному алгоритму и обладает следующими двумя свойствами:

•        она принимает лишь конечное число значений (быть может, зависящее от исходных данных);

•        в ходе исполнения алгоритма она принимает каждое своё допустимое значение не более одного раза.

Обоснование результативности алгоритма нередко подразумевает выявление (и доказательство) того, что именно является результатом исполнения алгоритма. Одним из приёмов исследования алгоритма на результативность является обнаружение подходящего инварианта, т. е. такой характеристики объекта, обрабатываемого с помощью данного алгоритма или его фрагмента (например, тела цикла), которая не изменяется.

О Рассмотрите следующий алгоритм: Алгоритм Поиск

{ Задумайте однозначное число; Умножьте это число на 9;

Найдите сумму цифр этого произведения;

Из результата вычтите 4;

Определите букву русского алфавита, номер которой совпадает с получившимся числом;

Найдите с помощью Интернета названия всех государств, начинающихся на найденную букву;

Упорядочите найденные названия в алфавитном порядке;

В первом из названий полученного списка найдите третью букву от начала слова;

8— Гейн. Задачник-практикум, 10—11

Найдите с помощью Интернета всех млекопитающих, названия которых начинаются с найденной буквы и вес взрослой особи которых не менее 100 кг;

Если (среди найденных животных есть такие, которые живут в природных условиях найденной ранее страны) то

{ Сообщить название этого животного; } иначе { Сообщить ”Такого животного нет“; }

а) Является ли этот алгоритм детерминированным?

б) Является ли этот алгоритм однозначным?

в) Исполните этот алгоритм.

О В распоряжении учёного имеются марсианские амёбы трёх видов, каждая из которых находится в персональной пробирке. Он обнаружил, что при помещении двух амёб разного вида в одну пробирку они через некоторое время сливаются, образуя одну амёбу третьего вида. В целях исследования этого явления учёный исполняет следующий алгоритм:

Алгоритм Слияние

{ Делать пока (есть две амёбы разного типа)

{ Поместить двух разных амёб в одну пробирку;

Дождаться появления в этой пробирке новой амёбы;

а) Будет ли этот алгоритм конечным?

б) Объясните, почему этот алгоритм не является детерминированным.

в) Приведите пример таких не нулевых начальных количеств амёб и такого исполнения алгоритма, чтобы в распоряжении учёного осталась ровно одна амёба.

г) Всегда ли в результате исполнения алгоритма в руках учёного будет оставаться одна амёба?

д)* Пусть первоначально у учёного имеется 20 амёб одного вида, 21 амёба другого вида и 22 амёбы третьего вида. Может ли учёный так исполнить алгоритм, чтобы в результате осталась ровно одна амёба?

Если да, то зависит ли тип этой последней амёбы от того, как учёный выбирал амёб при исполнении тела цикла? Ответ обоснуйте.

е)* В результате исполнения алгоритма в распоряжении учёного осталась одна амёба. Зависит ли вид этой последней амёбы от того, как учёный выбирал амёб при исполнении тела цикла, или он предопределён начальной ситуацией? Ответ «да» подтвердите, приведя пример начального количества амёб разных видов, для которых при исполнении алгоритма

для разных вариантов выбора амёб, помещаемых в одну пробирку, будет оставаться одна амёба, но различного вида в зависимости от варианта выбора. Ответ «Нет» обоснуйте подходящим рассуждением.

ж)* Пусть первоначально у учёного имеется 21 амёба одного вида, 23 амёбы другого вида и 25 амёб третьего вида. Может ли учёный так исполнить алгоритм, чтобы в результате осталась ровно одна амёба? Ответ обоснуйте.

О Ниже приведены алгоритмы. Укажите, какие из них обладают свойством массовости, а какие нет. для тех алгоритмов, которые являются массовыми, постарайтесь описать множество допустимых начальных ситуаций.

а) Алгоритм Сумма дед: К, N•, ддщ: s•,

{ Запросить N;

Делать от К := 1  N — 1

Сообщить S;

б) Алгоритм Преобразование в вопрос сим: А, В;

{ А := ”Nick will до to school next year. ”,

В := Часть (А, 6, 5) + Часть (А, 1, 5) +

+ Часть (А, 11, 22) +

Сообщить В;

в) Алгоритм Значение функции

ддщ: ^х, и;

{ Запросить х;

2 COS Х — 1,7 ^х — 1,7

Сообщить у;

 Алгоритм ддщ: А, Х;

{ Запросить А;

Х := 1; (*начальное приближение*)

N := О; (*N — счётчик числа выполнений тела цикла*)

Делать пока (А — X*Xl > 0.0001)

Сообщить N;

Сообщить Х; (*N-e приближение*)

О На полке с книгами стоят п томов сочинений одного автора, расположенные, увы, не по порядку. Библиотекарь решил расположить их в порядке возрастания номеров, используя следующий алгоритм:

Делать пока (есть том, номер которого больше номера места, на котором он сейчас стоит)

{ Переставить этот том на последнее место;

а) Исполните этот алгоритм для 3—4 различных расположений четырёх томов.

б) При любом ли п будет достигнута цель, если исполнение этого алгоритма когда-нибудь закончится?

в)* Верно ли, что это исполнение этого алгоритма заканчивается за конечное число шагов при любом начальном значении п?

Рассмотрите алгоритм, обрабатывающий натуральное число п:

Алгоритм Превращение дед: п, 1;

{ Запросить п;

Делать пока (п > 1)

{ Если (п mod З * О) то { п иначе { п := п/З; }

СООбИ4ИТЬ i;

Закончится ли исполнение данного алгоритма за конечное число шагов? Ответ обоснуйте.

Рассмотрите алгоритм, обрабатывающий натуральное число п:

Алгоритм Превращение_1 дед: п, I•,

{ Запросить п;

Делать пока (п > 1)

              { Если (п mod З О)           { п

Сообщить i;

Укажите, для каких значений п, которые вводятся пользователем по запросу компьютера, исполнение данного алгоритма заканчивается за конечное число шагов. Ответ обоснуйте.

Рассмотрите алгоритм, приведённый в задании 4 из п. 13.3. Объясните, почему он будет конечным для любого натурального х.

О Элементами двумерного массива А [1 :35, 1:20] являются числа 1, —1 и О. Рассмотрите следующий алгоритм по преобразованию элементов этого массива:

Алгоритм цед: Ј, ј, К, т, А [1:35, 1:20]; лог q; { Запросить А [1:35, 1:20];

Делать пока (q = Истина) { q ложь•,

                  Делать от           1, дд 35

Делать от i 1 ДД 20

{ Если (А [i,

Если (А [i, ј] = —1) то { т := т + 1; }

( *конец цикла*)

Если (К > т) то

                      { Делать д.!         1 ДД 20

q := Истина;

Делать д.! ј := 1 дд 20

                     Делать от i 1            35

                   { Если (А [i, ј] = 1)          { К := + 1; }

Если (А [i, = —1) то { т := т + 1;

Если (К > т) то

                  { Делать д.!         1 ДД 35

 (*конец цикла*) q := Истина;

(*конец ветвления*)

(*конец цикла*)

(*конец цикла*)

Верно ли, что при любом начальном заполнении массива А алгоритм завершает свою работу за конечное число шагов? (Совет: чтобы легче было понять, как преобразуется массив, напишите программу и поэкспериментируйте с ней.)

Рассмотрите алгоритм, приведённый в задании Зг. Объясните, почему он будет конечным для любого положительного А. дан алгоритм, применяемый к натуральным значениям переменной х:

Алгоритм Особое суммирование цед: х, у, г;

{ Сообщить ”Введите натуральное число” ,

Запросить х;

Делать пока (х mod 9 у mod 9)

Сообщить х;

Через S в этом алгоритме обозначен следующий алгоритмфункция:

Алгоритм S (ар.щ ц.ед: х): цел

{ Если (х < 8) то { S := х; } иначе { S := (х mod 8) — S (х div 8); }

а) Сколько существует различных начальных значений переменной х, не превосходящих 100, для которых алгоритм «Особое суммирование» заканчивает работу за конечное число шагов? б) Сколько раз в этом алгоритме исполняется тело цикла для тех начальных значений переменной х, для которых алгоритм «Особое суммирование» заканчивает работу за конечное число шагов?

О дан фрагмент схемы алгоритма (рис. 18.1 ).

а) Закончится ли исполнение этого алгоритма за конечное число шагов, если ввести а = З и Ь = 7? А если а = 7 и Ь = З?

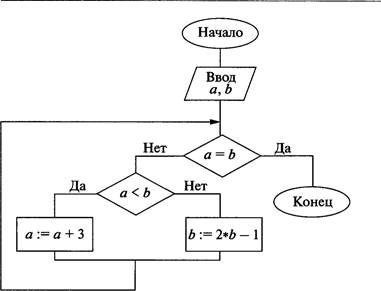
Рис. 18.1

б) Приведите пример таких неравных между собой начальных значений а и Ь, для которых исполнение этого алгоритма заканчивается за конечное число шагов.

в)* Сколько существует различных пар начальных значений переменных а и Ь, удовлетворяющих неравенствам О < а < 100,

100 и для которых этот алгоритм заканчивает работу за конечное число шагов?

Рассмотрите следующий алгоритм: Алгоритм Генератор дед: К, п, т, х; лог: q;

'

Сообщить ”Введите натуральное число п Запросить п; q := Истина;

Делать пока (q = Истина)

{ т := х*(х + 1) + п;

Делать пока (h*h <= т) щ (q = Истина)

                 { Если (т mod К = О)             q := Ложь; }

Если (q = Истина) уд { х

Сообщить х;

а) Исследуйте, для каждого ли натурального п этот алгоритм завершает работу за конечное число шагов. Ответ обоснуйте.

б) Напишите на изучаемом вами языке программирования программу, реализующую данный алгоритм, и отладьте её.

Проведите вычислительный эксперимент, задавая значения п от 1 до 50. Сколько раз и для каких п будет сообщено значение х, равное п — 2?

в)* Верно ли следующее утверждение: «Если после ввода числа п сообщено число п — 2, то число п простое»? Верно ли обратное утверждение?

Пусть N — натуральное число. Составьте алгоритм, позволяющий найти наименьшее число, записанное с использованием только цифры 1, которое делится на N, или сообщающий, что такого числа не существует.

6)* Докажите, что составленный вами алгоритм заканчивает работу за конечное число шагов, сообщив при этом правильный результат.

в)* Напишите на изучаемом вами языке программирования программу, реализующую составленный вами алгоритм. Проведите вычислительный эксперимент для N = З; 11; 17; 31.

Рассмотрите следующий алгоритм: Алгоритм Квадратичный_феномен вещ: ^а , Р, q; дед: ^м;

{ Сообщить ”Введите число р”

Запросить р;

Сообщить “ Введите число q'

Запросить q;

Делать пока (d > О)

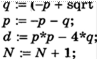           { + sqrt (d))/2;

Сообщить N;

          а) Исполните этот алгоритм для р = 6 и          5.

6)* Верно ли, что этот алгоритм завершает работу за конечное число шагов при любых начальных значениях р и q?

           Машина Тьюринга

Среда, в которой работает машина Тьюринга, представляет собой бесконечную (в обе стороны) ленту, разбитую на одинаковые секции. Во время работы машина движется вдоль ленты, смещаясь каждый раз точно на одну секцию вправо или влево. При этом машина может находиться в различных состояниях. Этих состояний конечное число, и для их обозначения мы будем использовать символы q . Набор символов, кодирующих состояния машины, называют внутренним алфавитом машины Тьюринга. Кроме того, имеется внешний алфавит, символы которого могут вписываться в секции ленты и распознаваться. Пусть это будут ао, а а . В любой момент работы машины в каждой секции хранится ровно один знак внешнего алфавита. К началу работы машины на ленту записывается исходная информация (т. е. последовательность символов внешнего алфавита). В ходе работы машины эта последовательность изменяется. Если после выполнения конечного числа действий машина прекращает работу (будем говорить — останавливается), то на ленте оказывается записанной новая последовательность символов, которую и считают результатом обработки исходной информации. Допустимые действия машины Тьюринга таковы:

•  записать какой-либо символ внешнего алфавита в секцию ленты (символ, бывший там до того, затирается);

•  сместиться в соседнюю секцию;

•  сменить состояние на одно из обозначенных символом внутреннего алфавита.

Конечно, в этом перечислении в каждой строке указано не одно действие, а группа действий одного вида — действий «записать символ внешнего алфавита» столько, сколько этих символов, сместиться в соседнюю секцию можно вправо, а можно влево, действий по изменению состояния столько, сколько этих состояний (т. е. сколько символов внутреннего алфавита). Как видно из этого описания, машина Тьюринга «бегает» вдоль ленты и заменяет одни символы на другие.

Каждая команда машины имеет вид:

указание о записи символа

указание о перемещении машины

указание о смене состояния

Фактически команды выглядят так:

— в обозреваемую секцию записать ај, сместиться вправо (к следующей секции) и перейти в состояние qj; ai 4— qj — в обозреваемую секцию записать ар сместиться влево (к следующей секции) и перейти в состояние qj; aFqj — в обозреваемую секцию записать щ, остановиться и перейти в состояние qj.

Для осуществления действий машина Тьюринга имеет операционно-логический блок. У этого блока имеется два входа: через один из них поступает информация о том, какой символ стоит в обозреваемой ячейке, через другой — символ, обозначающий состояние, в котором находится машина на данном шаге своей работы. Эта информация однозначно определяет, какую именно команду следует выполнить машине. Поскольку ко-

Рис. 19.1. Операционно-	манда может содержать указание
логический блок машины	на выполнение трёх действий —
Тьюринга	записи символа на ленту, смеще-

ния и смены состояния, операционно-логический блок имеет три выхода: запись символа А, смещение М и смена состояния Q (рис. 19.1).

Поскольку у машины Тьюринга два входа, её реакцию на подаваемые символы удобно представлять в виде прямоугольной таблицы, в которой строки и столбцы помечены символами внешнего и внутреннего алфавитов соответственно (см. таблицу). В клетки таблицы записываются команды машины. Если машина находится напротив секции, где написано ар а её состояние при этом есть q., то выполняется команда, стоящая на пересечении строки, отмеченной символом щ, и столбца, отмеченного символом qj. Если же в клетке таблицы ничего не написано, то машина прекращает работу.

Функциональная схема машины Тьюринга

Внешний алфавит А	Состояния машины Q
а

Рис. 19.2. Машина Тьюринга перед началом работы

Эту таблицу называют функциональной схемой данной машины; она-то и играет роль инструкции (программы) для машины Тьюринга.

Договоримся, что в начале работы машина всегда находится в состоянии qo и может располагаться напротив любой секции ленты. На рисунке 19.2 изображена машина Тьюринга перед началом работы при некотором заполнении ленты (слева и справа от символов «*» вся лента расписана символами «пробел», который мы никак изображать не будем). Эта договорённость означает, в частности, что «пробел» обязательно входит в число символов внешнего алфавита. Для краткости мы будем обозначать его во всех функциональных схемах как ао. Кроме того, положение машины Тьюринга мы в дальнейшем будем указывать просто Т.

О На ленте записана последовательность из п символов «*» (п — натуральное число).

а) Составьте функциональную схему машины Тьюринга, с помощью которой на ленте вместо исходной последовательности будет записана последовательность, состоящая из 2n подряд идущих звёздочек.

б) Составьте функциональную схему машины Тьюринга, с помощью которой на ленте вместо исходной последовательности будет записана последовательность из подряд 2 идущих звёздочек. (Квадратные скобки обозначают целую часть числа.)

О Пусть на информационной ленте дана следующая запись:

Её требуется преобразовать в запись:

а) Какой внешний алфавит требуется для решения этой задачи?

б) Составьте функциональную схему, следуя которой машина Тьюринга решит данную задачу. Сколько символов внутреннего алфавита пришлось вам использовать?

в) Годится ли составленная вами схема, чтобы вычислить сумму любых двух натуральных чисел. Если нет, составьте схему, которая бы решала такую задачу.

О Пусть внешний алфавит машины Тьюринга содержит символ ао, все цифры, знаки — и =. Составьте функциональную схему, следуя которой машина Тьюринга выполнит вычитание двух заданных натуральных чисел (результат может оказаться отрицательным числом).

Пусть внешний алфавит машины Тьюринга содержит символ ао, все цифры, знаки х и =. Составьте функциональную схему, следуя которой машина Тьюринга выполнит умножение натурального числа на однозначное натуральное число. Внешний алфавит состоит из символа ао и цифр О, 1, 2, 9. На ленту записано натуральное число. Составьте функциональную схему машины Тьюринга, с помощью которой на ленте будет записана сумма цифр этого числа. Ответ требуется записать правее исходного числа через пробел.

О Внешний алфавит состоит из символа ао и цифр О, 1, 2, 9. На ленту записано натуральное число в двоичной системе счисления. Составьте функциональную схему машины Тьюринга, с помощью которой на ленте будет то же число в десятичной системе счисления. Ответ требуется записать правее исходного числа через пробел.

Пусть внешний алфавит состоит из символа ао, символа «,» и цифр «0» и «1». На ленту записывается целое число в двоичной системе или конечная двоичная дробь.

а) Придумайте машину Тьюринга и составьте для неё функциональную схему, согласно которой данное число будет увеличено вдвое. Если после удвоения получается целое число, то в его записи не должно быть символа «,». Например, запись на информационной ленте

должна быть преобразована в запись

а запись

должна быть преобразована в запись

б) Придумайте машину Тьюринга и составьте для неё функциональную схему, согласно которой данное число будет уменьшено вдвое. Если после этого снова получается целое число, то в его записи не должно быть символа «,».

Пусть внешний алфавит машины Тьюринга содержит символ ао и все гласные буквы русского алфавита.

а) Составьте функциональную схему, следуя которой машина Тьюринга расположит в алфавитном порядке заданную на информационной ленте последовательность гласных букв (последовательность не содержит одинаковых букв). Например, запись на информационной ленте

должна быть преобразована в запись

Совет: в условии не требуется, чтобы результат располагался в точности на тех же местах, где стояла исходная последовательность; подумайте, как этим можно воспользоваться для облегчения решения задачи.

б) Выполните такое же задание, как в пункте а, но допуская теперь, что буквы в последовательности могут повторяться.

Языки программирования

В этом параграфе представлено несколько заданий, которые предназначены для начального освоения языка (в том числе, его синтаксиса) и некоторых приёмов программирования. Поэтому все задания выполняются без компьютера. По тем же причинам в этом параграфе нет заданий на разработку программ (тем более что таковые в достаточном, на наш взгляд, количестве и ассортименте присутствуют в других параграфах этой главы).

Все программы приводятся на трёх языках: Бейсик, Паскаль и Си. Внутри одного задания эти программы идентичны — при выполнении задания нужно только выбрать ту, которая записана на изучаемом вами языке.

О дан фрагмент программы, в которой переменные а и Ь имеют вещественный тип:

Бейсик	Паскаль	Си

Какое значение получит переменная Ь после исполнения этого фрагмента?

О дан фрагмент программы, в которой переменные а, Ь и К имеют целый тип:

	FORk=1 T04 (Ф > К) OR (а < i)) THEN а ELSE Ь = а + К NEXT К PRINT а, Ь	К
	for К := 1 to 4 do if (Ь > К) or (а < К) then а := Ь — К else Ь := а + К; writeln (а); writeln (Ь);
	for (К = 1; К <= 4; Кн) if (Ь > К) or (а < К) then а := Ь — К; else Ь := а + К; printf(a); printf(b);

Какое значение получат переменные а и Ь после исполнения этого фрагмента?

О В программе описан одномерный целочисленный массив А с индексами от О до 10, i и s — переменные целого типа. Ниже представлен фрагмент этой программы:

Бейсик	Паскаль	Си
FOR i = О ТО 10 NEXT i FOR i = О ТО 10 А (i) = А (10 NEXT i FOR i = О ТО 10 NEXT i	for i := О to 10 do for i := О to 10 do А [10 - i]; for i := О to 10 do	for (i = О; i             10; for (i = О; i             10; i++) А [i] = А [10 - i]; for (i = О; i             10; i++) s = s + А [il;

Какое значение получит переменная s после исполнения этого фрагмента?

О В программе описан одномерный целочисленный массив А с индексами от О до 10, i и s — переменные целого типа. Ниже представлен фрагмент этой программы:

Бейсик	Паскаль	Си
FOR i = О ТО 10 NEXT i FOR i = 9 ТО О STEP - 1 NEXT i FOR i = О ТО 10 NEXT i	for i := О to 10 do :=i— 1; for i := 9 downto О do for i := О to 10 do	for (i = О; i <= 10; i++) for (i = 9; for (i = О;

Какое значение получит переменная s после исполнения этого фрагмента?

О В программе описан двумерный целочисленный массив А, оба индекса которого меняются от О до 7, и ј — переменные целого типа. Ниже представлен фрагмент этой программы, в котором заполняется массив:

Бейсик
FORi=OT07 FORj=OT07 NEXT Ј NEXT i	for i О to 7 do for ј О to 7 do begin А [ј, il :=i; end;	for (i = О; i 7; i++) for (ј = О; ј е 10; ј++)

Какое число в этом массиве встречается наибольшее число раз?

О Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки заштрихованной области, включая её границы (рис. 20.1). Программист то-

У —2	у—х=2 х2+у2=4 2
	х

ропился и запрограммировал неверный алгоритм.

1)           Приведите пример таких чисел х, у, при которых программа неверно решает поставленную задачу.

2)           доработайте эту программу так, чтобы не было случаев её неправильной работы. (Такая доработка подразумевает включение в программу ещё нескольких операторов, позволяющих устранить

Рис. 20.1                                      ошибки алгоритмизации.)

INPUT х, У IF        +             4 THEN IF у -2 THEN IF у - х с: 2 THEN PRINT “ принадлежит" ELSE PRINT “ не принадлежит“ ENDIF

Продолжение

	ENDIF ENDIF END
	var х, у: real; begin readln (х, у); if х*х + у*у >= 4 then if у >= —2 then if у — х 2 then write ('принадлежит') else write ('не принадлежит') end.
	void main(void) { float х, у; scanf ( “ % f % f” if (х*х + у*у >= 4) if (у —2) if (у — х <= 2) printf (”принадлежит”); else printf (”не принадлежит");

9— Гейн. Задачник-практикум, 10—11

вычислительной техники

В компьютере вся информация представляется в двоичном коде. Это положение называют принципом двоичного кодирования — одним из трёх так называемых принципов фон Неймана, лежащих в основе вычислительной техники. Соответственно обработка информации в компьютере — это преобразование исходной последовательности над двухсимвольным алфавитом в результирующую последовательность. Символы алфавита договоримся обозначать «О» и «1». Технически двухсимвольный алфавит может быть реализован по-разному: низкий и высокий потенциал напряжения, отсутствие или наличие намагниченности, низкая или высокая интенсивность светового потока. Для осуществления такого двоичного кодирования напряжение на все логические элементы компьютера подаётся дискретно — импульсами — с определённой тактовой частотой. Появление импульса на входе логического элемента кодирует подачу символа «1» на этот вход. Отсутствие импульса на входе кодирует подачу символа «О» .

Средством для математического описания работы логических элементов является язык математической логики. Поэтому параграфы, посвящённые различным аспектам основ вычислительной техники, предваряются параграфами, относящимися к математической логике. В них вместо 1 и О используются традиционные для математической логики символы И и Л. Первый из них означает истинность высказывания, второй — его ложность. Элементы математической логики представляют самостоятельный интерес, а многие предлагаемые задания близки к тем, которые применяются в ЕГЭ по информатике.

 Элементы математической логики

Одну из простейших моделей рассуждения представляет математическая логика, основным понятием которой является «высказывание». Над высказываниями можно выполнять операции, о которых кратко рассказывается в п. 21.1.

21.1. Алгебра логики

Высказывание — повествовательное предложение, о котором можно сказать, истинно оно или ложно. Договоримся высказывания обозначать большими латинскими буквами.

Если А и В — некоторые высказывания, то высказывание «А и В» называется конъюнкцией указанных высказываний и обозначается А л В, высказывание «А или В» называется дизъюнкцией указанных высказываний и обозначается А v В, высказывание «не А» называется отрицанием высказывания А и обозначается „А, высказывание «если А, то В» называется импликацией высказываний А и В и обозначается А В, высказывание «А тогда и только тогда, когда В» называется эквивалентностью и обозначается А е» В. Символы л, м,  называются логическими связками.

Зависимость значений истинности полученных с помощью связок высказываний от значений истинности высказываний А и В определяется таблицей истинности связок.

Таблица истинности связок

	в	Ал В	AvB
и	и	и	и	л	и	и
и	л	л	и	л	л	л
л	и	л	и	и	и	л
л	л	л	л	и	и	и

Если Щ, А Ап — обозначения некоторых высказываний, то выражение, полученное из них с помощью связок, называется формулой. В формуле могут использоваться скобки для указания порядка применения связок. Чтобы писать меньше скобок, договариваются, что связка -, старше связки л, а связка л старше связки м, которые, в свою очередь, старше связок и Если символам придавать значение И или Л, то с помощью таблиц истинности для связок можно вычислить соответствующее значение форму-

лы. Формула называется тождественно истинной, если при любых значениях входящих в неё символов она принимает значение И. Две формулы от одного и того же набора символов называются равносильными, если у них одинаковые таблицы истинности. Равносильность формул будем обозначатЬ

О Из приведённых ниже предложений выберите высказывания и обоснуйте свой выбор:

а) «В тот год осенняя погода стояла долго на дворе» (А. Пушкин);

б) «Никто не может объять необъятное» (К. Прутков);

в) «Давайте восклицать, друг другом восхищаться» (Б. Окуджава);

г) «Не жалею, не зову, не плачу» (С. Есенин);

д) «Если у вас нет собаки, её не отравит сосед» (А. Аронов);

е) «Пусть всегда будет солнце!» (Л. Ошанин);

ж) «Я спросил у ясеня: «Где моя любимая?» (В. Киршон)

з) «Скажи-ка, дядя, ведь недаром Москва, спалённая пожаром, французу отдана?» (М. Лермонтов)

и) «Никого не будет в доме, кроме сумерек» (Б. Пастернак);

к) «А где мне взять такую песню и о любви, и о судьбе?» (М. Агашина);

л) «Пусть бегут неуклюже пешеходы по лужам, а вода — по асфальту рекой» (А. Тимофеевский).

Составьте таблицы истинности для следующих формул:

О Проверьте равносильность формул:

О а) Известно, что высказывание

истинно. Какое наименьшее число ложных высказываний может быть среди высказываний А, В и С?

б) Известно, что высказывание

ложно. Какое наименьшее число истинных высказываний может быть среди высказываний А, В и С?

а) Укажите, какие из высказываний А, В и С истинны, а какие ложны, если составленное из них высказывание

ложно.

б) Выполните задание а, если для высказываний А, В и С истинно высказывание

О* а) Укажите, какие из высказываний А, В, С и D истинны, а какие ложны, если известно, что истинно высказывание

а высказывание

ложно.

б) Выполните задание а, если для высказываний А, В, С и D истинны высказывания ((D v С) —В) л (D v В)

Постройте формулу F, имеющую таблицу истинности:

х

а)

х

б)

Продолжение

и	и	и	и	и
и	и	и	л	л
и	и	л	и	и
и	и	л	л	л
и	л	и	и	л
и	л	и	л	и
и	л	л	и	л
и	л	л	л	и
л	и	и	и	и
л	и	и	л	и
л	и	л	и	и
л	и	л	л	л
л	л	и	и	л
л	л	и	л	и
л	л	л	и	л
л	л	л	л	и

О Последовательность высказьваний Ап определена следующим образом:

Ап = (Ап _1 Л Ап _2) V (Ап_з

Известно, что А1 — истинно, А2 — ложно, Аз — истинно. Какое значение имеет А2000?

 Определите, существует ли формула Е, такая, что ей тождественно истинна формула G:

1.2. Высказывательные формы (предикатьи)

Высказывательная форма (предикат) — утверждение, содержащее одну переменную или более и становящееся высказыванием, когда переменным приданы конкретные значения. Предикаты, как и высказывания, можно соединять логическими связками. Предикаты мы будем обозначать большими латинскими буквами, а фигурирующие в них переменные — малыми латинскими буквами (с индексами или без них).

Над предикатом может выполняться операция связывания переменной. Если Р (х х х ) — предикат, зависящий от переменных % , х хп, то утверждение «для любого х1 Р (х х х )» является предикатом от переменных х х . Такой способ получения нового предиката называется связыванием переменной х1 квантором всеобщности. Аналогично о предикате «существует х1 х )» говорят, что он получен из предиката х ) связыванием переменной х1 квантором существования. В частности, если исходный предикат зависел только от одной переменной, то после её связывания получается высказывание. Переменные, не связанные никаким квантором, называются свободными.

Для обозначения кванторов применяют символы «М» (квантор всеобщности) и «З» (квантор существования).

О Среди приведённых ниже предложений укажите те, которые являются предикатами. для каждого из этих предикатов назовите свободные переменные, которые он имеет.

а) Окружность вписана в треугольник.

б) Ученик пришёл в школу.

в) Кому на Руси жить хорошо?

г) Книга будет напечатана в этом году.

д) Впишите треугольник в окружность.

е) Проект завершён.

ж) Число О делится на любое число.

з) Верно ли, что число делится на 5?

и) для каждого натурального числа есть натуральное число, большее его.

к) Младшие уважают старших.

л) Переходить перекрёсток нужно только на зелёный свет светофора.

м) Не каждый ответит на вопрос: «Кому на Руси жить хорошо?»

для каждого из приведённых ниже предикатов укажите свободные и связанные переменные, называя тип связывающего квантора:

        а) Мх Ву (х + у = г л           v (xz <

б) Ух (х + у = г v Зу (xz < у));

в) Мх (Вг (х + О) v Ву (xz <

О Пусть область допустимых значений переменных х, у и г — множество целых чисел. Вьнислите значение предиката мх (Зу (х + у = г л г > О) v (хг лу < О)):

          а) при у = 1 и 2= 1;              б) при у = 1 и г—

          в) при у =—1 и 2=2;           г) при у =—1 и 2=—1.

О Пусть область допустимых значений переменных х, у и г — множество целых чисел. Найдите все значения переменной г, для которых предикат Ух Зу (х + у = г л хг > у)) принимает значение Истина.

 Рассмотрим предикат D (х, у): «число х делится нацело на ч исло

а) Пусть этот предикат рассматривается на множестве всех натуральных чисел (т. е. всех целых положительных чисел). Запишите каждое из высказьваний Ух Му (D (х, у)); Ух Ву (D (х, у)); ах Му (D (х, у)); 3х Ву (D (х, у)) предложением русского языка. Определите, какие из этих высказываний истинны, а какие ложны.

б) Выполните задание пункта а, если предикат D (х, у) рассматривается на множестве всех целых чисел.

в) Выполните задание пункта а, если предикат D (х, у) рассматривается на множестве всех положительных рациональных чисел.

О Пусть Р (х, у, г) — предикат от трёх переменных х, у, г, означающий, что точка у лежит между точками х и г. Существует восемь вариантов связывания переменных х., у, z (в указанном порядке) кванторами всеобщности и существования. Вот три из этих вариантов: ах Му Мг Р (х, у, г); Ух Ву Vz Р (х, у, г); Ух Му 3z Р (х, у, г).

а) для приведённых вьше вариантов укажите, какие из них являются истинными высказьваниями.

б) Запишите остальные пять возможных вариантов связьвания переменных и для каждого из них определите, истинное или ложное высказьвание получается.

в) Если порядок связьвания переменных изменять, то можно получить ещё 40 записанных по-разному высказьваний. Вот пять из них: Зу мх Vz Р (х, у, г); Ух Згну Р (х, у, г); Ву мх Р (х, у, г); ВуВх Vz Р (х, у, г); Му Ех Р (х, у, 2). Укажите, какие из этих высказьваний истинны.

О Пусть Р (х, у) — произвольный предикат от свободных переменных х и у. Верно ли, что для любого предиката Р (х, у) следующие два высказьвания одновременно истинны или одновременно ложны:

в) 3х Му Р (х, у) и Му 3х Р (х, у)?

О Рассмотрите предикаты, заданные на множестве натуральных чисел:

а) «х — нечётное число, и для любого нечётного числа у выполнено неравенство х < у»; б) «х — простое число, и для любого простого числа у выполнено неравенство х < у».

дпя каждого из этих предикатов укажите все те значения аргумента х, для которого данный предикат истинен.

О На множестве натуральных чисел рассматривается предикат 3х Уу (у > zx² — 3х). Укажите все значения переменной г, для которых данный предикат истинен.

На множестве целых неотрицательных чисел задан предикат S (х, у, г) — число равно сумме чисел х и у. Используя этот предикат, запишите подходящей формулой каждое из следующих утверждений:

         а) число х равно О;                          б) число х чётно;

в) число х не больше числа у; г) числа х и у равны;

          д) число х равно 1;                           е) число х кратно З.

О На множестве натуральных чисел задан предикат S (х, у, г) — число г равно сумме чисел х и у. Используя этот предикат, запишите подходящей формулой каждое из следующих утверждений:

         а) число х чётно;                              б) число х кратно З;

          в) число х меньше числа у;              г) числа х и у равны;

          д) число х равно 1;                            е) число у равно 2х+ 1.

На множестве натуральных чисел задан предикат S (х, у, г) — число равно сумме чисел х и у. Используя этот предикат, запишем формулу, содержащую некоторый предикат Р (х, у):

Р (х, у) (Ми Vw S (и, w, х)) & (Ми Vw — S (и, w, у)) v v (Ви Bw (S (w, 1, х) л Р (ш, и) A S (х, и, у))).

Будем считать, что эта формула тождественно истинна.

а) Найдите значения Р (1, 1); Р (2, 2); Р (2, З); Р (4, 3); Р (5, 15).

б) Пусть х = З. Укажите те значения переменной у, для которых предикат Р (х, у) имеет значение Истина. в) Пусть у = 15. Укажите те значения переменной х, для которых предикат Р (х, у) имеет значение Истина.

г) Пусть у = 13. Найдётся ли такое значение переменной х, для которого предикат Р (х, у) имеет значение Истина?

д)* Докажите, что значение Р (х, у) действительно однозначно определено при любых заданных значениях переменных е)* Докажите, что предикат Р (х, у) имеет значение Истина тогда и только тогда, когда у =

На множестве натуральнь•х чисел задан предикат S (х, у, г) — число г равно сумме чисел х и у. Выполнив задание 11, вы с помощью этого предиката записали предикаты «число х равно 1» и «число у равно 2х + 1». Обозначим эти предикаты для краткости как Опе (х) и L (х, у) соответственно. Используя эти предикаты, запишем формулу, содержащую некоторый предикат Р (х, у):

Р (х, у) еэ (Опе (х) л Опе (у)) v (Ви Ви; (S (ш, 1, х) л

Будем считать, что эта формула тождественно истинна.

а) Найдите значения Р (1, 1); Р (2, 4); Р (З, 6); Р (4, 2); Р (5, 25).

б) Пусть х = З. Укажите те значения переменной у, для которых предикат Р (х, у) имеет значение Истина. в) Пусть у = 16. Укажите те значения переменной х, для которых предикат Р (х, у) имеет значение Истина.

г) Пусть у = 13. Найдётся ли такое значение переменной х, для которого предикат Р (х, у) имеет значение Истина?

д)* Докажите, что значение Р (х, у) действительно однозначно определено при любых заданных значениях переменных

е)* Докажите, что предикат Р (х, у), имеет значение Истина тогда и только тогда, когда у = х²

На множестве  чисел задан предикат S (х, у, г) — число z равно сумме чисел х и у. Выполнив задание 11, вы с помощью этого предиката записали предикат «числа х и у равны». для краткости обозначим его через R (х, у). Используя предикаты S и R, запишем формулу, содержащую некоторый предикат U (х, у, г):

Будем считать, что эта формула тождественно истинна.

а) Найдите значения U (1, 1, 1); U (2, 2, 2); U (2, З, 6).

б) Пусть х = З, у = 5. Укажите те значения переменной 2, для которых предикат U (х, у, г) имеет значение Истина.

в) Пусть х = 5, г = 30. Укажите те значения переменной у, для которых предикат U (х, у, г) имеет значение Истина. г)* Докажите, что значение U (х, у, г) однозначно определено при любых заданных значениях переменных х, у и г.

д)* Докажите, что предикат U (х, у, г) имеет значение Истина тогда и только тогда, когда z = ху.

на множестве натуральных чисел задан предикат S (х, у, г) — число z равно сумме чисел х и у. Выполнив задание 11, вы с помощью этого предиката записали предикат «числа х и у равны». Обозначим этот предикат для краткости как R (х, у). Используя предикаты S (х, у, г) и

139

R (х, у), запишем формулу, содержащую некоторый предикат

Р (х, у, г) (R (х, у)             (х, г)) v (Ви (S (г, и, х) л л Р (и, у,   v (Ви (S (х, и, у) л

Будем считать, что эта формула тождественно истинна.

а) Найдите значения Р (З, З, З); Р (5, 2, 6); Р (4, 4, 8);

б) Пусть х = 18, у = 12. Укажите те значения переменной г, для которых предикат Р (х, у, г) имеет значение Истина. в) Пусть х = 15, г = 5. Укажите все значения переменной у, для которых предикат Р (х, у, г) имеет значение Истина.

г)* Докажите, что значение Р (х, у, г) однозначно определено при любых заданных значениях переменных х, у и г.

д)* докажите, что при любых заданных значениях переменных х и у существует, и притом единственное, значение переменной г, для которого предикат Р (х, у, г) имеет значение Истина.

На множестве натуральных чисел задан предикат S (х, у, г) — число z равно сумме чисел х и у. Выполнив задание 11, вы с помощью этого предиката записали предикат «числа х и у равны». Обозначим этот предикат для краткости как R (х, у). Используя эти предикаты, запишем формулу, содержащую некоторый предикат Р (х, у):

Будем считать, что эта формула тождественно истинна.

а) Найдите значения предиката Р при х = у = 2; при х = у = З; при х = З и у = 5;

б) Пусть х = 4. Укажите те значения переменной у, для которых предикат Р (х, у) имеет значение Истина. в) Пусть у = 13. Укажите те значения переменной х, для которых предикат Р (х, у) имеет значение Истина.

г) Пусть у = 15. Найдётся ли такое значение переменной х, для которого предикат Р (х, у) имеет значение Истина?

д)* Докажите, что значение Р (х, у) действительно однозначно определено при любых заданных значениях  х

е)* Докажите, что при любом заданном значении переменной х существует, и притом единственное, значение переменной у, для которого предикат Р (х, у) имеет значение Истина.

 Релейно-контсктные схемы

Релейно-контактная схема — это электрическая схема, содержащая один или несколько переключателей, позволяющих управлять прохождением тока через эту схему. Два переключателя можно соединить либо последовательно (рис. 22.1, а), либо параллельно (рис. 22.1, б).

                     а)                              б)

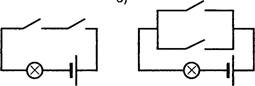
Рис. 22.1

Для математического описания релейно-контактных схем и изучения их свойств используются методы математической логики. Каждый переключатель обозначается как переменная, принимающая значение О (Ложь) или 1 (Истина), параллельное соединение двух переключателей соответствует операции ИЛИ, обозначаемой символом ч, последовательное соединение — операции И, обозначаемой символом л. Один и тот же переключатель может фигурировать в разных частях электронной схемы, в этом случае он обозначается одной и той же буквой. Если некий контакт разомкнут тогда и только тогда, когда контакт Х замкнут, то такой контакт обозначается как —Х. Тем самым каждой схеме можно сопоставить логическое выражение, которое принимает значение 1 при заданных значениях переменных тогда и только тогда, когда при соответствующем положении переключателей через эту схему идёт электрический ток. Верно и обратное утверждение: по логическому выражению можно построить последовательно-параллельную схему, для которой выполнено указанное свойство.

звопросытиузадсният,:

О Почему в электронной вычислительной технике обычно используется двухсимвольное кодирование?

О для каждой из схем, изображённых на рисунке 22.2, запишите соответствующее ей логическое выражение.

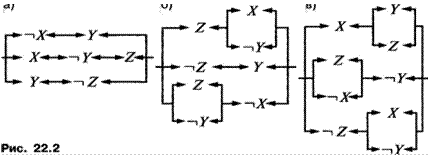
О Для каждого из приведённых ниже логических выражений нарисуйте соответствующую ему последовательно-параллельную схему:

                  л У);

О Напишите какое-либо логическое выражение, содержащее три переменные, и предложите соседу по парте нарисовать соответствующую этому выражению последовательно-параллельную схему. Проверьте, правильно ли он выполнил задание. для схем, изображённых на рисунке 22.3, постройте эквивалентные им более простые схемы.

О для каждой мостовой схемы, изображённой на рисунке 22.4, построить эквивалентную ей последовательно-параллельную схему.

а) Известно, что высказывание F, зависящее от трёх вы-

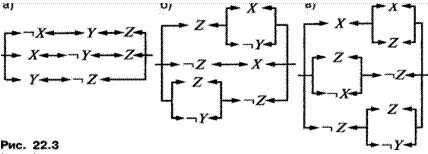
142

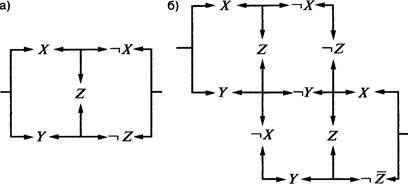
Рис. 22.4

сказываний А, В и С, принимает то значение для каждого данного набора значений А, В и С, которое принимает большинство из этих трёх высказываний. Функцию F поэтому называют функцией голосования. Составьте для F логическую формулу.

б) Составьте релейно-контактную схему, реализующую функцию голосования для трёх участников.

        Логические элементы. Вентили

Логическим элементом или вентилем называют устройство с п входами и одним выходом, которое преобразует входные двоично закодированные сигналы в двоичный сигнал на выходе. Каждый вентиль является, по существу, некоторой релейно-контактной схемой; входы вентиля — это электронно управляемые переключатели такой схемы.

Условно логический элемент f можно изобразить так, как показано у на рисунке 23.1. Поскольку внутреннее устройство вентиля нас не интересует, можно рассматривать его как некоторый чёрный ящик.

Различных логических элементов Рис. 23.1 с п входами существует 2 ^{2 п} В таблице указано, как обрабатывает входной сигнал каждый из четырёх логических элементов с одним входом.

Логические элементы с одним входом

Входной сигнал х	Сигнал на выходе

Первый из этих элементов называется тождественной единицей, второй — просто тождественным, третии — отрицанием, или вентилем НЕ, четвёртый — тождественным нулём.

В таблице указано, как обрабатывает пару входных сигналов каждый из 16 логических элементов с двумя входами.

Логические элементы с двумя входами

Входной сигнал ХIХ2	Сигнал на выходе
оо
01
10
11
Входной сигнал	Сигнал на выходе
оо
01
10
11

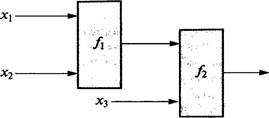
Рис. 23.2. Комбинация f2(f1 (хр х», хз) элементов f1 и f2

Приведём общепринятые названия некоторых из этих логических элементов (не повторяя тех, которые названы ранее).

Элемент & называется конъюнкцией. Другое название для него — вентиль И.

Элемент v называется дизъюнкцией. Другое название для него — вентиль ИЛИ.

Элемент называется импликацией.

Элемент — называется эквиваленцией.

Элемент О называется сложением по модулю 2. Элемент называется операцией Шеффера.

Элемент называется операцией Пирса.

Логические элементы можно комбинировать друг с дру-

в)

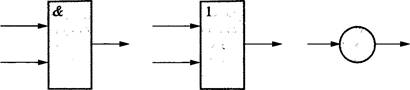
Рис. 23.3. Обозначения вентилей И, ИЛИ, НЕ

       а)                  б)                   в)                    г)                   д)

1   1

Рис. 23.4. Стандартные изображения вентилей: а) эквиваленция; б) сравнение по модулю 2; в) импликация; г) операция Пирса; д) операция ШефФера

гом, подавая на входы одного элемента то, что получилось на выходах других элементов. Пример такой комбинации приведён на рисунке 23.2.

Получившееся устройство естественно рассматривать как логический элемент с тремя входами % , 4, х .

Оказывается, что, комбинируя вентили НЕ, Й, ИЛИ, можно собрать схему, равносильную любому логическому элементу от любого числа переменных. Для удобства эти вентили в схемах обозначают так, как показано на рисунке 23.3. Обозначения других наиболее употребительных вентилей с двумя входами приведены на рисунке 23.4.

О а) Составьте формулу, описывающую схему, изображённую на рисунке 23.5.

б) Составьте таблицу значений логической функции, реализованной схемой, изображённой на рисунке 23.5.

в) Какая функция из перечисленных в таблице на с. 144 эквивалентна логической функции, реализованной данной схемой?

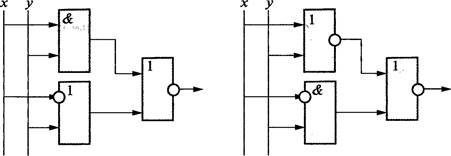
Рис. 23.5                                               Рис. 23.6

Рис. 23.7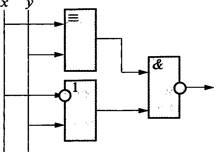                     

1 О— Гейн. Задачник-практикум, 10—11

ху Z

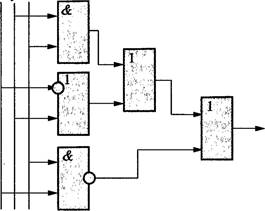
Рис. 23.8

О Выполните задание 1 для схемы, изображённой на рисунке 23.6.

О Выполните задание 1 для схемы, изображённой на рисунке 23.7.

О а) Составьте формулу, описывающую схему, изображённую на рисунке 23.8.

б) Упростите получившуюся формулу.

в) Составьте вентильную схему для получившейся формулы.

ху z

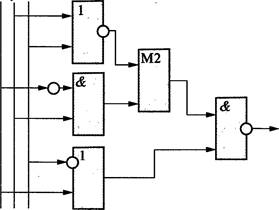
Рис. 23.9

Выполните задание 4 для схемы, изображённой на рисунке 23.9.

О Объясните, почему из вентилей И, ИЛИ, НЕ можно собрать схему, эквивалентную любому логическому элементу. (Совет: воспользуйтесь сведениями из п. 21.1.)

а) Можно ли из вентилей И и НЕ построить схему, эквивалентную вентилю ИЛИ? Ответ «да» подтвердите, указав такую схему, ответ «нет» обоснуйте.

6)* Можно ли из вентилей И и ИЛИ построить схему, эквивалентную вентилю НЕ? Ответ «да» подтвердите, указав такую схему, ответ «нет» обоснуйте.

О а) Составьте для логической функции f= (х -» у) (у х) таблицу значений. Какая функция из перечисленных в таблице на с. 144 эквивалентна функции f?

б) Выполните задание а для логической функции f=(x у) (у х).

в) Выполните задание а для логической функции

О а) Известно, что, используя только операцию Шеффера, можно построить схему, эквивалентную вентилю И. Нарисуйте схему, подтверждающую это утверждение.

б) Выполните задание, аналогичное заданию а, для вентилей ИЛИ и НЕ.

Вместе с утверждением, сформулированным в задании 6, полученные вами результаты показывают, что при конструировании логических элементов можно обойтись только операцией Шеффера.

Выполните для операции Пирса такие же задания, как 9а и 96. Какой вывод можно сделать?

О* Исследуйте, существуют ли такие логические элементы с двумя входами, отличные от операции Шеффера и операции Пирса, которые, подобно этим элементам, «в одиночку» могли бы реализовать любой логический элемент.

е* а) Постройте схему сумматора, вычисляющего сумму трёх однозначных чисел в двоичной системе. (Совет: составьте сначала таблицу значений младшего и старшего разрядов для суммы трёх однозначных чисел.)

б) При сложении многозначных чисел в старших разрядах приходится учитывать появление так называемой единицы переноса. Это означает, что в этих разрядах складываются не два однозначных числа, а три. Используя результат пункта а, постройте схему сумматора для сложения двух двузначных чисел в двоичной системе счисления.

Ответы и результат ы в ы числительн ы х экспериментов

5 2. 4. з.

S 3.1. 7. б) 2832. 11. в) 7. 17. а) х = 6, у = 5. 20. 6) 14.

 3.2. 5. 120. 11. а) 4096 и 32767.

 4. 8. г) коричневато-оранжевый (кирпичный). 9. г) сиреневый (или фиолетовый). 5 5. 1.

S 6.1. 15. а) 533. б)

. 11

(для большей наглядности нули заменены точками).

19.

           6.2. 10. 6)              13. 00.

9. 4. а) Население < 1000 И Блок = ЕЭС (если в ответе на этот запрос будет указано хотя бы одно государство, то ответ на вопрос, сформулированный в пункте а, отрицательный).

S 10. 9. а) влево; вниз; вправо. 10. б) 9. 12. 6) 10.

11. 5. 15; F3.

 12.1. 4. а) 12,51+ 24. 7. а) хз=-7; х4 = 27; = -1207.

	637	4937	51 983
Результат		4937	1091
	20	зоо	7000
Результат	71	1987	70 657

11. б)

12. б)

Ответы и результаты вычислительных экспериментов

а	6	о
	10	5
Координаты точки

16.   б)

17.   б) максимальное значение 420.

S 12.2. 4. а) 6; в) 12. 5. б) 8 + 18h, где — любое целое неотрицательное число; в) таких п не существует. 6. а) 2.

 12.3. 1. в) 2, 4, 6; г) -8, -7, -6, -5, -4, -2, -3, -2, -1, 2, з.

 13.2. 1. в) 143.

т	1	2	з	4	5	6
			9	26	8	18	26	36

 13.3. 2. а) 9. З.

2. а) 2. З. О при т < 5, 6 при т > 5. То же самое можно записать одной формулой З + З т — 4,5 / (т — 4,5).

S 13.4. 4. Третье число Кармайкла: 1729.

S И. 1. а) 6; б) 10; в) 24. З. а) 2, 5, 7, 16, 33, 65. З. а) -1, о, з, -12, 1, 5.

 15.1. 6. ж) А СЕ

I I I

BDF

 15.2. 1. в) СБВФ.

S 16. 10. б) Выигрышной стратегии нет ни у одного из игроков. Лучший результат, которого может добиться каждый из игроков, — ничья.

S 18. 2. д) Может. Вид последней амёбы всегда второй, независимо от того, как будут выбираться амёбы при исполнении тела цикла. З. а) массовый, N — любое целое число; б) не массовый; в) не массовый, единственное допустимое значение х — число О, для остальных значений х произойдёт остановка с ошибкой «извлечение корня из отрицательного числа»; г) массовый, А — любое неотрицательное число. 10. а) 11; б) ни разу. 5 21.1. 4. а) А = И, В=Л, С =И; 6) А = Л, В = И, С = И. S 21.2. 10. б) Зу S (у, у, х); в) Вг S (х, г, у).

11. б) Ву S (у, у, г) & S (у, г, х); д) Му Мг           (у, г, х).

15. а) Р (3, З, 3) = И; Р (5, 2, 6) = Л; Р (4, 4, 8) = Л;

Р (6, 9, 3) = И; Р (6, 9, 2) = Л; 6) 2=6; е) НОД (х, у).  & Z) (У &

          23. 1. а) (Х                  (Х У); в) Х + У.

Основная литература

Гейн А. Г. Информатика и ИКТ: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни / А. Г. Гейн, А. Б. Ливчак, А. И. Сенокосов, Н. А. Юнерман. — М.: Просвещение, 2008. —- 272 с.

Гейн А. Г. Информатика и ИКТ: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни / А. Г. Гейн, А. И. Сенокосов. — М.: Просвещение, 2009. 336 с.

Информатика. Задачник-практикум. В 2 т. / под ред. И. Г. Семакина, Е. К. Хеннера. Т. 1. — М.: ЛБ3, 1999.

Дополнительная литература

Алексеев А. В. Олимпиады школьников по информатике / А. В. Алексеев. — Красноярск: Кн. изд-во, 1995. 224 с.

Андреева Е. В. Математические основы информатики. Элективный курс: учеб. пособие / Е. В. Андреева, Л. Л. Босова, И. Н. Фалина. — М.: БИНОМ. Лаборатория знаний, 2005. — 328 с.

Андреева Е. В. Математические основы информатики. Элективный курс: метод. пособие / Е. В. Андреева, Л. Л. Босова, И. Н. Фалина. — М.: БИНОМ. Лаборатория знаний, 2007. — 312 с.

Андреева Е. В. Системы счисления и компьютерная арифметика / Е. В. Андреева, И. Н. Фалина. — М.: ЛБЗ, 2000. — 248 с.

Гейн А. Г. Информатика и информационные технологии: кн. для учителя: метод. рекомендации к учеб. 10 кл. / А. Г. Гейн. — М.: Просвещение, 2008. 160 с.

Гейн А. Г. Информатика и ИКТ: кн. для учителя: 11 класс / А. Г. Гейн, Н. А. Юнерман, А. А. Гейн. — М.: Просвещение, 2009. — 240 с.

Ефимова О. А. Практикум по компьютерной технологии: метод. пособие / О. А. Ефимова, М. В. Моисеева, Ю. А. Шафрин. — М.: АБФ, 1997. — 560 с.

Касаткин В. Н. Информация, алгоритмы, ЭВМ: пособие для учителя / В. Н. Касаткин. — М.: Просвещение, 1991. 192 с.

Кирюхин В. М. Информатика. Всероссийские олимпиады (Серия «Пять колец») / В. М. Кирюхин. — М.: Просвещение, 2009. 182 с.

Основная литература

Кольман Э.         Занимательная        логика / Э. Кольман, О. зих. — М.: Наука, 1966. — 127 с.

Матвеева Т. А. Информационная культура: учеб. пособие. Ч. 1 / Т. А. Матвеева, А. Г. Гейн, В. В. Мачульский и др. — Смоленск: Ассоциация XXI век, 2006. — 392 с.

Матвеева Т. А. Информационная культура: учеб. пособие. Ч. 2 / Т. А. Матвеева, А. Г. Гейн, В. В. Мачульский и др. — Смоленск: Ассоциация XXI век, 2007. — 416 с.

Окулов С. М. Задачи по программированию / С. М. Окулов, Т. В. Ашихмин, Н. А. Бушмелёва и др.: под ред. С. М. Окулова. — М.: БИНОМ. Лаборатория знаний, 2006. — 820 с.

Шауцукова Л. З. Информатика: 10—11 кл. : учеб. пособие для 10—11 кл. / Л. З. Шауцукова. — М.: Просвещение, 2004. — 143 С.

Шафрин Ю. А. Информационные технологии / Ю. А. Шафрин. — М.: Лаборатория Базовых Знаний, 1998. — 704 с.

Приложения

Таблица П.1

Основная часть ASCII

Двоичный код	Десятичный код	Символ	Двоичный код	Десятичный код	Символ
00100000	32	Пробел	00110111	55	7
00100001	33		00111000	56	8
00100010			00111001	57	9
00100011	35		00111010	58
00100100	36		00111011	59
00100101	37			60
00100110	38			61
00100111	39			62
00101000	40			63
00101001	41		01000000
00101010	42		01000001	65
00101011			01000010	66	В
00101100	44		01000011	67	с
00101101	45		01000100	68
00101110			01000101	69
	47		01000110	70
00110000	48	О	01000111	71
00110001	49	1	01001000	72	н
00110010	50	2	01001001	73
00110011	51	з	01001010	74
00110100	52	4	01001011	75
00110101	53	5	01001100	76
00110110	54	6	01001101	77	м