
Геометрический смысл производной.
Краткая теория.
Геометрический смысл производной связан с углом наклона касательной, проведенной к графику функции в данной точке или с угловым коэффициентом наклона касательной.
( Теория и разобранные примеры должны быть записаны в тетрадь)
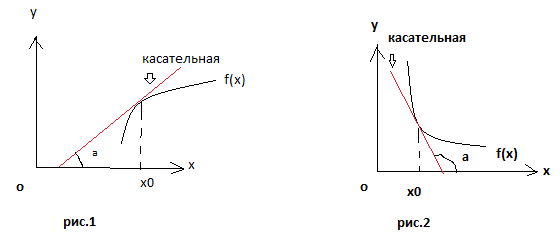
На рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а на рис.2 этот угол тупой. Если угол наклона касательной острый, то функция при увеличении значения переменной Х будет возрастать. Если угол наклона касательной тупой, как на рис.2, то функция на этом участке убывает.
Геометрический смысл производной:
1)f ´(x) = tgɑЗначение производной в заданной точке равно тангенсу угла наклона касательной, проведенной в заданной точке.
Или
2)f ´(x) =KЗначение производной в заданной точке равно угловому коэффициентуКнаклона касательной. (Так как касательная – это прямая линия, то ее уравнение имеет вид: y = k·x + b, где k =f ´ (x) )
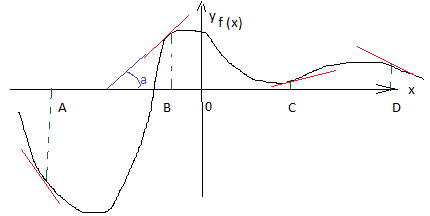
Пример1. На рисунке изображен график функции и касательные , проведенные к нему в точках с абсциссами A, B, C, D.
 В правом столбце
указаны значения производной функции в точках A, B, C, D.Пользуясь
графиком, поставьте в соответствие каждой точке значение производной функции в
ней.
В правом столбце
указаны значения производной функции в точках A, B, C, D.Пользуясь
графиком, поставьте в соответствие каждой точке значение производной функции в
ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
A |
1) – 1,8 |
|
B |
2) – 0,7 |
|
C |
3) 1,4 |
|
D |
4) 0,5 |
При решении заполните таблицу, расчерченную ниже, в которой для каждой точки укажите номер соответствующего значения производной.
|
A |
B |
C |
D |
|
|
|
|
|
(При записи ответа укажите полученное четырехзначное число).
Решение.
Пояснения к решению. Их можно в решении не писать только заполненную таблицу и ответ.(Пояснения даны для того, чтобы вы поняли, как решать такого типа задание).
Сначала определим знаки производной в каждой отмеченной точке. Для этого надо мысленно продолжить каждую касательную ( красная) до пересечения с осью ОХ ( как сделано синим цветом для точки B). Увидим, что в точке A угол наклона касательной будет тупой ( угол берем только с положительным направлением оси ОХ, куда указывает стрелка оси), в точке B этот угол острый, в точке С– острый, в точке D – тупой. Производная f ´(x) = tgɑЗначение производной в заданной точке равно тангенсу угла наклона касательной, проведенной в заданной точкеДля острых углов тангенс положительный, чем больше острый угол тем больше его тангенс.Для тупых углов тангенс отрицательный, чем больше тупой угол тем меньше значение его тангенса. В точках Bи С производная положительная, причем в т.Bострый угол больше , чем в т. С. Значит, в таблицу ответов под точкой B пишем цифру 3, под точкой С пишем цифру 4. В точках Aи D производная отрицательна, причем в т. А тупой угол больше, чем в т.D. В таблице ответов под точкой А пишем цифру1, под точкой D пишем цифру 2.
|
A |
B |
C |
D |
|
1 |
3 |
4 |
2 |
Ответ: 1342
Пример 2.
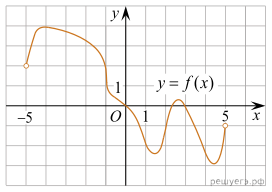 На рисунке изображен
график функции y = f(x), определенной на интервале
(−5; 5). Найдите количество точек, в которых касательная к графику
функции параллельна прямой y = 6 или совпадает
с ней.
На рисунке изображен
график функции y = f(x), определенной на интервале
(−5; 5). Найдите количество точек, в которых касательная к графику
функции параллельна прямой y = 6 или совпадает
с ней.
Решение. Поскольку касательная параллельна прямой y = 6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. У данной функции производная равна нулю только в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y = 6 или совпадает с ней в 4 точках.
Ответ: 4.
Пример 3.
, ,
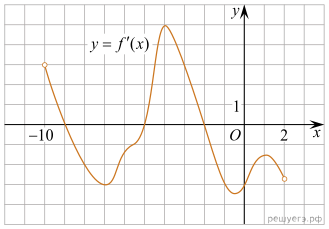 На рисунке изображен
график производной функции f(x), определенной на интервале
(−10; 2). Найдите количество точек, в которых касательная к графику
функции f(x) параллельна прямой y = −2x − 11
или совпадает с ней.
На рисунке изображен
график производной функции f(x), определенной на интервале
(−10; 2). Найдите количество точек, в которых касательная к графику
функции f(x) параллельна прямой y = −2x − 11
или совпадает с ней.
Решение. 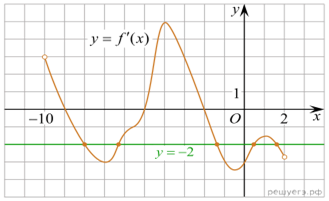 Значение производной в
точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой y = −2x − 11
или совпадает с ней, их угловые коэффициенты равны −2. Найдем количество
точек, в которых
Значение производной в
точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой y = −2x − 11
или совпадает с ней, их угловые коэффициенты равны −2. Найдем количество
точек, в которых ![]() это
соответствует количеству точек пересечения графика производной с прямой y = −2.
На данном интервале таких точек 5.
это
соответствует количеству точек пересечения графика производной с прямой y = −2.
На данном интервале таких точек 5.
Ответ: 5.
,
Пример 4.
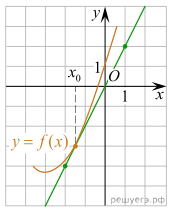 На рисунке изображён
график функции y=f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
На рисунке изображён
график функции y=f(x) и касательная к нему в точке с абсциссой x0.
Найдите значение производной функции f(x) в точке x0.
Решение. 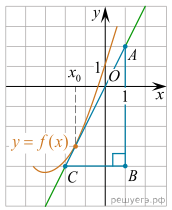 Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Построим
треугольник с вершинами в точках A (1; 2),
B (1; −4), C(−2; −4). Угол наклона касательной
к оси абсцисс будет равен углу ACB:
Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Построим
треугольник с вершинами в точках A (1; 2),
B (1; −4), C(−2; −4). Угол наклона касательной
к оси абсцисс будет равен углу ACB:
![]()
Ответ: 2.
Пример 5.
,
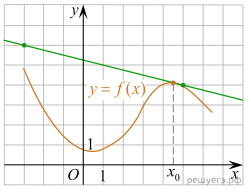 На рисунке изображены
график функции y = f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
На рисунке изображены
график функции y = f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
Решение. 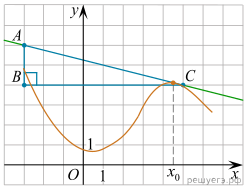 Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Построим
треугольник с вершинами в точках A (−3; 6), B (−3; 4),
C (5; 4). Угол наклона касательной к оси абсцисс будет равен
углу, смежному с углом ACB:
Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Построим
треугольник с вершинами в точках A (−3; 6), B (−3; 4),
C (5; 4). Угол наклона касательной к оси абсцисс будет равен
углу, смежному с углом ACB:
![]()
![]()
Ответ: −0,25.
Пример 6.
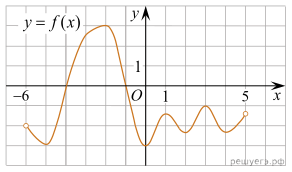 На рисунке изображен
график функции y = f(x), определенной на интервале
(−6; 5). Найдите количество точек, в которых касательная к графику
функции параллельна прямой y = −6.
На рисунке изображен
график функции y = f(x), определенной на интервале
(−6; 5). Найдите количество точек, в которых касательная к графику
функции параллельна прямой y = −6.
Решение. Касательная параллельна горизонтальной прямой в точках экстремумов, таких точек на графике 7.
Ответ: 7.
Пример 7.
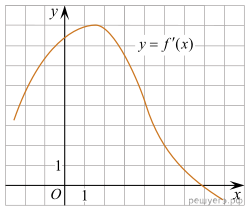 На рисунке изображен
график производной функции
На рисунке изображен
график производной функции ![]() Найдите абсциссу точки,
в которой касательная к графику
Найдите абсциссу точки,
в которой касательная к графику ![]() параллельна прямой
параллельна прямой ![]() или совпадает с ней.
или совпадает с ней.
Решение. 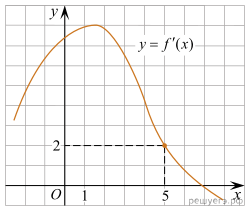 Значение производной в
точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой
Значение производной в
точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой ![]() или совпадает с ней,
она имеет угловой коэффициент равный 2 и
или совпадает с ней,
она имеет угловой коэффициент равный 2 и ![]() Осталось найти, при
каких x производная принимает значение 2. Искомая точка
Осталось найти, при
каких x производная принимает значение 2. Искомая точка ![]()
Ответ: 5.
Пример 8. Прямая ![]() параллельна касательной к графику функции
параллельна касательной к графику функции ![]() Найдите абсциссу точки касания.
Найдите абсциссу точки касания.
Решение. Значение производной в
точке касания равно угловому коэффициенту касательной. Поскольку касательная
параллельна прямой ![]() их угловые коэффициенты
равны. Поэтому абсцисса точки касания находится из уравнения
их угловые коэффициенты
равны. Поэтому абсцисса точки касания находится из уравнения ![]() :
:
![]()
Ответ: 0,5.
Пример 9. Прямая y = 3x
+ 1 является касательной к графику функции ![]() ax2 +
2x + 3. Найдите a.
ax2 +
2x + 3. Найдите a.
Решение. Прямая ![]() является касательной к графику функции
является касательной к графику функции ![]() в точке
в точке ![]() тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно ![]() и
и
![]() В нашем случае
имеем:
В нашем случае
имеем:
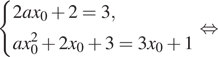
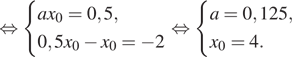
Искомое значение а равно 0,125.
Ответ: 0,125.
Пример 10. Прямая ![]() является касательной к графику функции
является касательной к графику функции ![]() Найдите b, учитывая, что абсцисса
точки касания больше 0.
Найдите b, учитывая, что абсцисса
точки касания больше 0.
Решение. Условие касания графика
функции ![]() и прямой
и прямой ![]() задаётся системой требований:
задаётся системой требований:
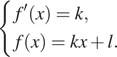
В нашем случае имеем:
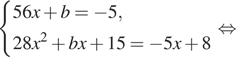
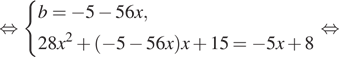
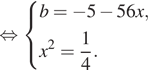
По условию абсцисса точки касания положительна, поэтому x = 0,5, откуда b = −33.
Пример 11.
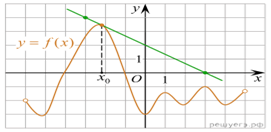 На рисунке изображены
график функции
На рисунке изображены
график функции ![]() и касательная к этому
графику, проведённая в точке x0. Найдите значение производной
функции g(x) = 6f(x)
− 3x в точке x0.
и касательная к этому
графику, проведённая в точке x0. Найдите значение производной
функции g(x) = 6f(x)
− 3x в точке x0.
Решение. 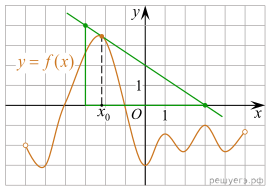 Найдём производную
функции g(x):
Найдём производную
функции g(x):
![]()
По рисунку найдём значение ![]() Значение производной
в точке касания равно угловому коэффициенту касательной, который, в свою
очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Поэтому
Значение производной
в точке касания равно угловому коэффициенту касательной, который, в свою
очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Поэтому ![]()
Тогда для искомого значения получаем
![]()
Ответ: −7
Пример
12.
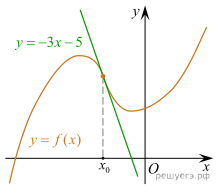
На рисунке изображены график функции ![]() и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение производной функции
и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение производной функции ![]() в
точке x0.
в
точке x0.
Решение. Найдём производную функции g(x):
![]()
Найдём значение ![]() Значение производной
в точке касания равно угловому коэффициенту касательной.
Значение производной
в точке касания равно угловому коэффициенту касательной.
![]()
Тогда искомое значение
![]()
Ответ: 42.
Пример 13.
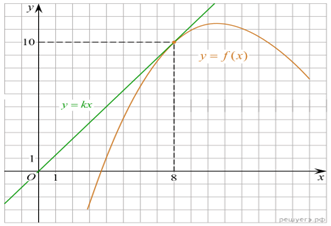
На рисунке изображен график функции y = f(x).
Прямая, проходящая через начало координат, касается графика этой функции в
точке с абсциссой 8. Найдите ![]()
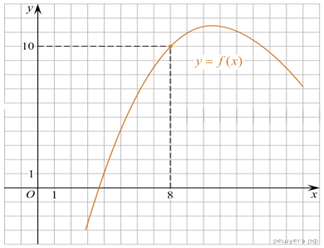
Решение. Поскольку касательная
проходит через начало координат, её уравнение имеет вид y = kx.
Эта прямая проходит через точку (8; 10), поэтому
10 = 8 · k, откуда k = 1,25.
Поскольку угловой коэффициент касательной равен значению производной в точке
касания, получаем: ![]()
Решить самостоятельно.
1.
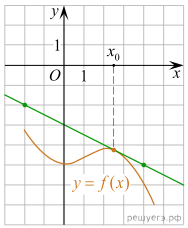 На рисунке изображены
график функции y = f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
На рисунке изображены
график функции y = f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
2.
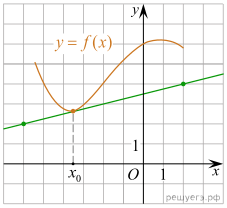
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
3.
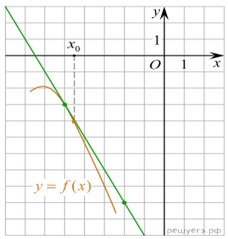
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
4.
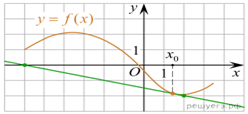 На рисунке изображён
график функции
На рисунке изображён
график функции ![]() и касательная к нему в
точке с абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
и касательная к нему в
точке с абсциссой x0. Найдите значение производной функции f(x)
в точке x0.
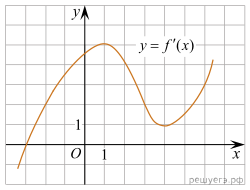
5. 
,
,
На рисунке изображен график производной функции ![]() Найдите абсциссу точки,
в которой касательная к графику
Найдите абсциссу точки,
в которой касательная к графику ![]() параллельна оси абсцисс
или совпадает с ней.
параллельна оси абсцисс
или совпадает с ней.
6. 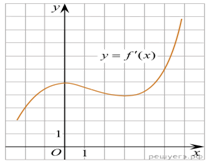
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
7.
,
, ,
,
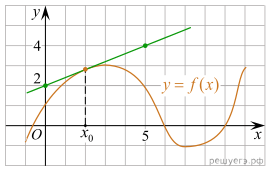 На рисунке изображены
график функции
На рисунке изображены
график функции ![]() и касательная к этому
графику, проведённая в точке
и касательная к этому
графику, проведённая в точке ![]() Найдите значение производной
функции
Найдите значение производной
функции ![]() в
точке x0.
в
точке x0.
8.
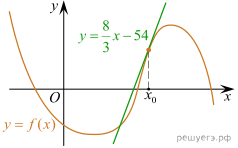 На рисунке изображены
график функции
На рисунке изображены
график функции ![]() и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение функции
и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение функции ![]() в
точке x0.
в
точке x0.
9.
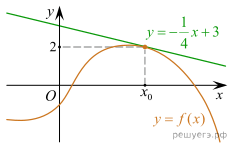 На рисунке изображены
график функции
На рисунке изображены
график функции ![]() и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение функции
и касательная к этому
графику, проведённая в точке x0. Уравнение касательной
показано на рисунке. Найдите значение функции ![]() в
точке x0.
в
точке x0.
10.
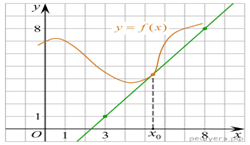
На рисунке изображены график функции ![]() и касательная к нему в
точке с абсциссой
и касательная к нему в
точке с абсциссой ![]() Найдите значение производной
функции
Найдите значение производной
функции ![]() в точке
в точке ![]()
4.
11.
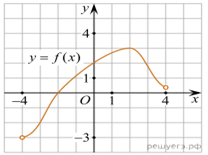 На рисунке изображён
график функции y = f(x),
определённой на интервале (−4; 4). Найдите корень уравнения f '(x) = 0.
На рисунке изображён
график функции y = f(x),
определённой на интервале (−4; 4). Найдите корень уравнения f '(x) = 0.
12.
На рисунке изображен график функции и касательные , проведенные к нему в точках с абсциссами A, B, C, D.
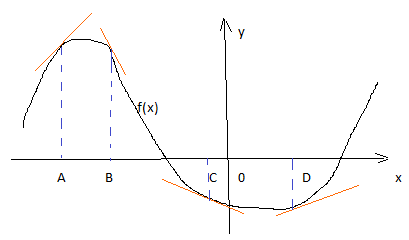 В
правом столбце указаны значения производной функции в точках A, B, C, D.Пользуясь графиком, поставьте в соответствие каждой
точке значение производной функции в ней.
В
правом столбце указаны значения производной функции в точках A, B, C, D.Пользуясь графиком, поставьте в соответствие каждой
точке значение производной функции в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
A |
1) - 0,5 |
|
B |
2) 1,7 |
|
C |
3) -2 |
|
D |
4) 0,6 |
|
A |
B |
C |
D |
При решении заполните таблицу, расчерченную ниже, в которой для каждой точки укажите номер соответствующего значения производной.
(При записи ответа укажите полученное четырехзначное число).
13.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
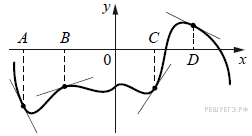
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
|
ТОЧКИ |
|
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
А) A Б) B В) C Г) D |
|
1) −0,5 2) −2 3) 1,5 4) 0,3 |
|
А |
Б |
В |
Г |
14.
Прямая, проходящая через начало координат, касается графика функции в точке М с координатами М( -2; 9). Найдите значение производной в точке х0 = -2
15.
Прямая, проходящая через начало координат, касается графика функции в точке А с координатами А ( -3,5; -10,5). Найдите значение производной в точке х0 = -3,5
https://znanio.ru/
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.