Хитрый приёмчик - хуманизация

Хитрый приёмчик - хуманизация

Не так давно появился новый модный иностранный термин – хуманизация, для которого существует синоним – очеловечивание неодушевленных предметов. Воспользуемся этим понятием, поскольку молодёжь лучше ориентируется в иностранных словах. А опытные учителя – энтузиасты давно и успешно пользуются данным методическим приёмом, особенно в начальной школе и в среднем звене, где на эмоциональном уровне игры и сказки способствуют лучшему усвоению сложного материала.

Приведу несколько примеров из своего опыта.

1. Видеоурок. Основное свойство дроби – https://youtu.be/AL-ZJJ7joyg

В этом ролике использовалась сказка «Простая дробь» из сборника Ф. Д. Кривина «Несерьёзные Архимеды». (М.: Молодая гвардия, 1971). Около 2 млн просмотров — значит, полезная находка для темы урока.

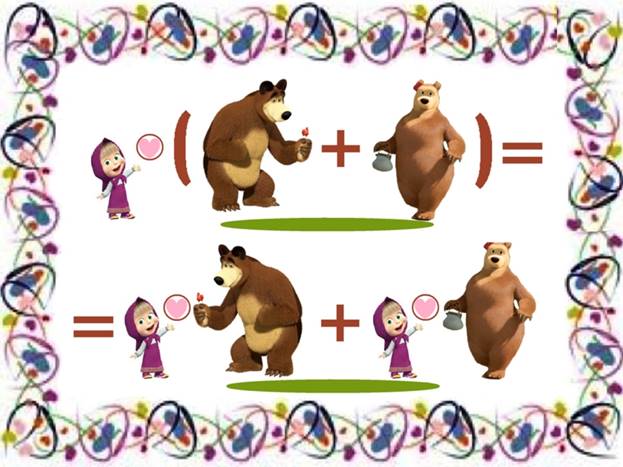
2. Раскрытие скобок по распределительному закону умножения.

Машенька, придя к медведям в гости, обязательно подарит своё сердечное приветствие и Мише, и медведице. Так и при раскрытии скобок внешний множитель добавляется к каждому слагаемому в скобках. Забыть добавить множитель, всё равно, что забыть поздороваться с кем-либо в доме. Это невежливо. И дети с удовольствием будут искать ошибки у отвечающего, вызванного к доске, чтобы уличить одноклассника в «невежливости». Это шуточная игра, но закон-то запоминается. А нужен он в алгебре вплоть до старших классов.

3. Противоположные числа и модуль.

Поскольку тема модуль следует почти сразу за темой противоположные числа, то у детей начинается путаница в голове. Чтобы сформировать навык (компетенцию) определения модуля и нахождения противоположных чисел можно воспользоваться картинками. Противоположные числа расположены напротив друг друга, на одном и том же расстоянии от нуля, но по разные стороны. Они отличаются знаком. И картинка задаёт некоторый антагонизм (мальчик-девочка, кошка-собака), чтобы запомнить, что противоположные числа имеют отличия. Модуль же всегда положителен, так как показывает расстояние от нуля до данного числа. Для запоминания этого понятия можно воспользоваться такой аллегорией: модуль – это разбойник-уравнитель. Он приходит к числам и отбирает у них знаки. Положительное число пишут без знака. После взятия модуля оно остаётся таким же. Как и ноль, у которого вообще знака нет. Отрицательное число после взятия модуля тоже остаётся без знака. Поэтому понятно, почему в уравнении |х| = 5,  х могло быть как +5, так и –5.

Может возникнуть вопрос, где брать такие картинки? Можно предложить детям проиллюстрировать запоминалочки самостоятельно. Это тоже поспособствует лучшему запоминанию информации.

А я делаю коллажи из того, что находится в Интернете в свободном доступе.

Скачано с www.znanio.ru