Курс: Информатика                                     

ЛЕКЦИЯ №4

Тема: Информационная мера Шеннона

1. ИНФОРМАЦИОННАЯ МЕРА ШЕННОНА

1.1. Количество информации и избыточность

1.2. Энтропия непрерывных сообщений

2. УСЛОВНАЯ ЭНТРОПИЯ И ВЗАИМНАЯ ИНФОРМАЦИЯ

2.1. Дисктретные системы передачи информации

2.2.          Непрерывные системы передачи информации

Слайды к лекции №4

1. Условная энтропия и взаимная информация.

2. Количество информации и избыточность

3. Аддитивность информационной меры

Лекция №4

Тема: ИНФОРМАЦИОННАЯ МЕРА ШЕННОНА.

         1. ИНФОРМАЦИОННАЯ МЕРА ШЕННОНА.

         1.1.  Количество информации и избыточность.

         Дискретные системы связи - системы, в которых как реализации сообщения, так и реализации сигнала представляют собой последовательности символов алфавита, содержащего конечное число элементарных символов. 

         Пусть  и  - случайные величины с множествами возможных значений  

         Количество информации  при наблюдении случайной величины  с распределением вероятностей задается формулой Шеннона:

         Единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения.

         При равномерном распределении  количество информации задается формулой Хартли:

.

         Справедливы следующие соотношения:

         1)

         2)  

         3)  если  и  - независимы.

         Избыточностью называется

         Рассмотрим примеры.

            Пример 1. Имеются два источника информации, алфавиты и распределения вероятностей которых заданы матрицами:

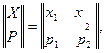
         Определить, какой источник дает большее количество информации, если

1)  2)

         Решение. Для первого источника при равновероятном распределении воспользуемся формулой Хартли. Для  и  имеем

         Следовательно, источник с тремя символами дает большее количество информации. Для второго случая воспользуемся формулой Шеннона:

 с учетом условия задачи имеем

С другой стороны,

Поскольку

   то

         Пример 2. Источник сообщений выдает символы из алфавита   с вероятностями     Найти количество информации и избыточность.

         Решение. По формуле Шеннона

(бит).

По определению избыточности

1.2. Энтропия непрерывных сообщений

         Непрерывные системы передачи информации - системы, в которых как реализации сообщения, так и реализации сигнала на конечном временном интервале  представляют собой некоторые непрерывные функции времени.

         Пусть  - реализации непрерывного сообщения на входе какого-либо блока схемы связи,  - реализация выходного сообщения (сигнала),  - плотность вероятности ансамбля входных сообщений,  - плотность вероятности ансамбля выходных сообщений

         Формулы для энтропии  непрерывных сообщений получаются путем обобщения формул для энтропии дискретных сообщений. Если  - интервал квантования (точность измерения), то при достаточно малом  энтропия непрерывных сообщений

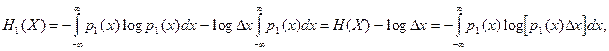
где 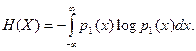 По аналогии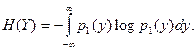

         Пример 1. По линии связи передаются непрерывные амплитудно-модулированные сигналы  распределенные по нормальному закону с математическим ожиданием  и дисперсией

         Определить энтропию  сигнала при точности его измерения  

         Решение. По условию плотность вероятности сигнала

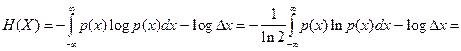
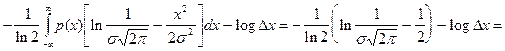
         Подставляя числовые значения, получаем

 дв. ед.

2. УСЛОВНАЯ ЭНТРОПИЯ И ВЗАИМНАЯ ИНФОРМАЦИЯ

         2.1. Дисктретные системы передачи информации.

         Условной энтропией величины  при наблюдении величины  называется

         Справедливы соотношения:

         Взаимной информацией величин  и  называется

         Справедливы следующие соотношения:

         Если  и независимы, то =0.

         При расчетах условной энтропии и взаимной информации удобно пользоваться следующими соотношениями теории вероятностей:

         1) теорема умножения вероятностей ;

         2) формула полной вероятности  

         3) формула Байеса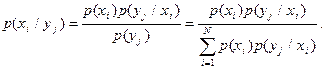

         Рассмотрим пример.

         Пример 1. Дана матрица

,  .

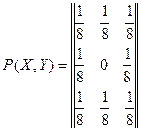         Определить:      

         Решение. По формуле полной вероятности имеем:  

         Следовательно,

         По теореме умножения

         Следовательно,

         Аналогично

2.2. Непрерывные системы передачи информации.

         Пусть  - реализации непрерывного сообщения на входе какого-либо блока схемы связи,  - реализация выходного сообщения (сигнала),  - одномерная плотность вероятности ансамбля входных сообщений,  - одномерная плотность вероятности ансамбля выходных сообщений,  - совместная плотность вероятности,  - условная плотность вероятности

при известном  Тогда для количества информации  справедливы следующие соотношения:

,

Здесь  - взаимная информация между каким-либо значением входного и значением выходного сообщений,   - средние значения условной информации,  - полная средняя взаимная информация.

         Условная энтропия определяется по формуле: 

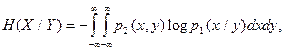
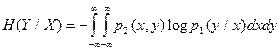
Когда  и  статистически связаны между собой, то

При независимых  и

Полная средняя взаимная информация определяется формулой:

         Рассмотрим пример.

         Пример 1. На вход приемного устройства воздействует колебание  где сигнал  и помеха  - независимые гауссовские случайные процессы с нулевыми математическими ожиданиями и дисперсиями, равными соответственно  и

         Определить: 1) количество взаимной информации  которое содержится в каком-либо значении принятого колебания  о значении сигнала  2) полную среднюю взаимную информацию

         Решение. По условию задачи  представляет собой сумму независимых колебаний  и  которые имеют нормальные плотности вероятности. Поэтому

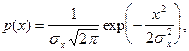
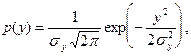
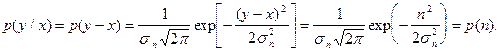
         1. Количество информации определяется по формуле:

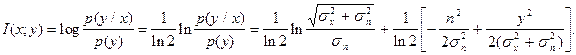
         2. Полная средняя взаимная информация:

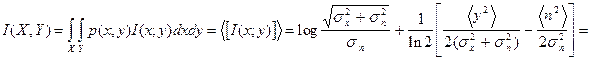
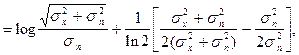
где  - знак усреднения по множеству.

         Таким образом,

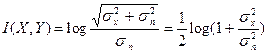 дв. ед.