Инновационные технологии на уроках

математики

 

Сравнительные особенности традиционной и инновационной педагогики Характеристики образовательных моделей

 

Особенности	Традиционная	Инновационная
Цель	Формирование знаний, умений и навыков	Развитие личности
Преобладающий тип и характер взаимоотношений	Субъект - объектный	Субъект - субъектный
Характер и стиль взаимодействия	Авторитарность, монологичность, закрытость	Демократичность, диалогичность, открытость, рефлексивность
Формы организации	Фронтальные, индивидуальные	Групповые, коллективные
Методы обучения	Иллюстративнообъяснительные, информационные	Проблемные: проблемного изложения, частично-поисковый, эвристический, исследовательский
Способы усвоения	Заучивание, деятельность по алгоритму	Поисковая, мыслительная деятельность, рефлексия
Функции учителя	Носитель информации, хранитель норм и традиций, пропагандист предметно-дисциплинарных знаний	Организатор сотрудничества, консультант, управляющий поисковой работой учащихся
Позиция ученика	Пассивность, отсутствие интереса, отсутствие мотива к личному росту	Активность, наличие мотива к самосовершенствованию, наличие интереса к деятельности

 

 

АКТИВНЫЕ МЕТОДЫ ОБУЧЕНИЯ –  

методы, стимулирующие познавательную деятельность обучающихся

 Строятся в основном на диалоге, предполагающем свободный обмен мнениями о путях разрешения той или иной проблемы. АМО характеризуются высоким уровнем активности учащихся. Возможности различных методов обучения в смысле активизации учебной и учебнопроизводственной деятельности различны, они зависят от природы и содержания соответствующего метода, способов их использования, мастерства педагога. Каждый метод активным делает тот, кто его применяет.

 

 

 

 

Игра «Художник»

№1

•     На доске записаны координаты точек (можно приготовить несколько вариантов для групповой работы): 

•     (0;12),(4;10),(0;10),(6;7),(0;7),(7;4),(1;4),(1;1),(-1;1),(-1;4),(-7;4),(0;7),(6;7),(0;10),(-4;10),(0;12).

•     Отметить на координатной плоскости каждую точку и соединить с предыдущей отрезком. Результат – определенный рисунок.

•     Выигрывает тот (или та команда), кто быстрее нарисует.

•     Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок и записать координаты вершин

№2

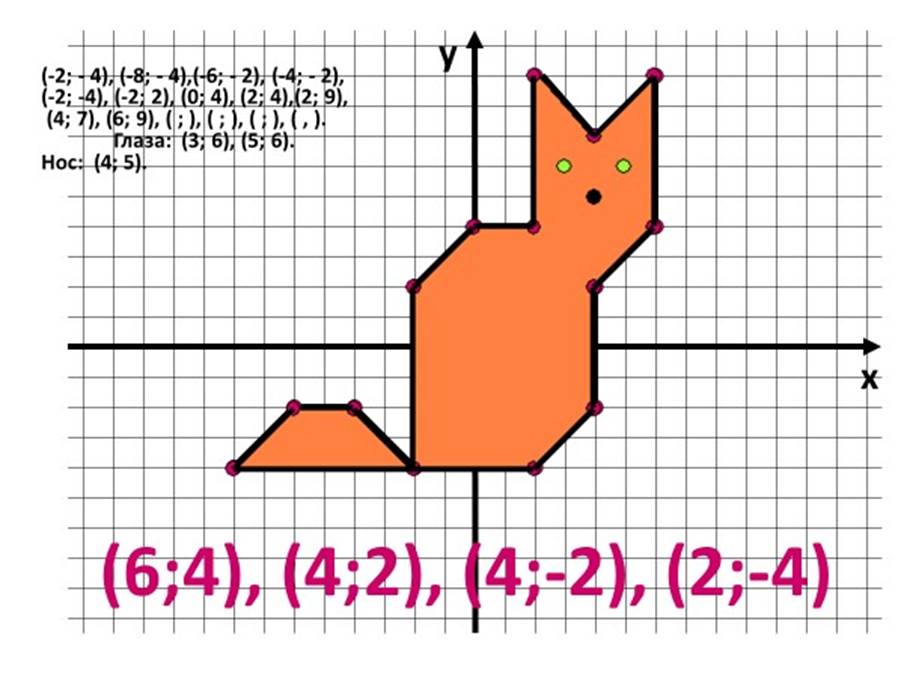
Построить фигурку кошки по координатам

(-2; - 4), (-8; - 4), (-6; - 2), (-4; - 2),  (-2; -4), (-2; 2), (0; 4), (2; 4), (-2; 9),  (4; 7), (6; 9), ( ; ), ( ; ), ( ; ), ( , ).

   Глаза:  (3; 6), (5; 6). Нос:  (4; 5).  

Достроить  фигурку кошки, предварительно решив  уравнения. Корни уравнений I варианта являются абсциссами, а корни уравнений  II варианта – ординатами искомых точек.   

КООРДИНАТА Х                        

 1. 4(х-2)=16          2.  2(3+2х)=4(3-х)+26                                     

3. –4(7-х)=х-16      4. 3х+7=8х-3

КООРДИНАТА У                           

1.6(у-1)=18                  2. 4(3-у)-11=7(2у-5)                     

3. 3(4у+8)=3у+6          4. 4у-13=9у+7  

 

Координата     х            Координата    у

 

х  = 6                                 у = 4     

х  = 4                                у = 2    

 

 х =4                                 у = -2 

 х  = 2                               у = -4    

 

 

 (6;4), (4;2), (4;-2), (2;-4)  

 

 

 

 

 

Игра « ДА»- «НЕТ»

 

•      В качестве закрепления нового материала успешно применяется игра «Да» - «Нет». Вопрос читается один раз, переспрашивать нельзя, за время чтения вопроса необходимо записать ответ «да» или «нет». Главное здесь – приобщить даже самых пассивных к учёбе.

•      Например, на уроке математики в 5 классе по теме: «Треугольник. Свойство углов треугольника».

•      Сумма острых углов треугольника равна 180 градусам?

•      Треугольник имеет  2 тупых угла?

•      Угол равностороннего треугольника равен 70 градусам?

•      Может ли треугольник, в котором два угла 40 и 60 градусов , быть тупоугольным?

•      Может ли треугольник с градусными мерами углов 10 и 20 быть остроугольным?

•      Может  ли треугольник иметь стороны 5,8,22?

•      Утверждения, с которыми либо соглашаются, либо не соглашаются, ученики готовят сами в качестве дополнения к домашнему заданию на протяжении изучения всей темы.  

 

 

Веб-квест –  

- это сайт в Интернете, с которым работают участники проекта, выполняя ту или иную  учебную задачу. В основе веб-квеста лежит индивидуальная или групповая работа  (часто с распределением ролей) по решению заданной проблемы с использованием интернет-ресурсов, подготовленных автором- модератором проекта.

Веб-квест - это пример организации интерактивной образовательной среды

 

 

 

Задания Веб-квеста «Выберись из комнаты»  

https://www.learnis.ru/323912/  Подготовила методист по математике ГБУДОПО «Псковский областной центр развития одарённых детей и юношества» Богданова Э.В.

 

 

1.     У профессора Альбуса Дамбалдора обучаются 29 юных волшебников. Из них 15 уже умеют отбивать заклинания, а 21 передвигать предметы с помощью волшебной палочки. Сколько юных волшебников умеют делать и то, и другое, если известно, что среди учеников Альбуса Дамбалдора только Рон Уизли ещё не научился ни тому, ни другому?

2.     Клетчатый квадрат 2×2 со стороной клетки в одну спичку складывается       из 12 спичек    (см. рисунок). А сколько спичек уйдёт на клетчатый квадрат     20×20?

3.     Бабушка печет блины. Когда в тарелке было 17 блинов, пришёл внучек из школы. Как только внук съедает три блина, бабушка подкладывает на тарелку ещё два. Маленький обжора ушёл в тот момент, когда на тарелке впервые стало ровно 11 блинов. Сколько блинов он съел?

4.     Вася задумал целое число. Коля умножил его не то на 5, не то на 6. Женя прибавил к результату Коли не то 5, не то 6. Саша отнял от результата Жени не то 5, не то 6. В итоге получилось 73. Какое число задумал Вася?

5.     В ряд высадил 12 ёлочек. Затем между каждыми двумя посаженными ёлочками посадили ещё по одной ёлочке. Затем эту операцию проделали ещё три раза. Сколько всего ёлочек посажено?

Ответы: 1.   8    2.   840 3.  12  4.   12   5.  177

 Набрав верную последовательность ответов 88401212177 обучающиеся, смогут выбраться из комнаты.

Кейс – технология

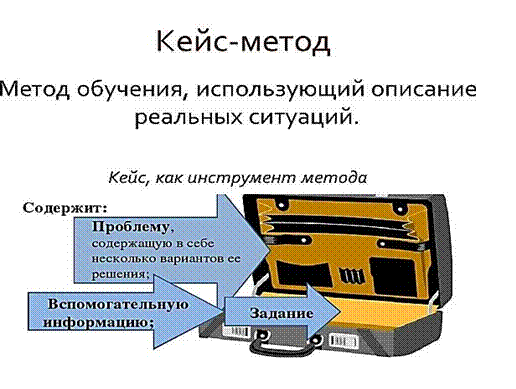
- одна из современных образовательных технологий, способствующая развитию умения анализировать жизненные ситуации, оценивать альтернативы, выбирать оптимальный вариант и планировать его осуществление.  

 «Кейс-метод» - это метод обучения, в рамках которого обучающиеся приобретают опыт использования математических знаний на практике посредством анализа и решения различных ситуаций.

 

Кейс «Многогранники вокруг нас»

Разработан  учителем математики 1 квалификационной категории «МОУ Тат.Каргалинская СОШ» Даутовой Г.А.

 

 

Тип кейса −исследовательский

1. Подготовительный этап

•      Вступительное слово

•      Цели

2. Ознакомительный этап.

2.1.        Введение

Сегодня на уроке мы поговорим о многогранниках, а точнее о      том, где встречаются многогранники в природе. А также услышим мнения ученых древности об использовании многогранников

2.2.        Описание ситуации

Интерес к многогранникам человек проявляет на протяжении всей своей  сознательной жизни – и малым ребенком, играющим  деревянными  кубиками, и    зрелым математиком.  

•      Как много существует правильных многогранников?

•      Почему пчелы строят соты именно так?

•      Создания природы красивы и симметричны. Свойства многогранников – это неотделимое свойство природной гармонии?

•      Идеи Пифагора, Платона, И.Кеплера о связи правильных  многогранников с гармоничным устройством в интересной научной  гипотезе.

2.3.                          Информационный материал

•      Литература Web – ресурсы

 

 

3.                                               Основной (аналитический) этап

        3.1.    Раунды:

1)вступительное слово учителя; распределение учащихся по группам (4-5 человек в каждой); организация работы групп:

краткое изложение членами групп прочитанных материалов и их обсуждение; выявление проблемных моментов; определение докладчиков;

2)    первый раунд дискуссии — обсуждение проблемных моментов в малых группах, поиск аргументов и решений; Работа над  защитой   рефератов по группам.

3)    второй раунд дискуссии — предоставление результатов анализа, общегрупповая дискуссия, подведение итогов дискуссии и найденных решений. Презентация всех групп результатов работы над гипотезой. 3.2.       Указания по проведению анализа конкретной  ситуации «Многогранники вокруг нас»

После знакомства учащихся с предоставленными фактами начинается их анализ в групповой работе. Этот процесс выработки решения, составляющий сущность метода, имеет временные рамки, которые определяет учитель.

Продуктивность групповой аналитической работы обеспечивается путем следования определенному алгоритму техники анализа «Гипотеза»:

•      Возникновение проблемной ситуации.

•      Осознание сущности затруднения и постановка проблемы.

•      Нахождение способа решения путем догадки или предположений и обоснование гипотезы.

•      Доказательство гипотезы.

•      Проверка правильности решения проблем.

4.               Итоговый этап

Заключительная презентация результатов аналитической работы (учащиеся могут узнать и сравнить несколько вариантов решений одной проблемы); обобщающее выступление учителя - анализ ситуации; оценивание учителем учащихся.

 

 

 

 

 

 

 

Кластер

 

– это способ графической организации материала, позволяющий сделать наглядными те мыслительные процессы, которые происходят при погружении в ту или иную тему.

В центре листа записывают ключевое понятие, а от него рисуют стрелы- лучи в разные стороны, которые связывают одно слово с другими, от которых в свою очередь лучи расходятся дальше и дальше.

Работа с кластерами

•      Составление нового;

•      Составление краткого рассказа по готовому кластеру;

•      Коррекция и совершенствование готового кластера;

•      Анализ и завершение неполного кластера;

•      Без указания главного термина, с которого начинается кластер, и определение  этого термина; • Без указания одного или нескольких терминов кластера и определение этих терминов.

 

 

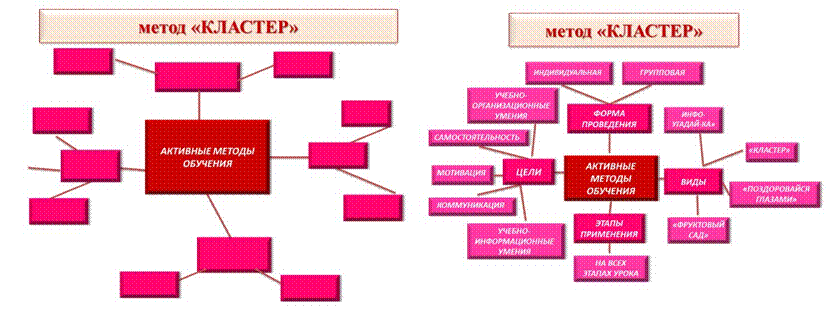
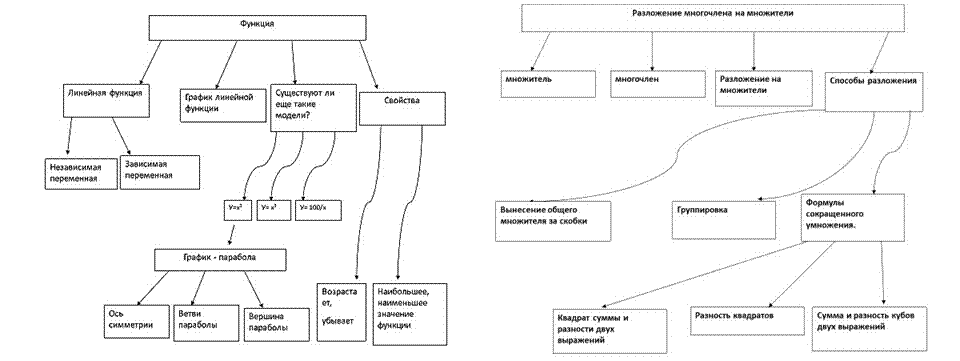
Примеры математических кластеров

 

 

 

 

 

 

 

 

 

 

 

Синквейн

 – это стихотворение, состоящее из пяти нерифмованных строк, составленное по правилу

 

 

 

 

 

 

 

 

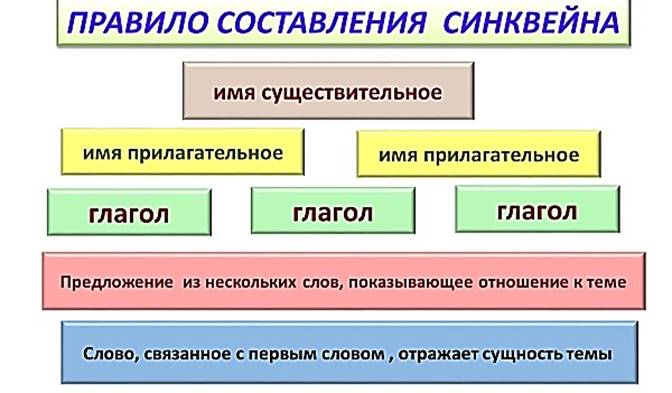
Примеры математических синквейнов

•      Линейная функция

•      Убывающая, возрастающая

•      Чертим, находим, определяем

•      Функции нужны в математике

•      Зависимость

 

 

•      Теорема

•      Прямая, обратная.

•      Доказывать, изучать, запоминать.

•      Развивает логическое мышление.

•      Трудно!

 

 

•      Степень

•      Понятная, лёгкая.

•      Решать, вычислять, считать.

•      Произведение нескольких множителей.

•      Интересно

 

 

 

 

Игра «Математическое лото. Пазлы»

 

•      Игра используется на уроках закрепления изученного материала, повторения или проверки знаний. Можно работать как в группах, так и индивидуально. Для игры изготавливаются несколько комплектов карточек с заданиями и ответами к ним. Ответы наносятся на карточках с любым изображением (репродукции известных картин, достопримечательности Родного края, памятники архитектуры, животные, растения и т.д.)

•      Учащиеся, решая задания, накрывают ответами соответствующий пример. Если все выполнено правильно, то они получают определенное изображение, что позволяет тут же проверить правильность решения.

•      Используя различные по содержанию изображения, игра дает возможность осуществить связь математики с другими предметами (краеведение, биология, история и др.)

 

 

 

 

 

 

Эссе

 

Смысл этого приема можно выразить следующими словами: “Я пишу для того, чтобы понять, что я знаю, что я думаю”. Это свободное письмо на заданную тему, в котором ценится самостоятельность, проявление         индивидуальности,        дискуссионность,     оригинальность      решения проблемы, аргументации.  

Примерные темы эссе:

«Математика вокруг нас»

«История математики»

«Зачем мне нужна математика» …

 

 

 

Описанные выше приемы позволяют:

 

▪  Актуализировать имеющиеся знания;

▪  Пробудить интерес к получению новой информации;

▪  Осуществить непосредственный контакт с новой информацией; ▪ Формировать творческий потенциал школьника; ▪ Формировать навыки работы с информацией.